2.Формула Ньютона-Лейбница.

Теорема. Если функция f(x) непрерывна на отрезке [а; в] и F(х) – первообразная функция f (x) на этом отрезке, то = F(в)- F(а) (1)

Формула (1) называется формулой Ньютона-Лейбница. Эта формула дает удобное правило вычисления определенного интеграла. Кроме того, она устанавливает связь между определенным и неопределенным интегралами.

3. Свойства определенного интеграла.

Пусть f(x) – функция, непрерывная на отрезке [а; в]. По определению полагаем: =0

1) Постоянный множитель можно выносить за знак определенного интеграла = .

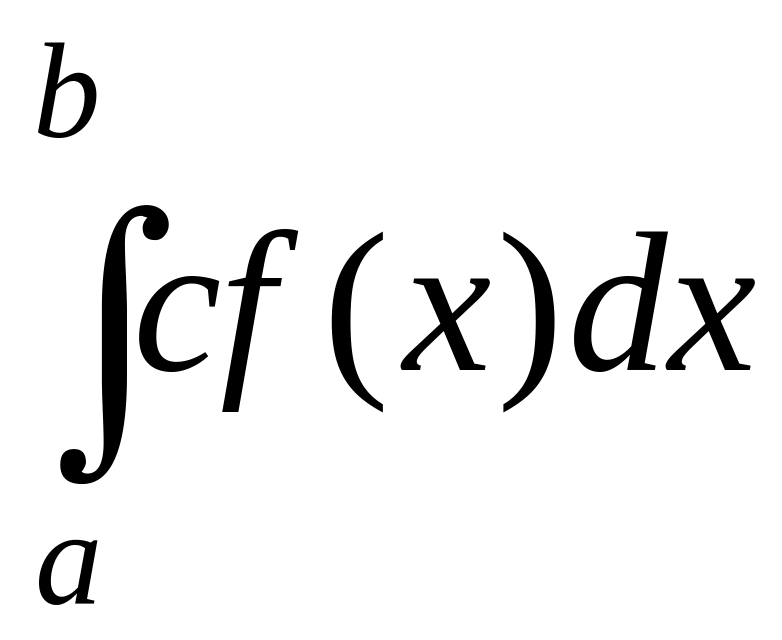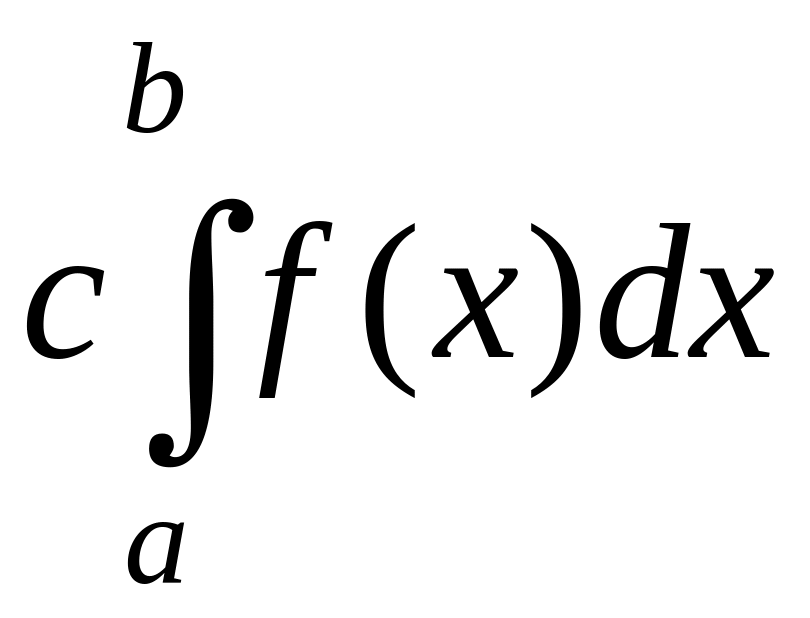2) Определенный интеграл от суммы двух функций равен сумме определенных интегралов от этих функций

= +

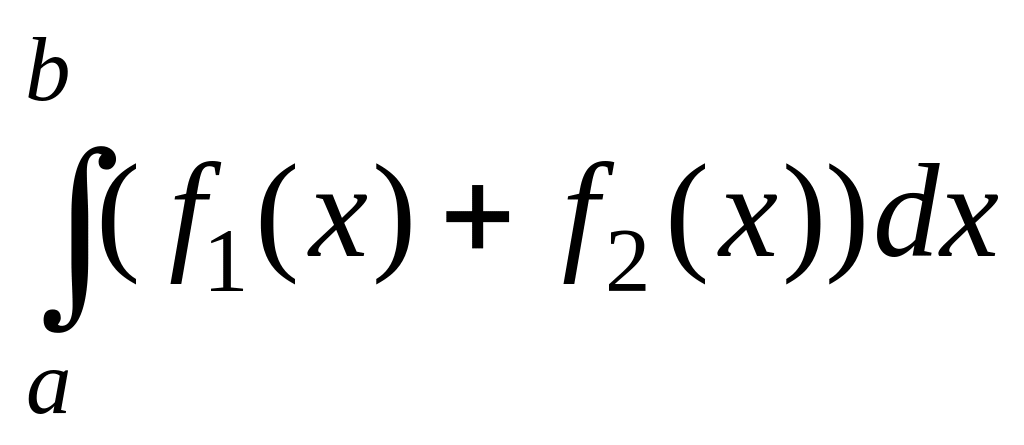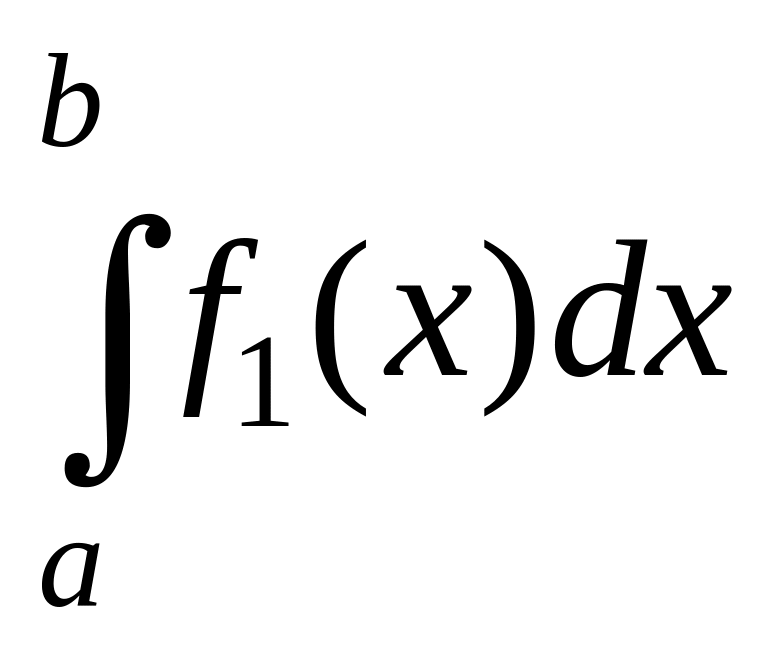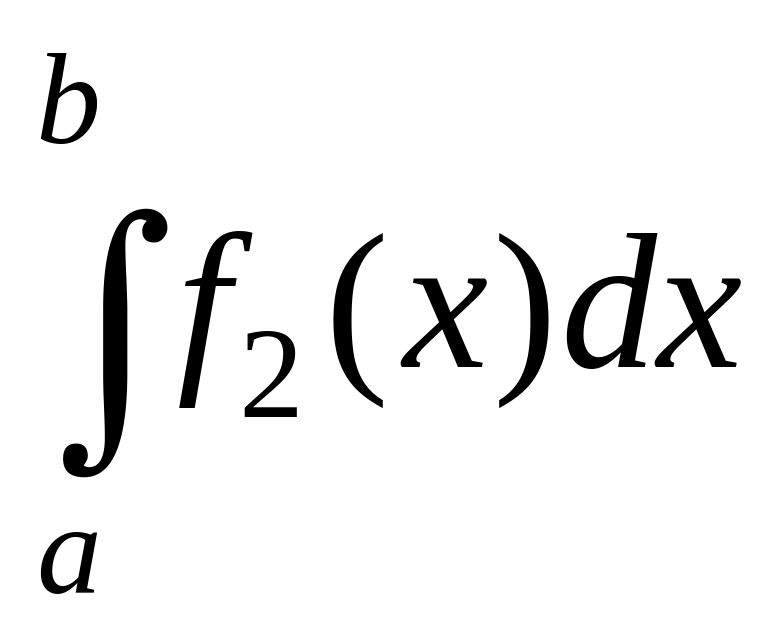
3) При перестановке пределов интегралов определенный интеграл меняет знак на противоположный

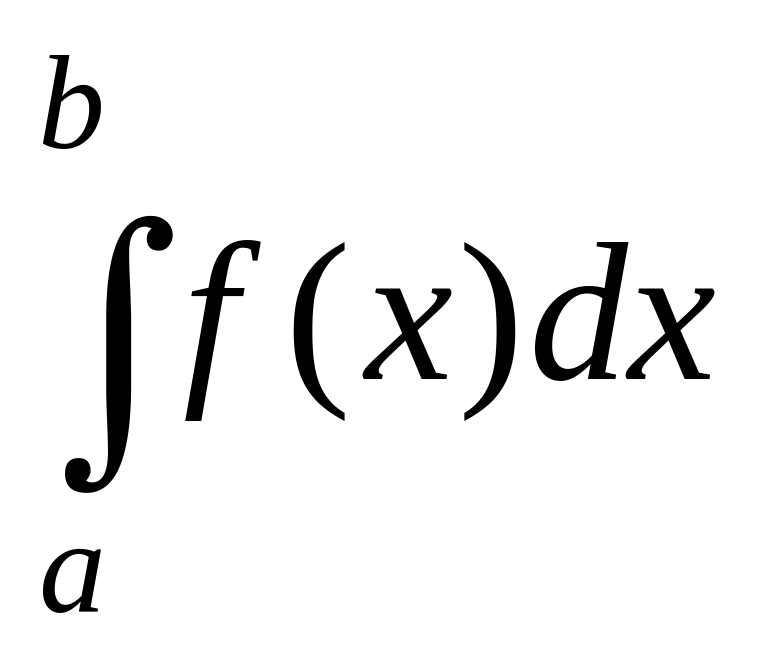
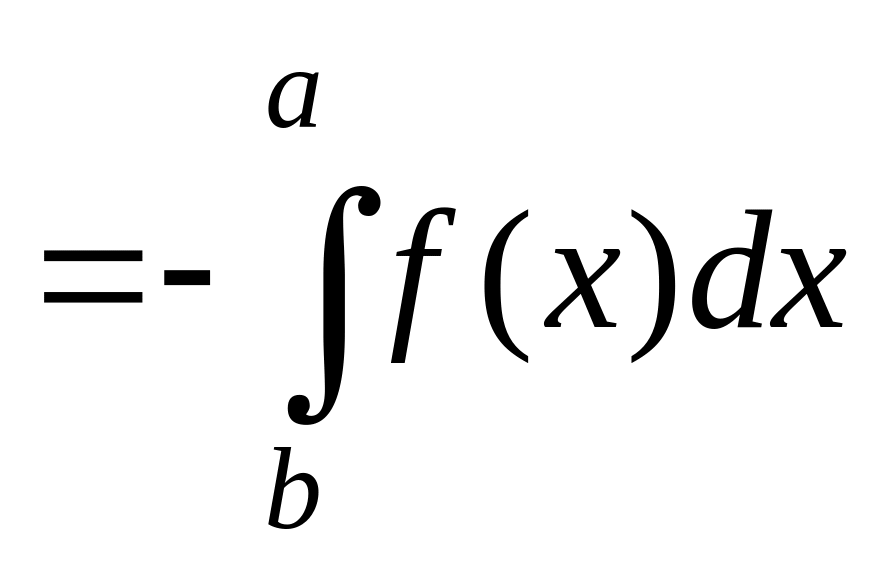
4) Интеграл по отрезку равен сумме интегралов по его частям:

,

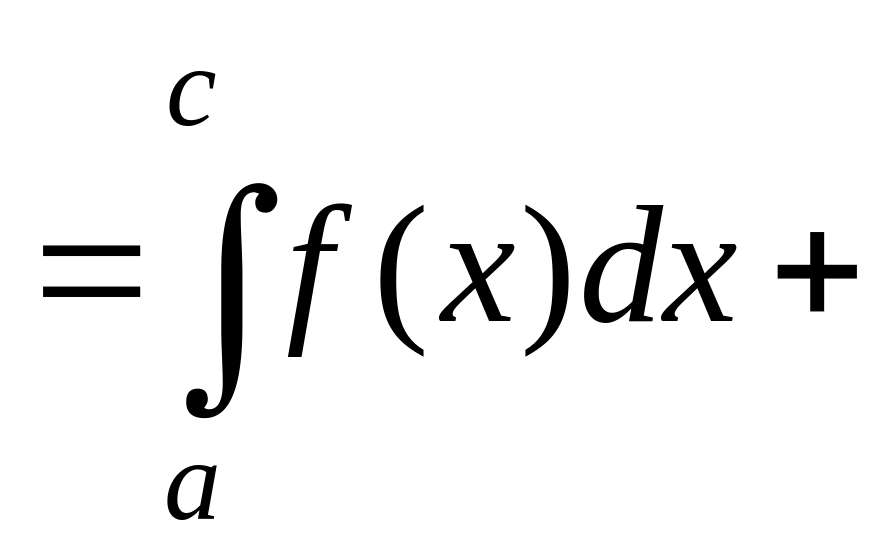
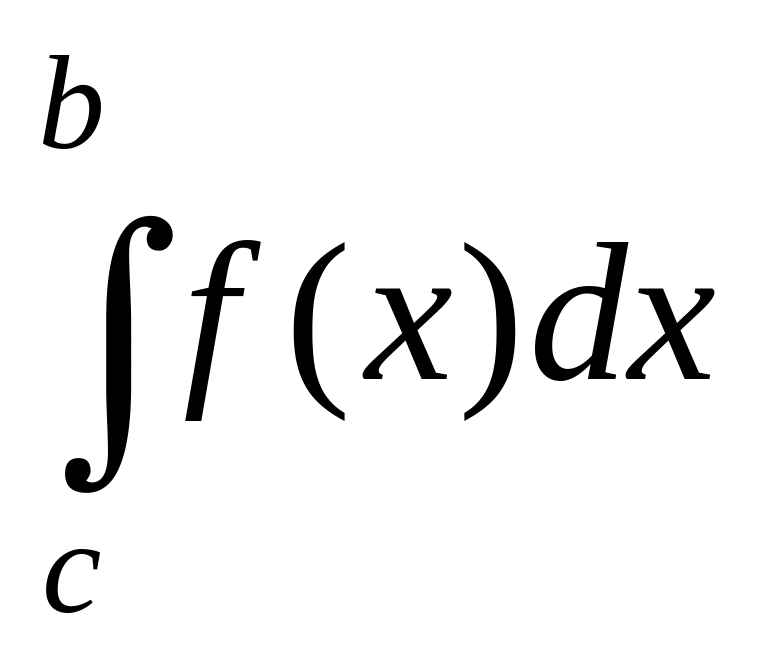где асв

Примеры 1) =2 =2 =1²-0²=1.

2) 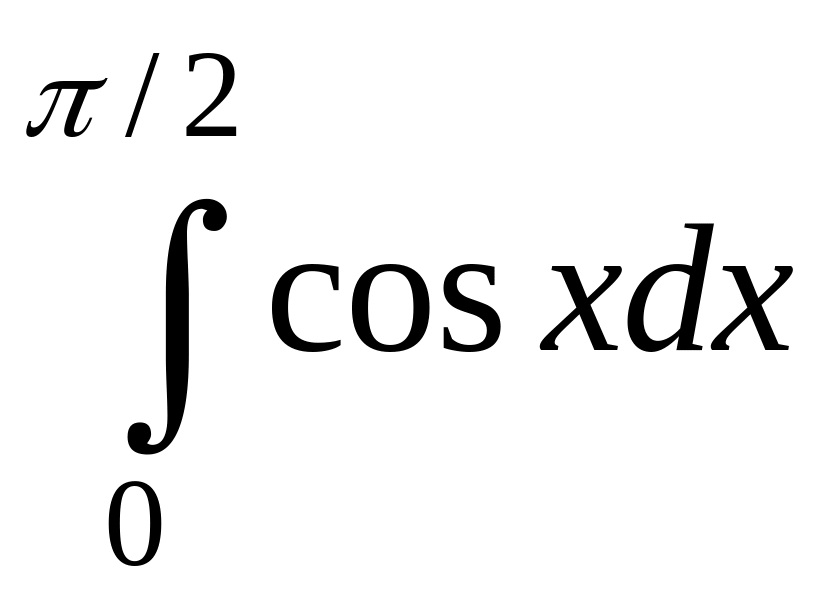= =sin -sin0=1.

§7. Вычисление площадей плоских фигур

Пусть f(x) непрерывна на отрезке [а;b]. Если f(x) 0 на [а;b], то площадь криволинейной трапеции, ограниченной линиями , у =f(x), у=0, х=a, х=b равна:

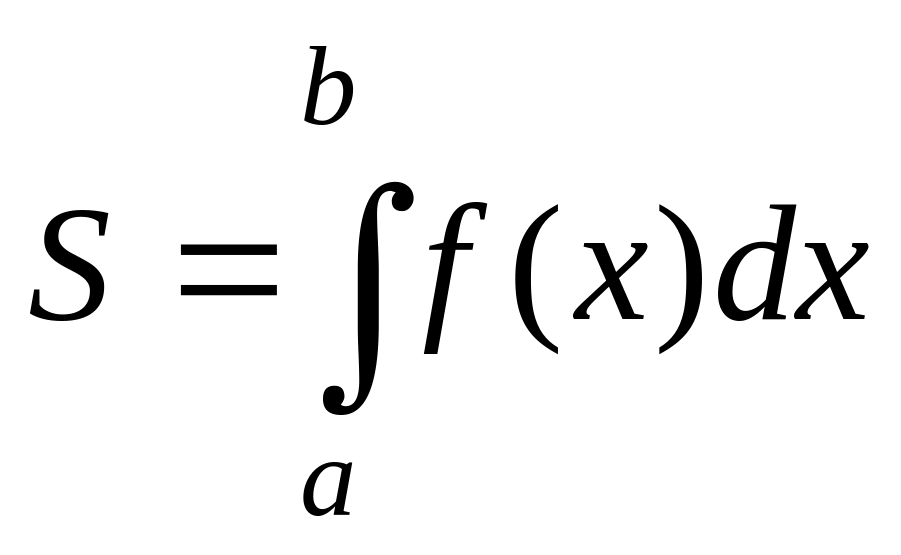(1)

Если f(x)0 на [а;b], то f(x)0 на [а;b] и 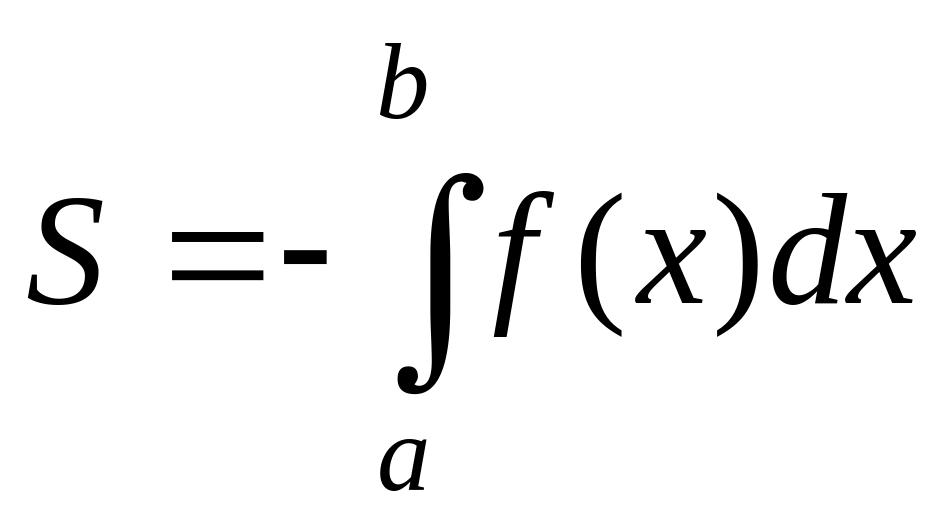или

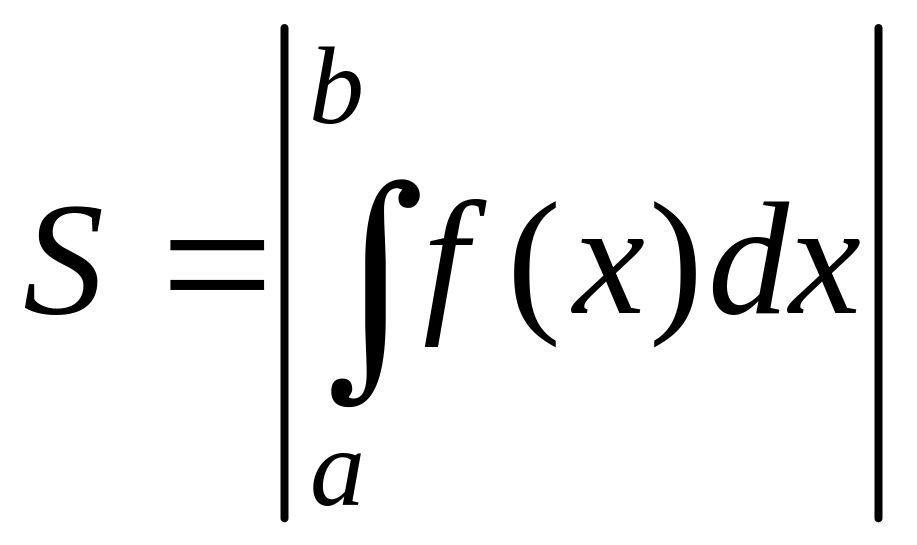(2)

Если, наконец, кривая у=f(x) пересекает ось Ох, то отрезок [а;b] надо разбить на части, в которых f(x) не меняет знака и в каждой такой части применить ту из формул (1) или (2), которая ей соответствует.

П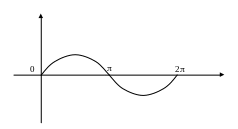 ример. Вычислить площадь фигуры, ограниченной линиями :y=sinx, х[0; 2], у=0.

Решение.

S=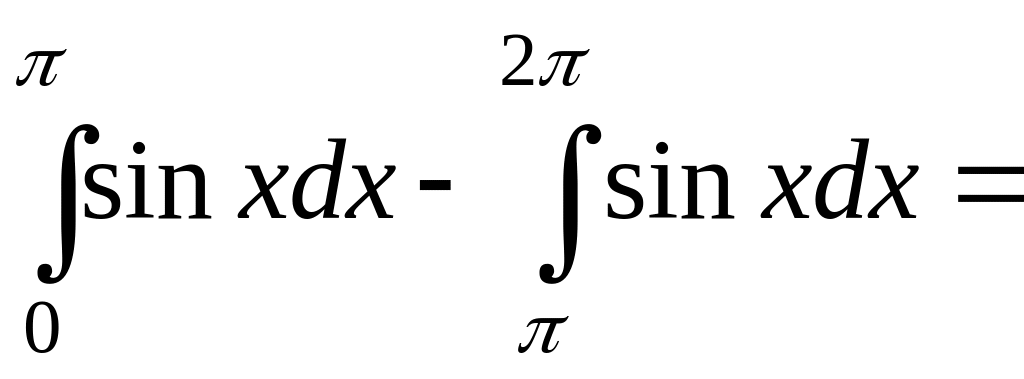

=-(-1-1)+(1-(-1))=2+2=4

14