
- •Интегральное исчисление функций одной переменной
- •§1. Первообразная функция и неопределенный интеграл
- •1. Понятие первообразной функции и неопределенного интеграла
- •2.Свойства неопределенного интеграла
- •§2. Основные методы интегрирования
- •1. Замена переменной интегрирования и подстановка
- •2. Интегрирование по частям
- •§3. Интегрирование дробно-рациональных функций
- •1. Основные понятия
- •2. Интегрирование простейших рациональных дробей
- •3. Разложение правильной рациональной дроби на простейшие
- •§4. Интегрирование тригонометрических выражений
- •§5. Интегрирование простейших иррациональностей
- •§6. Определённый интеграл
- •1. Понятие определённого интеграла
- •2.Формула Ньютона-Лейбница.
- •3. Свойства определенного интеграла.
- •§7. Вычисление площадей плоских фигур
2. Интегрирование по частям
Пусть u=u(x) и v=v(x) – непрерывно дифференцируемые функции, тогда d(u·v)=v·du+u·dv, udv=d(u·v)–v·du
Интегрируя левую и правую части данного равенства, получим
![]() (3)
(3)
Это и есть формула интегрирования по частям.
Примеры.
Вычислить
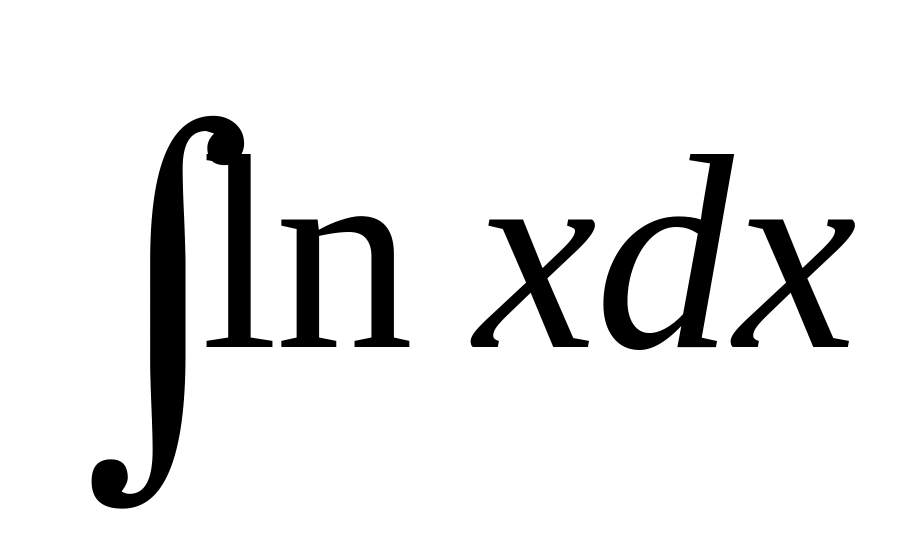 .
.
Положим u=lnx,
dv=dx.
Тогда du=d(lnx)=![]() ·dх
, v=x.
Следовательно,
·dх
, v=x.
Следовательно,
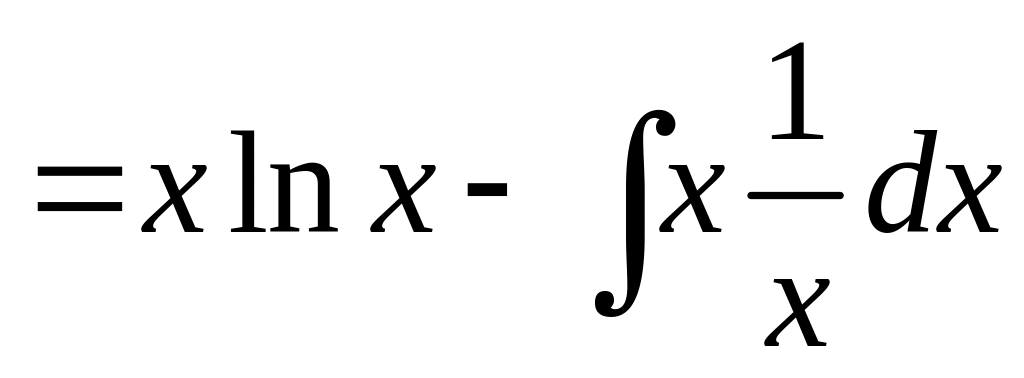
![]()
![]() .
.
Вычислить
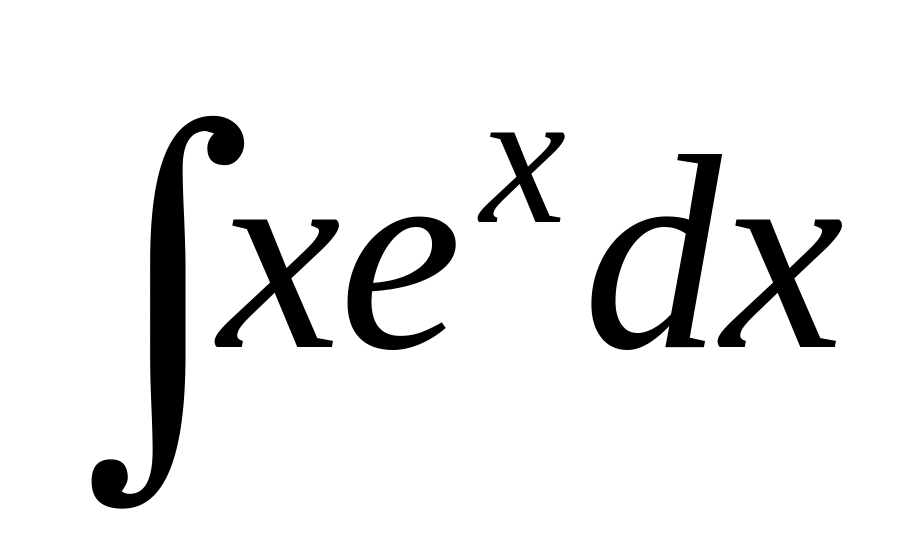 .
.
Положим u=x,
dv=exdx.
Положим du=dх,
![]() =
=![]() ,
v=еx.
Значит,
,
v=еx.
Значит,
![]()
§3. Интегрирование дробно-рациональных функций
1. Основные понятия
Определение. Дробно-рациональной функцией ( или рациональной дробью) называется отношение двух многочленов.
Рациональная дробь
называется правильной (неправильной),
если степень многочлена, стоящего в
числителе меньше (больше или равна)
степени многочлена, стоящего в знаменателе,
например, дроби:
![]() ;
;
![]() ;
;
![]() -
правильные, а дроби:
-
правильные, а дроби:
![]() ;
;
![]() - неправильные.
- неправильные.
Неправильную рациональную дробь всегда можно свести к правильной, разделив числитель на знаменатель столбиком и выделив из дроби целую часть, т.е. многочлен. Поэтому будем рассматривать задачу интегрирования правильной рациональной дроби, т.к. интегрирование многочлена не представляет труда. Всякую правильную рациональную дробь можно представить в виде суммы конечного числа так называемых простейших дробей следующих 4-х типов:
1.
![]() 2.
2.
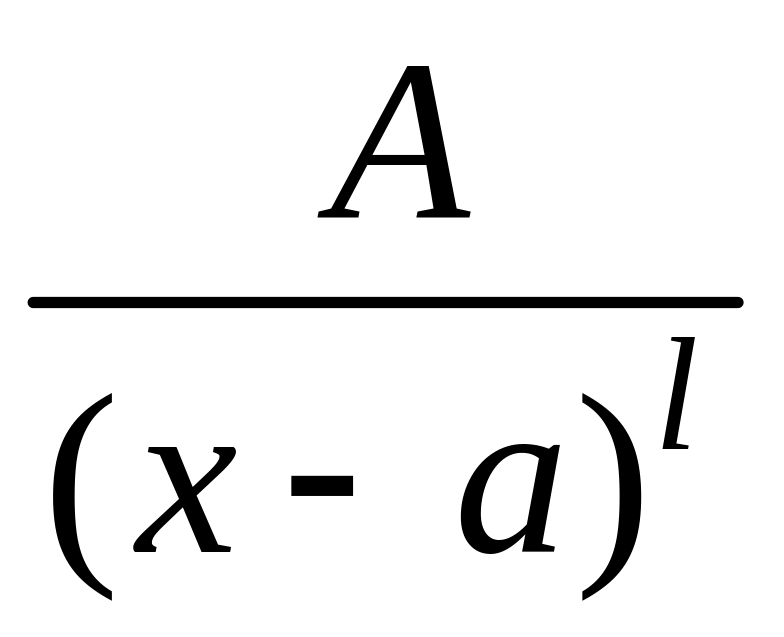 3.
3.
![]() 4.
4.
![]() ,
,
где A, M, N, a, p, q – действительные числа, ℓ = 2, 3…, квадратный трехчлен х2+рх+q –не имеет действительных корней.
2. Интегрирование простейших рациональных дробей
1.
![]() =
=![]() =А
=А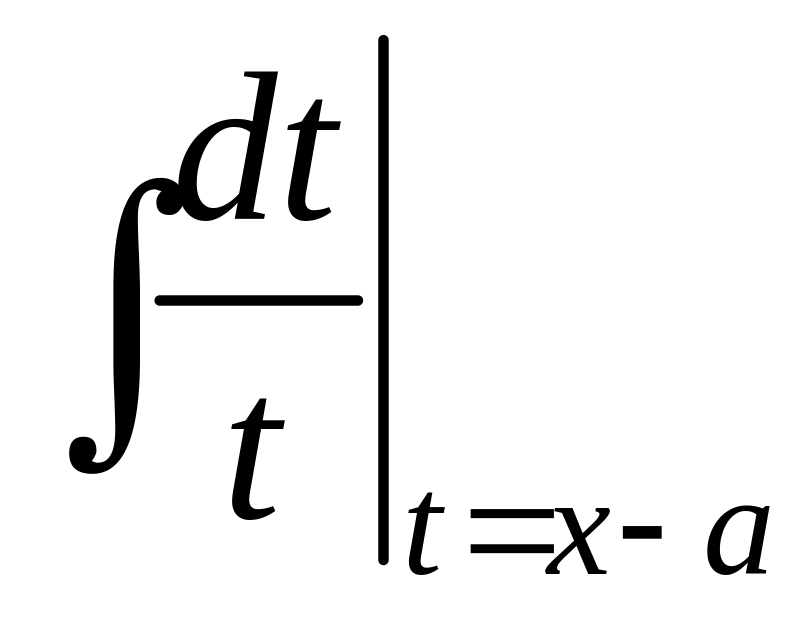 =Аln|t|+C=Aln|x-a|+C.
=Аln|t|+C=Aln|x-a|+C.
2.
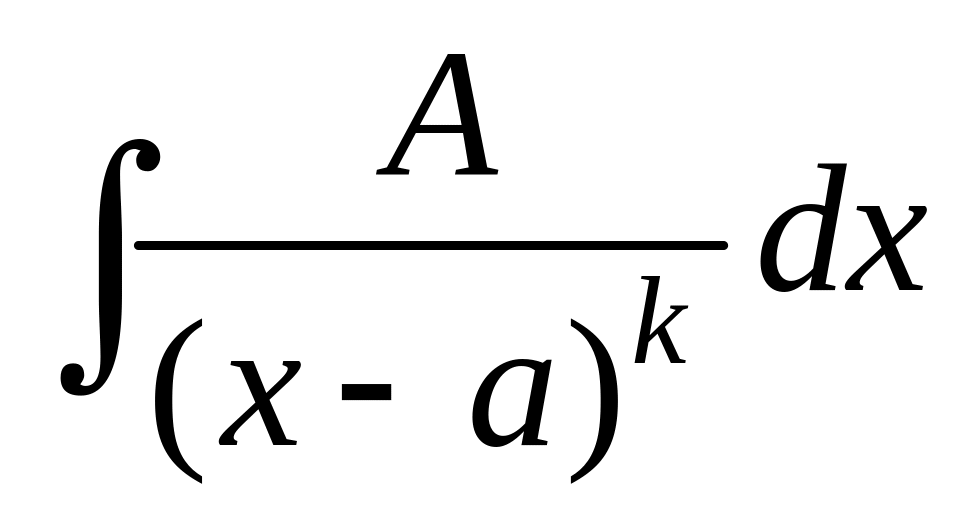 =A
=A![]() A
A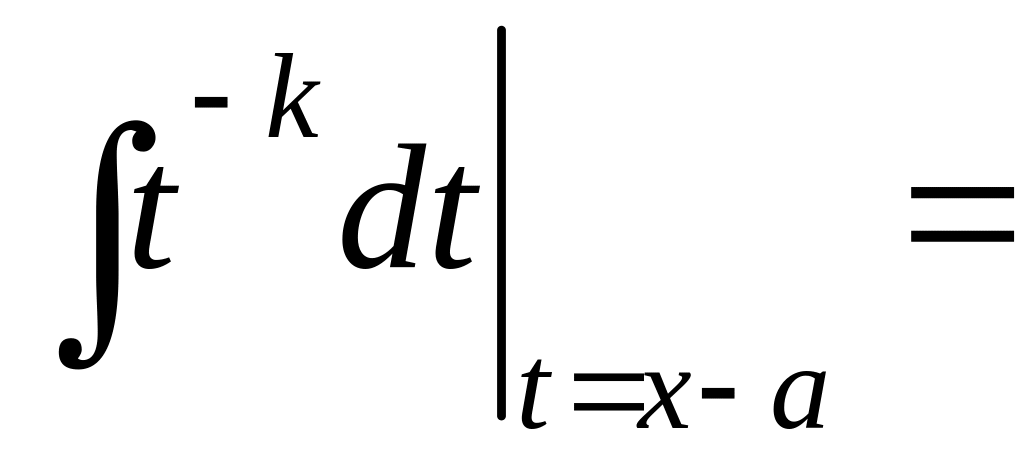 A
A![]() =
=
=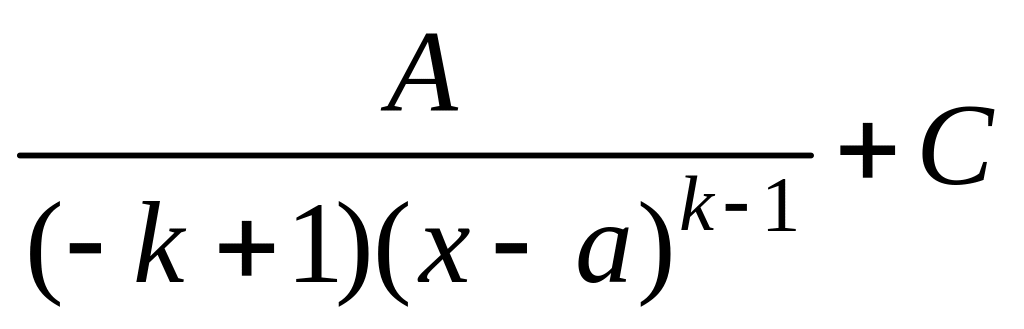 ,
(k-1).
,
(k-1).
3.
![]() =
=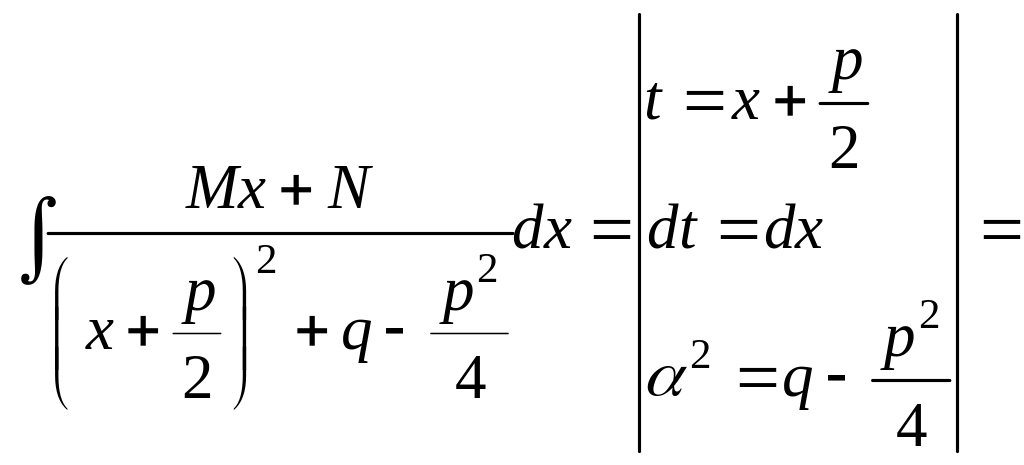
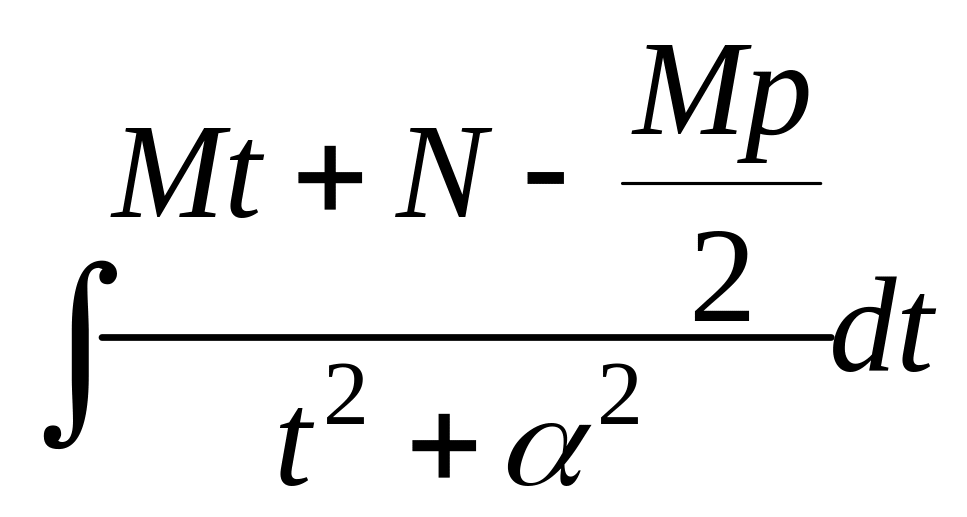 =
=
=![]() =
=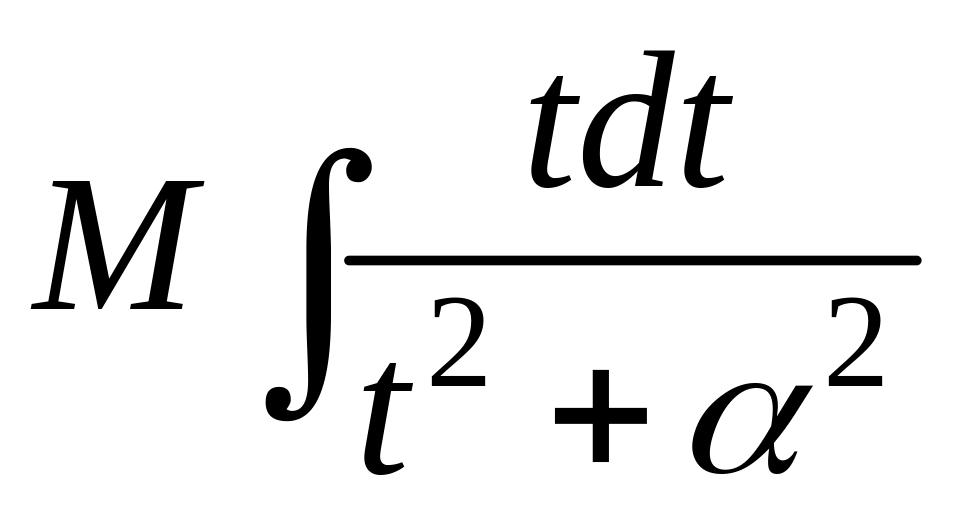 +
+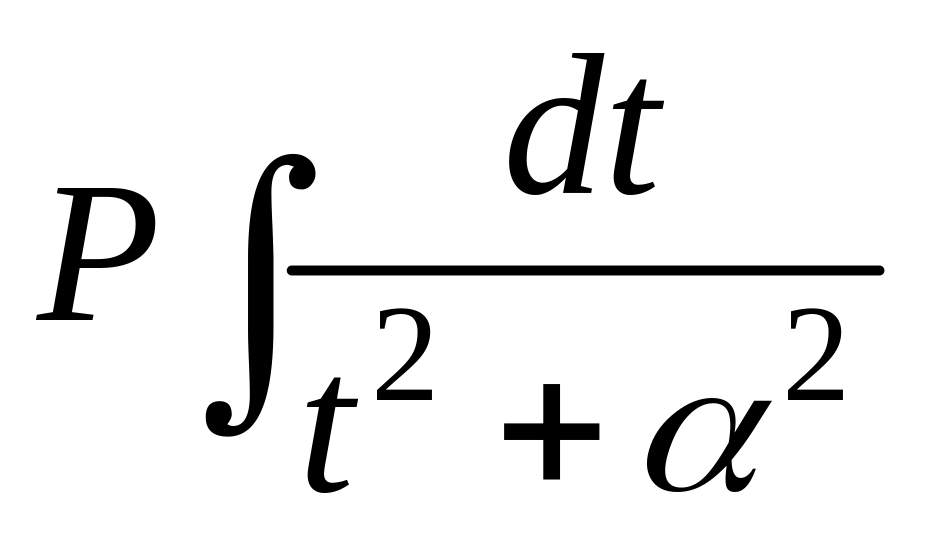 =
=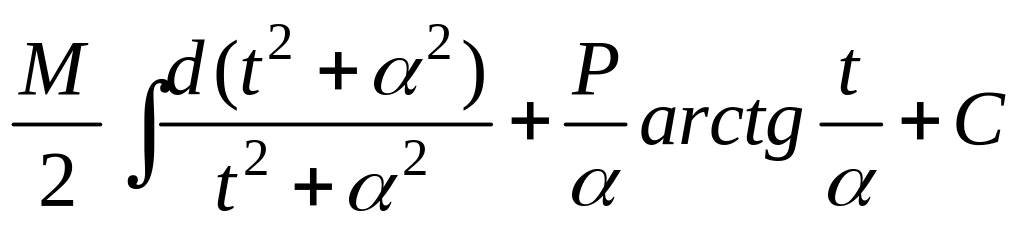 =
=
=![]() ln|t2+α2|+
ln|t2+α2|+![]() arctg
arctg![]() +C=
+C=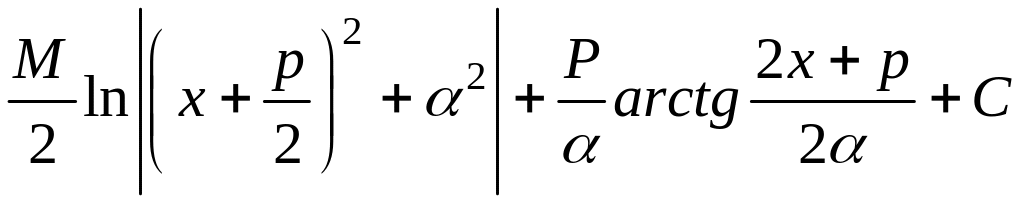 ,
,
где
![]() .
.
3. Разложение правильной рациональной дроби на простейшие
Пусть дана правильная
рациональная дробь: (1)
![]() .
Без ограничения общности можно считать,
что коэффициент у старшего члена
многочлена Q(х) равен 1, т.к. в случае,
когда он равен какому-то другому числу,
можно разделить числитель и знаменатель
дроби на это число. После чего у
получившегося в знаменателе многочлена
коэффициент у старшего члена окажется
равным 1. Будем предполагать, что
коэффициенты, входящие в дробь многочлена
– действительные числа. Для многочленов
с действительными коэффициентами имеет
место соответствующее разложение на
множители. Пусть для определенности
знаменатель Q(х) разлагается на множители
следующим образом: (2) Q(х)=(х-а)к·(х2
+рх+q)ℓ
, где
.
Без ограничения общности можно считать,
что коэффициент у старшего члена
многочлена Q(х) равен 1, т.к. в случае,
когда он равен какому-то другому числу,
можно разделить числитель и знаменатель
дроби на это число. После чего у
получившегося в знаменателе многочлена
коэффициент у старшего члена окажется
равным 1. Будем предполагать, что
коэффициенты, входящие в дробь многочлена
– действительные числа. Для многочленов
с действительными коэффициентами имеет
место соответствующее разложение на
множители. Пусть для определенности
знаменатель Q(х) разлагается на множители
следующим образом: (2) Q(х)=(х-а)к·(х2
+рх+q)ℓ
, где
![]() -q<0.
-q<0.
Теорема. Для дроби (1), знаменатель которой имеет вид (2), справедливо следующее разложение на сумму простейших дробей.
(3)
![]() =
=![]()
![]() +…+
+…+![]() +
+![]() …+
…+![]()
где А1, А2 ,… Ак, М1, N1,… Ml , Nl - постоянные действительные числа.
Из формулы (3) видно, что линейному множителю х-а знаменателя Q(х) соответствует в разложении (3) простейшие дроби типов (1), (2), а квадратному множителю: х2+рх+q – простейшие дроби типов (3) и (4). При этом число простейших дробей, соответствующих данному множителю (линейному или квадратичному) равно показателю степени, с которой этот множитель входит в разложение знаменателя дроби на множители.
Одним из наиболее простых методов нахождения коэффициентов при разложении правой рациональной дроби на простейшие является метод неопределенных коэффициентов.
Пример.
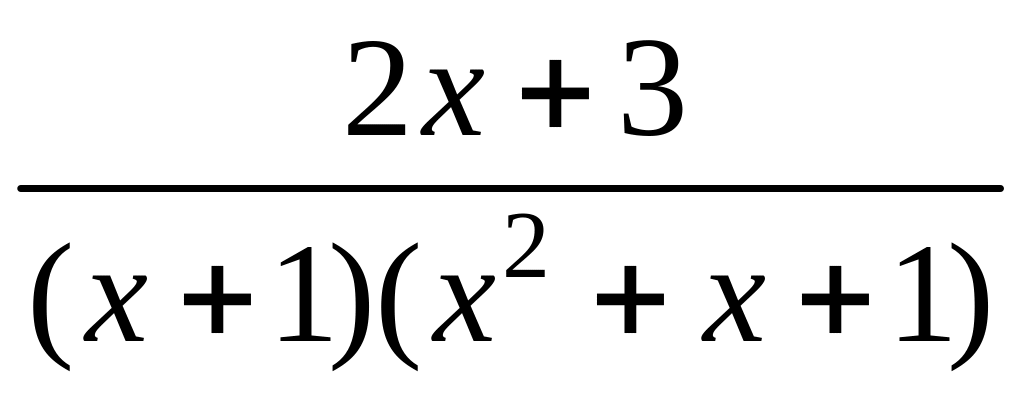 =
=![]()
![]() =
=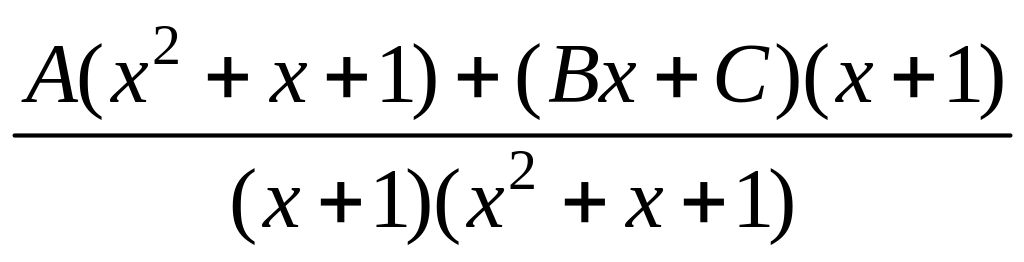 =
=
=![]() =
=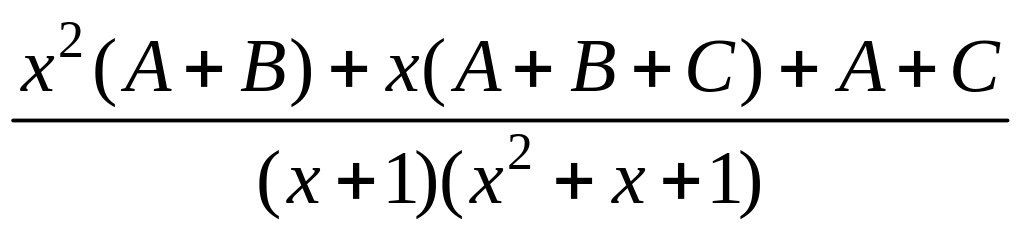
2х+3=х2·(А+В)+х·(А+В+С)+А+С
Из равенства двух многочленов следует равенство коэффициентов при одинаковых степенях х.
х2: А+В=0,
х: А+В+С=2,
хо : А+С=3.
Отсюда находим:
В=-А, С=3-А,
А–А+3–А=2, А=1, В=-1, С=2.
Тогда
![]() =
=![]() .
.
![]() =
=![]() +
+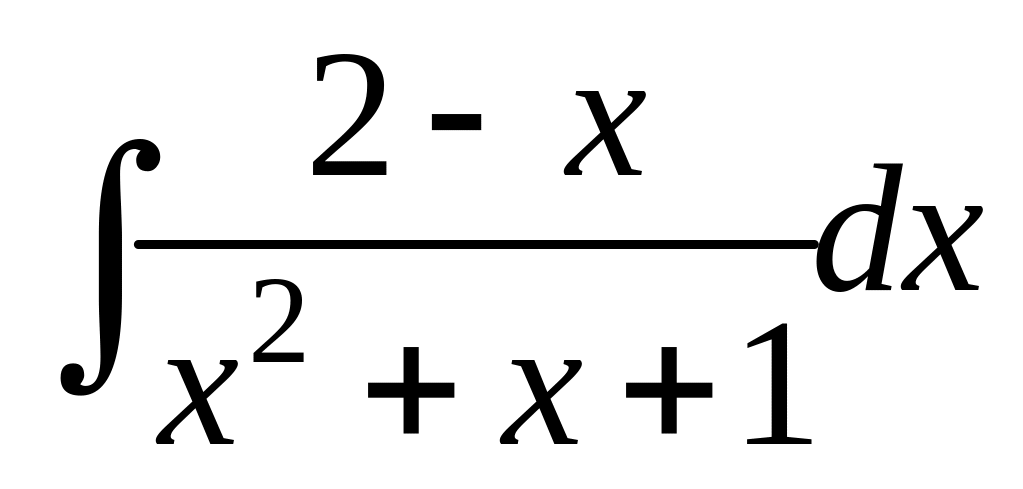
Вычислим второй интеграл. Преобразуем числитель таким образом, чтобы в нем находилась производная знаменателя и свободный член
(х2+х+1)=2х+1; (2х+1)dх=d(х2+х+1)
![]() =-
=-
![]() =
=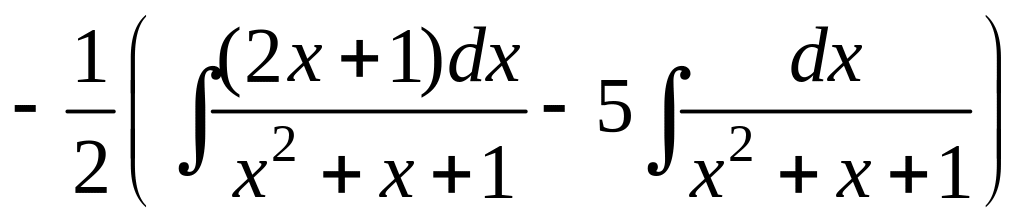 =
=
=-
![]()
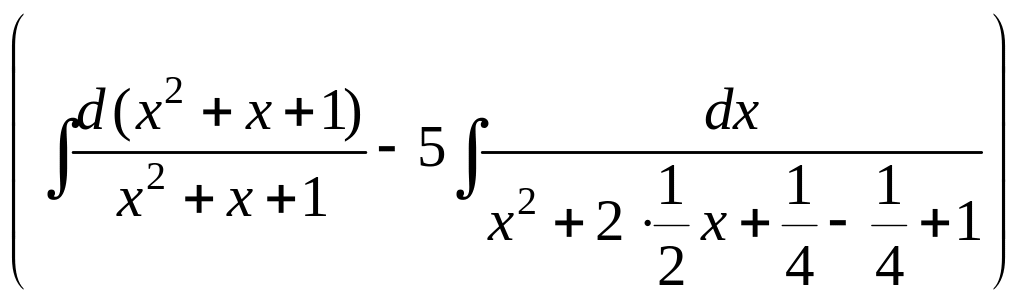 =
=
=-
ln|х2+х+1|+C+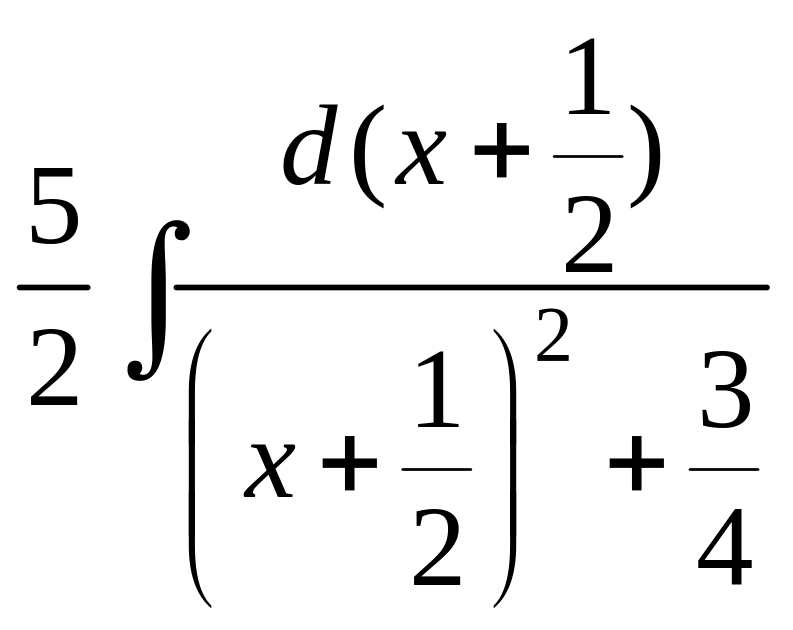 =-
ln(х2+х+1)+
=-
ln(х2+х+1)+![]() arctg
arctg![]()
Тогда =ln|x+1|- ln(х2+х+1)+ arctg +C=
=![]() +
arctg
+C.
+
arctg
+C.
