
- •Интегральное исчисление функций одной переменной
- •§1. Первообразная функция и неопределенный интеграл
- •1. Понятие первообразной функции и неопределенного интеграла
- •2.Свойства неопределенного интеграла
- •§2. Основные методы интегрирования
- •1. Замена переменной интегрирования и подстановка
- •2. Интегрирование по частям
- •§3. Интегрирование дробно-рациональных функций
- •1. Основные понятия
- •2. Интегрирование простейших рациональных дробей
- •3. Разложение правильной рациональной дроби на простейшие
- •§4. Интегрирование тригонометрических выражений
- •§5. Интегрирование простейших иррациональностей
- •§6. Определённый интеграл
- •1. Понятие определённого интеграла
- •2.Формула Ньютона-Лейбница.
- •3. Свойства определенного интеграла.
- •§7. Вычисление площадей плоских фигур
Интегральное исчисление функций одной переменной
§1. Первообразная функция и неопределенный интеграл
1. Понятие первообразной функции и неопределенного интеграла
Для дифференцирования существует обратное действие – интегрирование: отыскание функции по заданной её производной.
Определение 1. Функция F(х) называется первообразной функцией для функции f(x) на данном промежутке, если она дифференцируема на этом промежутке и F(х)=f(x).
Пример: Функция F(х) = х3 является первообразной функции f(x) =3х2 на всей числовой оси, т.к. при любом х (х3) =3х2 . Отметим при этом, что вместе с функцией F(х)=х3 первообразной для f(x)=3х2 является любая функция Ф(х)=х3+C, где С – произвольная константа.
Теорема 1. Если F1(х) и F2(х) - две первообразные функции для функции f(x) в некотором промежутке, то разность между ними в этом промежутке равна постоянному числу.
Доказательство.
Пусть, например, указанный промежуток – интервал (а; b). Из определения первообразной функции имеем: F1(х)= f(x) , F 2 (х) = f(x) для х из (а; b). Пусть α(x) = F2(х) - F1(х), тогда для любого х из (а; b)
α (x)=F 2 (х) - F1(х)=f(x) - f(x)=0 α(x)=С.
Подчеркнем важный факт: если производная для функции одна, т.е. операция дифференцирования однозначна, то нахождение первообразной для функции возможно лишь с точностью до некоего постоянного слагаемого.
Определение 2.
Выражение F(х)
+ С, где F(х)
– первообразная функции f(x)
и С – произвольная постоянная, называется
неопределенным
интегралом
от функции f
(x)
и обозначается символом
![]() ,
причем f(x)
называется подынтегральной функцией,
f(x)dх
– подынтегральным выражением, х –
переменной интегрирования, знак
,
причем f(x)
называется подынтегральной функцией,
f(x)dх
– подынтегральным выражением, х –
переменной интегрирования, знак
![]() - знаком интеграла. Таким образом, по
определению,
=
F(х)
+С, если F(х)
= f(x).
- знаком интеграла. Таким образом, по
определению,
=
F(х)
+С, если F(х)
= f(x).
Теорема 2. Если функция f(x) непрерывна на отрезке, то на этом отрезке у функции f(x) существует первообразная.
2.Свойства неопределенного интеграла
Из определения неопределенного интеграла непосредственно следует его свойства
1.
![]() =f(x)
=f(x)
Доказательство.
= F(х) +С. Продифференцируем левую и правую части равенства по переменной х.
![]() =(F(х)
+С)
;
=
F(х);
= f(x).
=(F(х)
+С)
;
=
F(х);
= f(x).
2.
![]() = F(х)
+С
= F(х)
+С
3.
![]() =
=
![]()
4.
![]() =
=
![]() +
+![]()
Основная таблица интегралов
1.
![]() =
=
![]() +С;
α
-1
+С;
α
-1
2.
![]() =
ln |x| +C
=
ln |x| +C
3.
![]() =
=
![]()
4.
![]() = ex
+C
,
= ex
+C
, ![]() =
=![]()
![]() +C
+C
5.
![]() ,
,
![]()
6.
![]() ,
,
![]()
7.
![]() = tg x + C ,
= tg x + C , 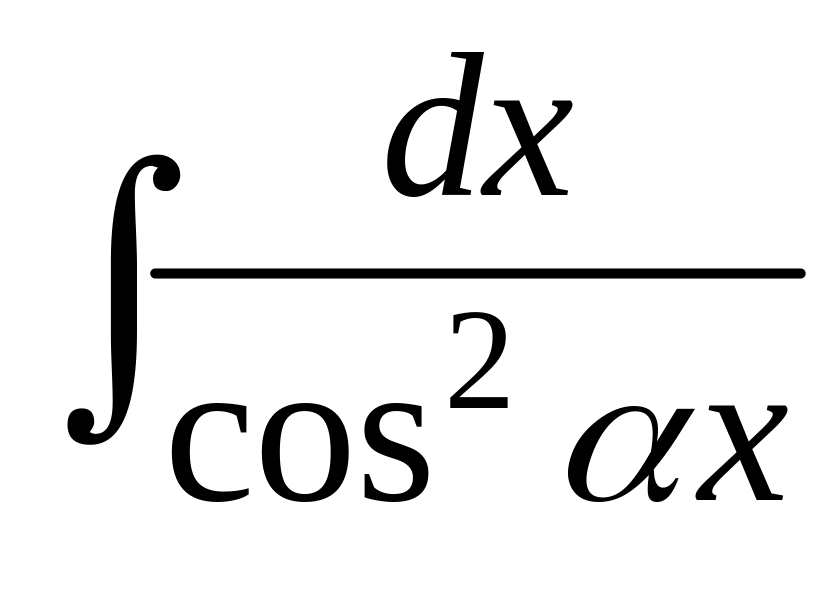 =
=
![]() tg αx
+ C
tg αx
+ C
8.
![]() =
- ctg x + C,
=
- ctg x + C, 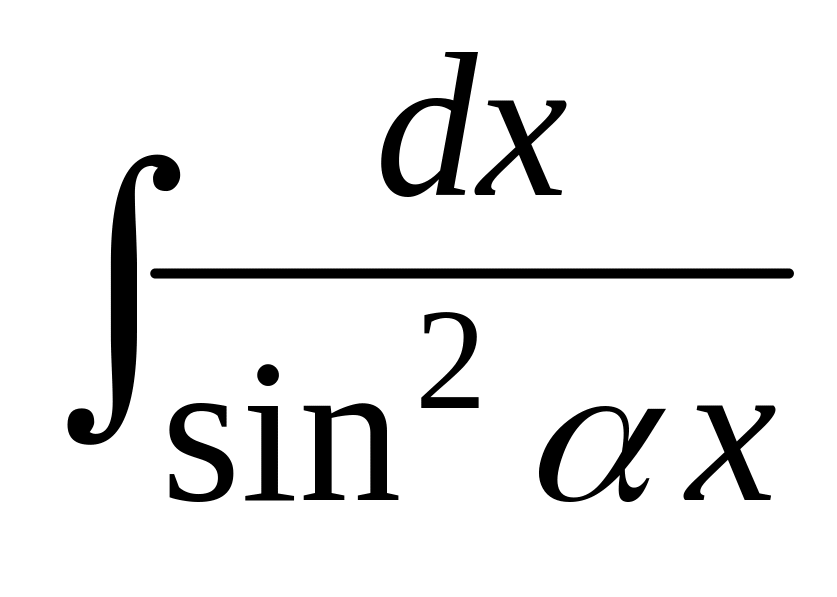 =
=
![]() ·
ctg αx
+ C
·
ctg αx
+ C
9.
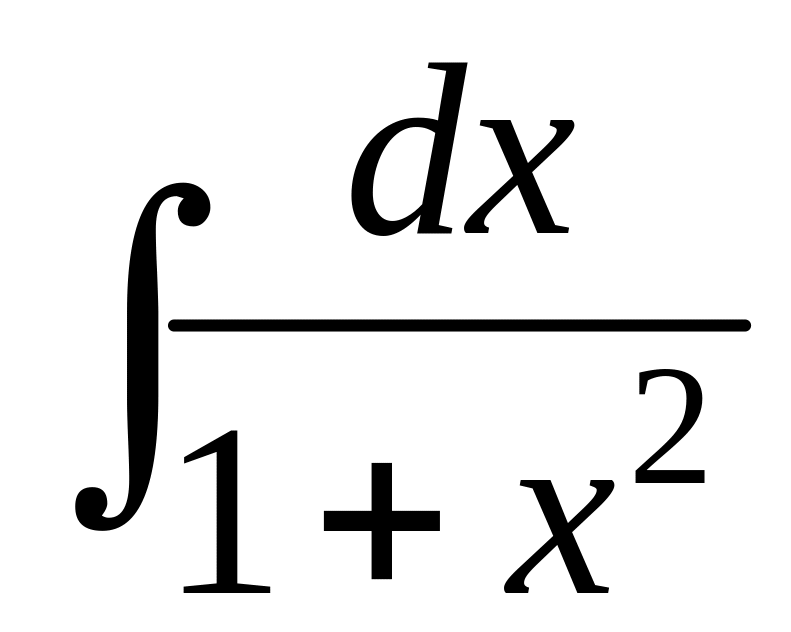 =
arctg x + C
=
arctg x + C
10.
![]() =
arcsin x + C
=
arcsin x + C
11.
![]() =
=![]() ln
ln![]() + C
+ C
12.
![]() =
ln
=
ln![]() +С
+С
13.
![]() =
=![]() arctg
arctg![]() +C
+C
14.
![]() =arcsin
+C
=arcsin
+C
15.
![]() =
=
![]() ln
ln![]() + C
+ C
§2. Основные методы интегрирования
1. Замена переменной интегрирования и подстановка
Этот способ часто бывает полезным в тех случаях, когда интеграл не может быть непосредственно преобразован к виду табличного. Сделаем подстановку: х =(t) , где (t) - функция, имеющая непрерывную производную. Тогда f(x)=f((t)), dх=d(t)=(t)·dt
=
![]() (1)
(1)
Формула (1) называется формулой подстановки в неопределенном интеграле.
Пример 1.
Вычислить
![]() .
.
Положим
![]() =t.
Тогда x
= t2
,
=t.
Тогда x
= t2
,
![]() =
=
![]() ,
,
![]() =dt2
=(t2)·dt=2t·dt.
=dt2
=(t2)·dt=2t·dt.
Получим
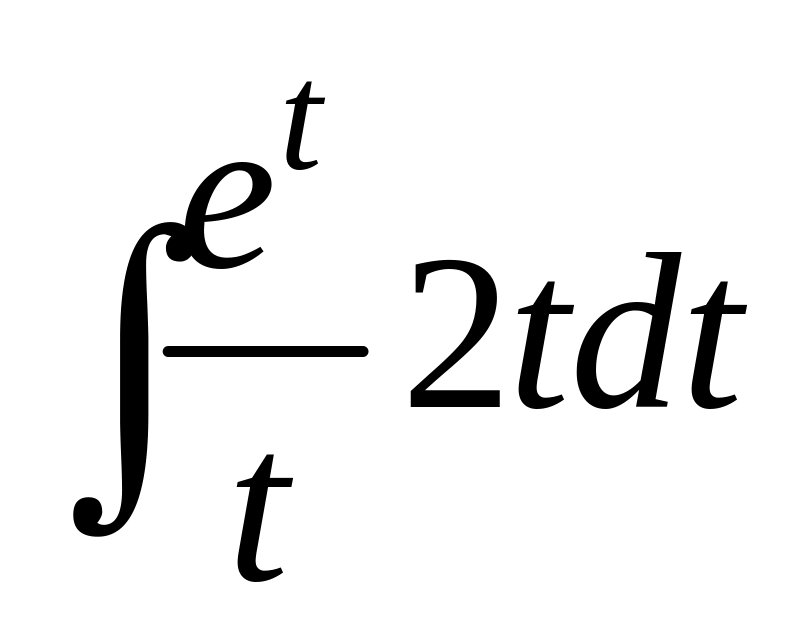
![]()
![]() .
.
Пример 2.
Вычислить
![]() .
.
Положим ех=t
, получаем е -х=![]() ,
lnex=ln
t,
x=ln
t,
dx=d(ln
t)=(ln
t)dt=
,
lnex=ln
t,
x=ln
t,
dx=d(ln
t)=(ln
t)dt=![]() и
и
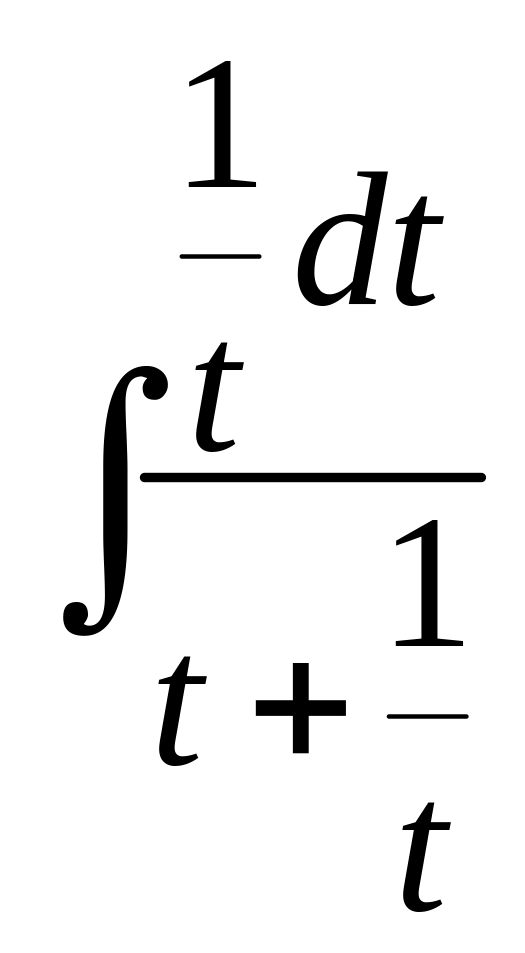 =
=
![]() =
arctg t + C = arctg ех
+ C
=
arctg t + C = arctg ех
+ C
Иногда вместо подстановки х=(t) лучше выбрать замену переменной вида (х)=t. Формула замены переменной имеет вид:
![]()
![]() , (2)
, (2)
где (х)dx=dt.
Применяя формулу замены переменной удобно пользоваться таблицей дифференциалов и следующим фактом:
![]() =
=![]()
Примеры.
1)
![]() =
=![]() =
=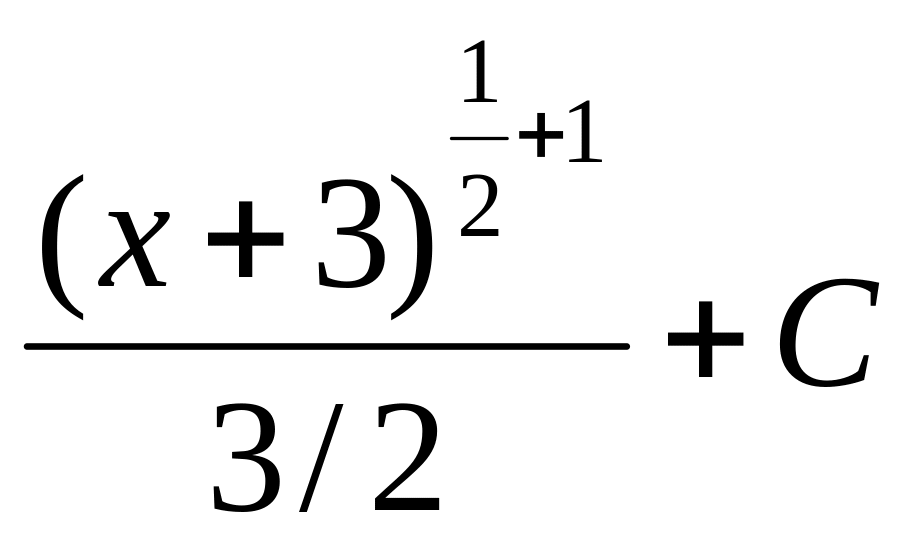 =
=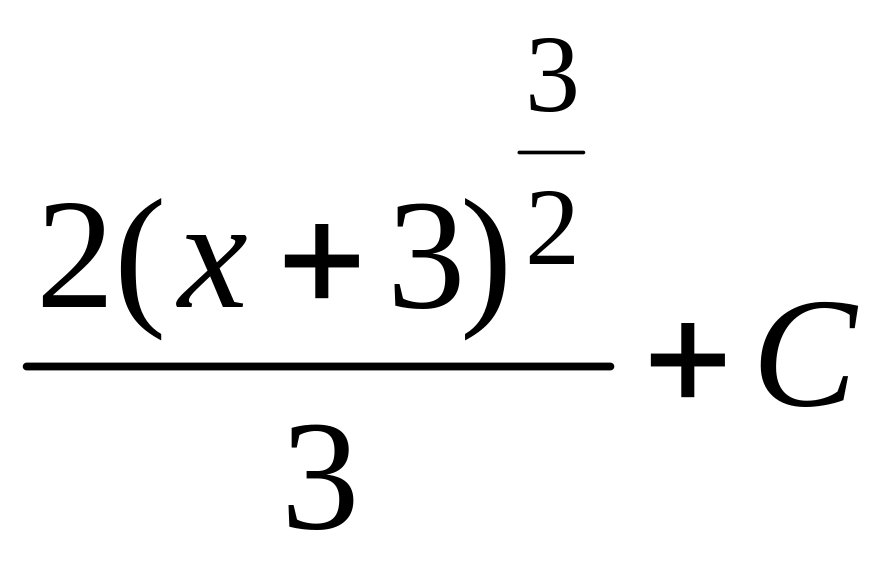
2)
![]() =
=![]()
![]() =
=![]()
3)
![]() =
=![]() =
=
![]()
