Вариант 5
Вычислить неопределённый интеграл:
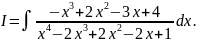
Решить кубическое уравнение
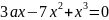относительно
.Построить график функции , задать оптимальные границы области построения.
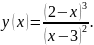
Задать с помощью матрицы размером 8×8 растровое изображение. Значение элемента 0 соответствует чёрному цвету, 255 — белому. Промежуточные значения будут представлены оттенками серого. Изображение увеличить.
Создать две матрицы A и B размером 3×3. Одну из них транспонировать, а другую умножить на единичную матрицу 3×3. Полученные матрицы сложить и вычислить определитель результирующей матрицы.
Решить систему линейных уравнений методом Крамера:
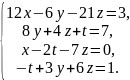
Выполнить проверку результата путём подстановки корней в одно из уравнений.
Решить систему уравнений из задания 6 при помощи символьных преобразований для корней x, y, z, t. Каждое уравнение системы записывается как один элемент вектора (одномерной матрицы).
Даны две матрицы:
,
.
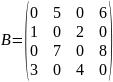С помощью индексных переменных i
и j
создать матрицу C,
элементы которой будут соответствовать
выделенным элементам матрицы A,
и матрицу D,
состоящую из выделенных элементов
матрицы B.
Полученные матрицы сложить. Последний
столбец полученной матрицы поместить
в переменную E,
используя функцию Matrix
Column.Построить трёхмерный график функции:
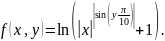
Создать анимацию, показывающую изменение графика функции:
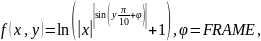
в зависимости от значения фазы . Переменная FRAME (счётчик кадров) является встроенной переменной MathCad, её значение увеличивается на 1 для каждого следующего кадра анимации. С помощью меню «Tools → Animation → Record…» задать номер первого («From») и последнего («To») кадра, а также частоту смены кадров «At: … Frames/Sec» (не менее 24 кадров/с). Выделить в рамку область с графиком, нажать на кнопку «Animate». Подобрать такие параметры анимации и выражение для , чтобы за 5 секунд анимации функция изменялась на полный период (значение фазы на последнем кадре достигало ).
Вариант 6
Вычислить неопределённый интеграл:
Решить уравнение:
Построить график функции , задать оптимальные границы области построения.
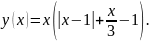
Задать с помощью матрицы размером 8×8 растровое изображение. Значение элемента 0 соответствует чёрному цвету, 255 — белому. Промежуточные значения будут представлены оттенками серого. Изображение увеличить.
Создать две матрицы A и B размером 3×3. Одну из них транспонировать, а другую умножить на единичную матрицу 3×3. Полученные матрицы сложить и вычислить определитель результирующей матрицы.
Решить систему линейных уравнений методом Крамера:
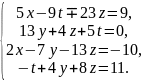
Выполнить проверку результата путём подстановки корней в одно из уравнений.
Решить систему уравнений из задания 6 при помощи символьных преобразований для корней x, y, z, t. Каждое уравнение системы записывается как один элемент вектора (одномерной матрицы).
Даны две матрицы:
,
.
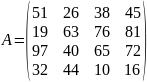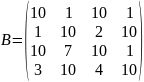С помощью индексных переменных i
и j
создать матрицу C,
элементы которой будут соответствовать
выделенным элементам матрицы A,
и матрицу D,
состоящую из выделенных элементов
матрицы B.
Полученные матрицы сложить. Последний
столбец полученной матрицы поместить
в переменную E,
используя функцию Matrix
Column.Построить трёхмерный график функции:
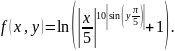
Создать анимацию, показывающую изменение графика функции:
в зависимости от значения фазы . Переменная FRAME (счётчик кадров) является встроенной переменной MathCad, её значение увеличивается на 1 для каждого следующего кадра анимации. С помощью меню «Tools → Animation → Record…» задать номер первого («From») и последнего («To») кадра, а также частоту смены кадров «At: … Frames/Sec» (не менее 24 кадров/с). Выделить в рамку область с графиком, нажать на кнопку «Animate». Подобрать такие параметры анимации и выражение для , чтобы за 5 секунд анимации функция изменялась на полный период (значение фазы на последнем кадре достигало ).