2.6. Расчет реактивной силы (тяги) (*)

Полет реактивного аппарата осуществляется под действием реактивной силы, или, как ее часто называют, тяги, которую сообщает ему струя выходящих газов. Для нахождения величины реактивной силы Р нет необходимости рассматривать де­тально распределение давления по внутренним и наружным стенкам реактивного аппарата. Реактивную силу можно опре­делить в конечном виде с помощью уравнения количества дви­жения.

Совершая полет, тело производит возмущение в окружаю­щей среде. Всегда можно выделить некоторую, достаточно боль­шую, например цилиндрическую, область, границы которой вы­ходят за пределы возмущенной части потока (рис. 2.3).

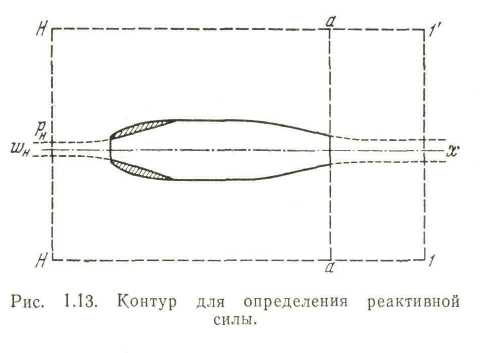
Рисунок 2.2. Контур для определения реактивной силы

На боковых границах этой области давление и скорость потока (считаем двигатель неподвижным, а воздух — движущимся со скоростью полета) равны их значениям на бесконечности перед двигателем.

Пусть ось х совпадает с направлением полета и является осью симметрии двигателя; спроектируем на ось х силы, дей­ствующие на двигатель и на поверхность выделенного контура. Так как силы давления в жидкости нормальны к поверхности, то проекции на ось х сил, действующих на боковые поверхности контура, обращаются в нуль. Поэтому уравнение Эйлера (см. (2.55)) запишется так:

Здесь площади, на которые распространяются интегралы, и область интегрирования первого члена правой части бесконечны Сила Р берется со знаком «+» потому, что при выводе формулы (2.55) предполагалось, что машина получает от газа работу, а здесь реактивный двигатель сообщает работу газу, G_B — се­кундная масса воздуха, втекающая в контур через сечение F; G_T — дополнительная секундная масса горючего, которая по­дается в двигатель

Если взять левую торцовую поверхность далеко перед дви­гателем, то давление на ней постоянно и равно атмосферному (р_н), а скорость потока равна скорости полета (w_н) Кроме того, можно допустить, что в поперечном направлении уже на неко­тором конечном расстоянии от поверхности двигателя поток яв­ляется невозмущенным и площадь F, на которую распростра­няются интегралы левой части, считать конечной, точно так же конечной будет и область интегрирования в первом члене пра­вой части. Тогда следует написать

В большом числе случаев возмущение, вызываемое летящим те­лом, настолько незначительно, что в плоскости среза сопла а (вне струи выхлопных газов) давление обтекающего потока мало отличается от давления на бесконечности (р_н). Тогда силы дав­ления на передней и задней торцовых поверхностях контура уравновешиваются везде, кроме участка, соответствующего по­перечному сечению выхлопной струи (F_a). Скорости потока во всех элементарных струйках, кроме проходящих через двига­тель, одинаковы (здесь мы пренебрегаем влиянием трения, вих­ревых и волновых потерь на наружной поверхности двигателя) Следовательно, изменение количества движения получается только в струе, протекающей сквозь двигатель. Тогда уравнение Эйлера принимает следующий вид

откуда получается основная формула для реактивной силы

(2.64)

В этих выражениях w_a — средняя скорость истечения

Следует подчеркнуть, что полученное соотношение справед­ливо только в том случае, если скорость и давление в плоско­сти а (за исключением участка рабочей струи) равны в точно­сти их значениям на бесконечности перед двигателем Кроме того, мы здесь пренебрегаем внешним лобовым сопротивлением двигателя, которое всегда может быть учтено отдельно.

На расчетном режиме работы реактивного двигателя давле­ние в выхлопной струе равно давлению окружающего воздуха (р_а = р_н), в этом случае тяга равна изменению количества движения газа, прошедшего через двигатель

(2.65)

В воздушно реактивных двигателях второй член правой части мал, и им часто пренебрегают (G_T=0,05…0,15G_В), т е принимают для воздушно-реактивных двигателей в расчетном случае

(2.66)

Тяга жидкостного реактивного двигателя, в котором не ис­пользуется атмосферный воздух, определяется для расчетного режима по формуле:

(2.67)

или на нерасчетном режиме

(2.68)

Здесь G_o — секундный массовый расход окислителя.