Алгоритм сочетания

В тех случаях, когда нас не интересует порядок элементов в комбинации, а интересует лишь ее состав, говорят о сочетаниях. Итак, k -сочетаниями из n элементов называют всевозможные k - расстановки, составленные из этих элементов и отличающиеся друг от друга составом, но не порядком элементов. Число k-сочетаний, которое можно составить из n элементов, обозначают через  .

Формула для числа сочетаний получается из формулы для числа размещений. В самом деле, составим сначала все k -сочетания из n элементов, а потом переставим входящие в каждое сочетание элементы всеми возможными способами. При этом получается, что все k -размещения из n  элементов, причем каждое только по одному разу. Но из каждого k - сочетания можно сделать 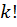  перестановок, а число этих сочетаний равно  . Значит, справедлива формула:

Из этой формулы находим, что

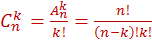
Например, имеем 5 компонент, обозначенных латинскими буквами A, B, C, D, E. Тогда все сочетания из этих 5 компонент по 3, выписанные в лексикографическом порядке, будут таковы:

• для букв – ABC, ABD, ABE, ACD, ACE, ADE, BCD, BCE, BDE, CDE;

• для цифр – 123, 124, 125, 134, 135, 145, 234, 235, 245, 345.

Контрольные вопросы

1. Дать определение комбинаторным вычислениям.

2. Дать понятие класса алгоритма. Какие свойства заложены в классе алгоритма решения задачи о фальшивой монете.

3. Как осуществляется анализ алгоритмов?

4. Принцип алгоритма размещения без повторений. Математическая формула алгоритма.

5. Принцип алгоритма перестановки. Математическая формула алгоритма.

6. Принцип алгоритма сочетаний. Математическая формула алгоритма.