
- •1)Дать определение линейной зависимости векторов
- •2)Дать определение линейно независимой системы векторов
- •3)Дать определения базиса линейного пространства
- •9)Дать определение евклидова пространства
- •18) Сформулировать свойство инвариантности характеристического уравнения линейного оператора
- •29)Сформулировтаь теорему о существовании для самосопряженного оператора ортонормированного базиса,в котором его матрица имеет простой вид
- •30)Сформулировать теорему о собственных векторах самосопряженного оператора,соответствующих различным собственным значениям
- •31)Описать алгоритм приведения матрицы самосопряженного оператора к диагональному виду
- •32)Сформулировать утверждение о матрице перехода от одного ортонормированного базиса к другому
- •33)Дать определение ортогональной матрицы
- •34)Сформулировать свойства ортогональной матрицы
29)Сформулировтаь теорему о существовании для самосопряженного оператора ортонормированного базиса,в котором его матрица имеет простой вид
Для любого самосопряженного оператора A существует ортонормированный базис, состоящий из собственных векторов оператора A. Матрица A линейного оператора A в этом базисе имеет диагональный вид, на диагонали расположены собственные значения оператора A, повторяющиеся столько раз, какова их кратность.
30)Сформулировать теорему о собственных векторах самосопряженного оператора,соответствующих различным собственным значениям
Собственные векторы самосопряженного оператора, отвечающие различным собственным значениям, ортогональны.
31)Описать алгоритм приведения матрицы самосопряженного оператора к диагональному виду
Теорема. Матрица самосопряженного оператора в собственном базисе имеет диагональную форму. Ясно, что для того чтобы привести матрицу самосопряженного оператор к диагональному виду нужно найти собственные значения оператора и диагональную матрицу, на диагонали которой расположены собственные значения матрицы. Если нужно записать выражение для приведения матрицы к этой диагональной форме, то нужно еще найти собственные векторы матрицы, записать матрицу C перехода к собственному базису (матрицу, столбцами которой являются координаты собственных векторов оператора), найти обратную к ней матрицу С-1 и тогда — равенство, связывающее диагональну форму матрицы оператора в собственном базисе с матрицей A оператора в заданном базисе.
записываем матрицу оператора
 в
исходном базисе;
в
исходном базисе;записываем характеристическое уравнение и вычисляем его корни;
находим собственный базис оператора (если он существует);
записываем матрицу
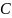 , столбцами
которой являются координаты собственных
векторов (векторов собственного базиса);
, столбцами
которой являются координаты собственных
векторов (векторов собственного базиса);по формуле
 находим
диагональную форму матриц оператора
— матрицу оператора в собственном
базисе.
находим
диагональную форму матриц оператора
— матрицу оператора в собственном
базисе.
32)Сформулировать утверждение о матрице перехода от одного ортонормированного базиса к другому
Матрица перехода от одного ортонормированного базиса к другому ортонормированному базису — ортогональная.
Матрицей
перехода
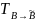 от базиса
от базиса
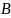 к базису
к базису
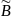 называется матрица
называется матрица
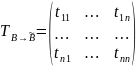 ,
,
 столбец которой есть столбец
столбец которой есть столбец
 координат вектора
координат вектора
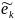 в базисе
.
Если
в базисе
.
Если
 – произвольный вектор из
– произвольный вектор из
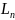 ,
,
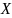 и
и
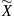 – столбцы его координат в базисах
и
соответственно, то имеет место равенство
– столбцы его координат в базисах
и
соответственно, то имеет место равенство
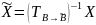 (формула преобразования координат при
преобразовании базиса).
(формула преобразования координат при
преобразовании базиса).
33)Дать определение ортогональной матрицы
Квадратную
матрицу
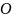 называют ортогональной, если она
удовлетворяет условию
называют ортогональной, если она
удовлетворяет условию
 ,
где
,
где
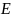 – единичная матрица.
– единичная матрица.
34)Сформулировать свойства ортогональной матрицы
1.
Определитель ортогональной матрицы
может иметь одно из двух возможных
значений:
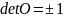
2.
Матрица, обратная к ортогональной
матрице
,
совпадает с ее транспонированной
матрицей, т.е.
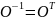 .
.
3.
Произведение ортогональной матрицы
на транспонированную к ней равно
единичной матрице, т.е.
 .
.
4. Матрица, транспонированная к ортогональной матрице, тоже является ортогональной.
5.
Произведение двух ортогональных матриц
и
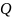 одного порядка является ортогональной
матрицей.
одного порядка является ортогональной
матрицей.
6. Матрица, обратная к ортогональной матрице, тоже является ортогональной.
— ортогональная.
Матрицей перехода от базиса к базису называется матрица , столбец которой есть столбец координат вектора в базисе . Если – произвольный вектор из , и – столбцы его координат в базисах и соответственно, то имеет место равенство (формула преобразования координат при преобразовании базиса).
