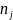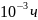Задание №1

Как относятся понятия «качество» и «надежность» автомобиля?

Качество — совокупность свойств продукции, определяющих ее пригодность для использования по назначению. Эти свойства изделия обычно проявляются в процессе его эксплуатации, т.е. способности сохранять установленные показатели в течение возможно более длительного времени.

Основными свойствами, определяющими качество изделий (автомобиля), являются следующие свойства:

• эксплуатационные и потребительские свойства;

• надежность и долговечность;

• технологичность;

• эстетические и эргономические показатели;

• степень стандартизации и унификации узлов автомобиля.

Вследствие этого потребительским спросом на рынке пользуются автомобили с высокими эксплуатационными показателями паспортных данных, такими как мощность, скорость, расход топлива и т.д. Кроме того, на спрос оказывает влияние свойство технологичности при техническом обслуживании и ремонте автомобиля. Проявляется свойство в том, что быстро изнашиваемые и часто заменяемые стандартные узлы и детали располагаются в автомобиле в местах, легкодоступных для их замены с использованием стандартных приспособлений и инструмента, например, замена масляного фильтра, воздушного фильтра, свеч и т.д.

Наиболее важным свойством качества является надежность. Под надежностью понимают способность машины сохранять свои эксплуатационные свойства в течение определенного времени и в определенных условиях. При изменении условий эксплуатации меняется и надежность автомобиля, так, автомобили иностранных марок не всегда показывают такую же надежность на дорогах России по сравнению с зарубежными данными.

Необходимо отметить, что надежность тесно связана с трудозатратами на техническое обслуживание и ремонт. Обычно стоимость запасных частей значительно превышает стоимость самих машин.

Характеризуется надежность рядом признаков, свойств, основными из них являются работоспособность, безотказность, долговечность, ремонтопригодность.

Безотказность (ГОСТ 27.002-89) - свойства объекта непрерывно сохранять работоспособное состояние в течение некоторого времени или наработки.

Долговечность (ГОСТ 27.002-89) - свойство объекта сохранять работоспособное состояние до наступления предельного состояния при установленной системе технического обслуживания и ремонта.

Ремонтопригодность (ГОСТ 27.002-89) - свойство объекта, заключающееся в приспособленности к поддержанию и восстановлению работоспособного состояния путем технического обслуживания и ремонта.

Сохраняемость (ГОСТ 27.002-89) - свойство объекта сохранять в заданных пределах значения параметров, характеризующих способность объекта выполнять требуемые функции, в течение и после хранения и/или транспортирования.

Все вышеперечисленные показатели надежности являются единичными, т.е. характеризующими только одно какое-либо свойство надежности. Кроме них для оценки надежности используются и комплексные показатели, чаще всего оценивающие совместно свойства безотказности и (или) долговечности и ремонтопригодности. Например, коэффициент готовности Кг - вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течение которых применение объекта по назначению не производится.

Подытожив можно сделать вывод, что качество и надежность автомобиля тесно связаны между собой. Качественно сделанный автомобиль будет дольше находится в исправном состоянии, а следовательно он будет более надежен нежели другие менее качественные автомобили.

Задание №2

Расчетное определение количественных характеристик надежности по статистическим данным об отказах технического объекта.

Условие задания 2.1. В таблице 2 приведены значения наработок до отказа в находившейся под контролем партии топливных форсунок дизелей автомобилей. Требуется определить статистические вероятности безотказной работы 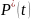и отказа 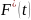форсунки для заданного значения времени t, указанного в таблице 2.

Затем для заданной наработки t требуется рассчитать математическое ожидание числа работоспособных устройств 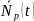при общем объеме партии находившихся в эксплуатации форсунок 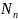указанном в таблице 3.

Таблица 2. Значения наработки устройства до отказа и заданные значения времени t

Таблица 3. Объем партии форсунок

Решение

Число форсунок, работоспособных к этому времени .

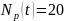Статистически вероятность безотказной работы форсунки для наработки :

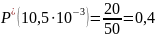
Статистически вероятность отказа форсунки за наработку

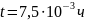
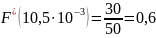
Выполним проверку:

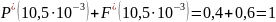
Математическое ожидание числа форсунок 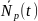, работоспособных к наработке :

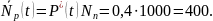
Условие задания 2.2. Требуется рассчитать среднюю наработку до отказа 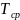рассматриваемых форсунок. Первоначально вычисления произвести непосредственно по выборочным значениям T, указанным в таблице 2, а затем с использованием статистического ряда. Оценить ошибку вычислений при использовании статистического ряда.

Решение

Для вычисления среднего значения T_ср случайной величины T непосредственно по ее выборочным значениям 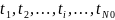используем формулу:

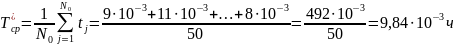
Выполним преобразование значений наработки до отказа в статистический ряд. Для этого заполним таблицу 4.

Таблица 4. Преобразование значений наработки до отказа в статистический ряд.

Интервал			Число попаданий на интервал				Статистическая вероятность
№ пп	Нижняя и верхняя границы,
1	4,5 – 7,5	///// /////		10		0,2
2	7,5 – 10,5	///// ///// ///// /////		20		0,4
3	10,5 – 13,5	///// ///// /////		15		0,3
4	13,5 – 16,5	/////		5		0,1

Проверим правильность расчётов:

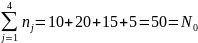
Изобразим статистический ряд графически на рис.1.

Рис. 1. Статистический ряд наблюдений

Статистическая вероятность 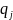попаданий случайной величины на j – й интервал рассчитывается как

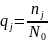
Выполним проверку:

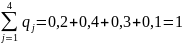
Для расчета среднего значения случайной величины в качестве «представителя» всех ее значений, принадлежащих j – му интервалу, принимают его середину 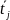. Тогда средняя наработка форсунок до отказа определяется по формуле:

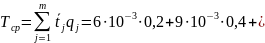
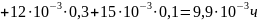
Расчет с использованием данной формулы вносит некоторую методическую ошибку. Эту ошибку оценим по формуле:

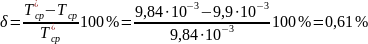
Условие задания 2.3. Требуется рассчитать интенсивность отказов форсунок 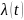для всех четырех интервалов и .

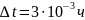Решение

Вычислим значение интенсивности отказов 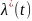, воспользовавшись выражением:

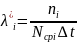
Следовательно, имеем:

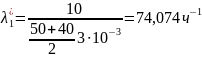
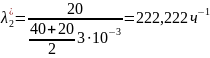
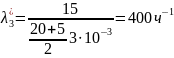
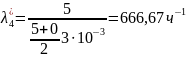
Задание №3

Аналитическое определение количественных характеристик надёжности технического изделия при известном законе распределения случайной величины.

Условие задания 3.1. Исследовать изменения функции надежности в интервале времени от 0 до t часов если время безотказной работы элемента автомобиля подчинено экспоненциальному закону распределения с заданными параметрами.

Таблица 5. Исходные данные. Экспоненциальный закон распределения.

Решение

Разобьём время на пять интервалов по 100 ч. Значение времени, соответствующие границам интервалов заносим в верхнюю строку таблицы 6. Во вторую строку таблицы – соответствующие им значения вероятности безотказной работы машины 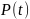, рассчитанные по формуле

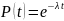
Таблица 6. Результаты расчётов функции надежности при экспоненциальном законе распределения

t, ч	0	100	200	300	400	500
P(t)	1	0,368	0,135	0,05	0,018	0,007

По полученным значениям строим график изменения функции надежности.

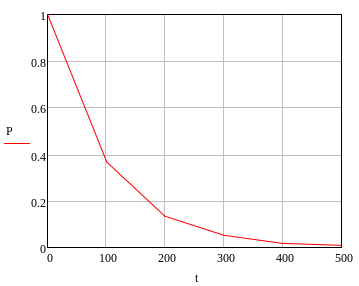
Рис. 2. Функция надежности при экспоненциальном законе распределения

Анализ зависимости функции надежности от времени показывает, что первые 80 часов вероятность безотказной работы уменьшается в два раза, а затем асимптотически приближается к нулю. После 250 часов вероятность безотказной работы составляет менее 10 %.

Условие задания 3.2. Исследовать изменения функции надежности в интервале времени от 0 до t часов если время безотказной работы элемента автомобиля подчинено нормальному закону распределения с заданными параметрами.

Таблица 7. Исходные данные. Нормальный закон распределения.