
- •Регресійний аналіз
- •Синтаксис
- •Примітки
- •41. Функція ковар.
- •Общие замечания
- •Функция стандотклон
- •Функции суммесли и счётесли [править]суммесли
- •[Править]счётесли
- •Описание
- •Синтаксис
- •Замечания
- •15Статистическая проверка гипотез
- •14. Свойства дисперсии
- •Простейшие свойства математического ожидания
- •Математическое ожидание преобразования случайной величины
- •[Править]Определение
- •[Править]Свойства выборочного среднего
- •1.1.Генеральная средняя.
14. Свойства дисперсии
1. Если все значения признака уменьшить (увеличить) на одну и ту же постоянную величину, то дисперсия от этого не изменится. 2. Если все значения признака уменьшить (увеличить) в одно и то же число раз n, то дисперсия соответственно уменьшится (увеличить) в n^2 раз.
13.
1. Простая дисперсия (для несгруппированных данных) вычисляется по формуле:
![]()
2. Взвешенная дисперсия (для вариационного ряда):
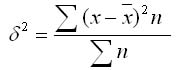
где n - частота (повторяемость фактора Х)
12.
Диспе́рсия
случа́йной величины́ —
мера разброса данной случайной
величины,
то есть её отклонения от математического
ожидания.
Обозначается ![]() в
русской литературе и
в
русской литературе и ![]() (англ. variance)
в зарубежной. В статистике часто
употребляется обозначение
(англ. variance)
в зарубежной. В статистике часто
употребляется обозначение ![]() или
или ![]() .
Квадратный корень из дисперсии, равный
.
Квадратный корень из дисперсии, равный ![]() ,
называется среднеквадрати́чным
отклоне́нием, станда́ртным
отклоне́нием или
стандартным разбросом. Стандартное
отклонение измеряется в тех же единицах,
что и сама случайная величина, а дисперсия
измеряется в квадратах этой единицы
измерения.
,
называется среднеквадрати́чным
отклоне́нием, станда́ртным
отклоне́нием или
стандартным разбросом. Стандартное
отклонение измеряется в тех же единицах,
что и сама случайная величина, а дисперсия
измеряется в квадратах этой единицы
измерения.
Из неравенства Чебышева следует, что случайная величина удаляется от её математического ожидания на более чем k стандартных отклонений с вероятностью менее 1/k². Так, например, как минимум в 75 % случаев случайная величина удалена от её среднего не более чем на два стандартных отклонения, а в примерно 89 % — не более чем на три.
11.
Математи́ческое
ожида́ние — среднее
значение случайной
величины,
распределение вероятностей случайной
величины, рассматривается в теории
вероятностей.[1] В
англоязычной литературе и в математическом
сообществе Санкт-Петербурга обозначается
через ![]() (например,
от англ. Expected
value или нем. Erwartungswert),
в русской —
(например,
от англ. Expected
value или нем. Erwartungswert),
в русской — ![]() (возможно,
от англ. Mean
value или нем. Mittelwert,
а возможно от рус. Математическое
ожидание).
В статистике часто используют
обозначение
(возможно,
от англ. Mean
value или нем. Mittelwert,
а возможно от рус. Математическое
ожидание).
В статистике часто используют
обозначение ![]() .
.
Простейшие свойства математического ожидания
Математическое ожидание числа есть само число.
![]()
![]() —
константа;
—
константа;
Математическое ожидание линейно, то есть
![]() ,
,
где ![]() —
случайные величины с конечным
математическим ожиданием, а
—
случайные величины с конечным
математическим ожиданием, а ![]() —
произвольные константы;
—
произвольные константы;
Математическое ожидание сохраняет неравенства, то есть если
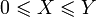 почти
наверное,
и
почти
наверное,
и 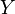 —
случайная величина с конечным
математическим ожиданием, то математическое
ожидание случайной величины
—
случайная величина с конечным
математическим ожиданием, то математическое
ожидание случайной величины 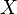 также
конечно, и более того
также
конечно, и более того
![]() ;
;
Математическое ожидание не зависит от поведения случайной величины на событии вероятности нуль, то есть если
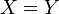 почти
наверное,
то
почти
наверное,
то
![]() .
.
Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий
![]() .
.
10.
Математическое ожидание преобразования случайной величины
Пусть ![]() — борелевская
функция,
такая что случайная величина
— борелевская
функция,
такая что случайная величина ![]() имеет
конечное математическое ожидание. Тогда
для него справедлива формула:
имеет
конечное математическое ожидание. Тогда
для него справедлива формула:
![]() ,
,
если имеет дискретное распределение;
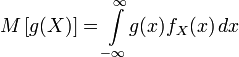 ,
,
если имеет абсолютно непрерывное распределение.
Если распределение ![]() случайной
величины
общего
вида, то
случайной
величины
общего
вида, то
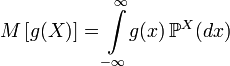 .
.
В
специальном случае, когда ![]() ,
Математическое ожидание
,
Математическое ожидание ![]() называется
называется
![]() -тым
моментом случайной
величины.
-тым
моментом случайной
величины.
9.
ЗАКОН РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ [ distribution of discrete random variable ]
Законом распределения дискретной случайной величины называют перечень всех возможных ее значений и ихвероятностей. Обычно закон распределения задается в виде таблицы, одна графа которой содержит все возможные значения случайной величины, а вторая - соответствующие им вероятности: X : x1, x2 ,..., xn; P : p1, p2 ,..., pn. Представление закона распределения возможно также в виде формулы, посредством параметров или в виде графика.
8.
Генеральная дисперсия.
Для того чтобы охарактеризовать рассеяние значений количественного признака Х генеральной совокупности вокруг своего среднего значения, вводят сводную характеристику — генеральную дисперсию.
![]() Генеральной
дисперсией Dг называют
среднее арифметическое квадратов
отклонений значений признака генеральной
совокупности от их среднего значения .
Генеральной
дисперсией Dг называют
среднее арифметическое квадратов
отклонений значений признака генеральной
совокупности от их среднего значения .
Если все значения признака генеральной совокупности объема N различны, то
![]()
Если же значения признака имеют соответственно частоты N1, N2, …, Nk, где N1 +N2+…+Nk= N, то
![]()
Кроме дисперсии для характеристики рассеяния значений признака генеральной совокупности вокруг своего среднего значения пользуются сводной характеристикой— средним квадратическим отклонением.
7.
Вы́борочное (эмпири́ческое) сре́днее — это приближение теоретического среднего распределения, основанное на выборке из него.
