1.4.1. Теоретическая часть

• Алгоритм решение дифференциального уравнения n-го порядка 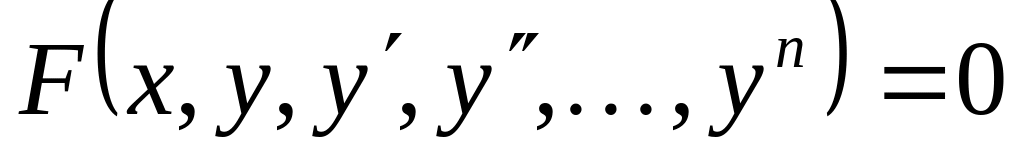на отрезке x[a;b] при начальных условиях y₀=y(x₀), y′₀=y′(x₀),…, y^n-1₀=y^n-1(x₀) методом Рунге-Кутта четвертого порядка (Задача Коши).

• Исходное уравнение сведем к системе дифференциальных уравнений 1-го порядка, введя обозначение y=z. Тогда получим систему следующего вида:

• На каждом шаге воспользуемся формулами интегрирования по методу Рунге-Кутта:

y_i = y_i-1 +1/6(k₁ +2k₂ +2k₃ + k₄ );

z_1,i = z_1,i-1+1/6(l₁ +2l₂ +2l₃ + l₄ );

……………………………………………

z_n-1,i = z_n-1,i-1+1/6(m₁ +2m₂ +2m₃ + m₄ );

Здесь k₁=h*f₁(x_i-1, y_i-1, z_1,i-1, …, z_n-1,i-1);

l₁=h* f₂(x_i-1, y_i-1, z_1,i-1, …, z_n-1,i-1);

……………………………………

m₁=h* f_n(x_i-1 , y_i-1 , z_1,i-1, …, z_n-1,i-1);

k₂ =h* f₁(x_i-1+h/2, y_i-1+ k₁/2, z_1,i-1+ l₁/2,…, z_n-1,i-1 + m₁/2);

l₂ =h* f₂(x_i-1+h/2, y_i-1+ k₁/2, z_1,i-1+ l₁/2,…, z_n-1,i-1 + m₁/2);

……………………………………

m₂=h* f_n(x_i-1+h/2, y_i-1 + k₁/2, z_1,i-1+ l₁/2,…, z_n-1,i-1 + m₁/2);

k₃ =h* f₁(x_i-1+h/2 , y_i-1+ k₂/2 , z_1,i-1+ l₂/2,…, z_n-1,i-1 + m₂/2);

l₃ =h* f₂(x_i-1+h/2 , y_i-1+ k₂/2 , z_1,i-1+ l₂/2,…, z_n-1,i-1 + m₂/2);

……………………………………

m₃=h* f_n(x_i-1+h/2, y_i-1 + k₂/2, z_1,i-1+ l₂/2,…, z_n-1,i-1 + m₂/2);

k₄ =h* f₁(x_i-1+h , y_i-1+ k₃ , z_1,i-1+ l₃,…, z_n-1,i-1 + m₃);

l₄ =h* f₂(x_i-1+h , y_i-1+ k₃ , z_1,i-1+ l₃,…, z_n-1,i-1 + m₃);

……………………………………

m₄=h* f_n(x_i-1+h, y_i-1 + k₃, z_1,i-1+ l₃,…, z_n-1,i-1 + m₃);

где h=(b-a)/n – шаг интегрирования, n - число шагов.

1.4.2. Практическая часть

• Постановка задачи. Решить дифференциальное уравнение 2-го порядка на отрезке [1;1,5], удовлетворяющее начальным условиям y₀ =y(1)= 5 и z₀= y(1)=z(1)= –1. На этом же отрезке вычислить точное (аналитическое) решение этого дифференциального уравнения: y=5-ln(x).

• Алгоритм решение дифференциального уравнения 2-го порядка на отрезке [a;b] при начальных условиях y₀=y(x₀) и y′₀=y′(x₀) методом Рунге-Кутта.

• Исходное уравнение сведем к системе дифференциальных уравнений 1-го порядка, введя обозначение y=z. Тогда получим систему следующего вида:

• На каждом шаге воспользуемся формулами интегрирования по методу Рунге-Кутта:

y_i = y_i-1 +1/6(k₁ +2k₂ +2k₃ + k₄ );

zi = z_i-1+1/6(l₁ +2l₂ +2l₃ + l₄ ) ,

Здесь k₁=h*f(x_i-1 , y_i-1 , z_i-1);

l₁=h*g(x_i-1 , y_i-1 , z_i-1);

k₂ =h*f(x_i-1+h/2 , y_i-1+k₁/2 , z_i-1+l₁/2);

l₂ =h*g(x_i-1+h/2 , y_i-1+k₁/2 , z_i-1+l₁/2);

k₃ =h*f(x_i-1+h/2 , y_i-1+k₂/2 , z_i-1+l₂/2);

l₃ =h*g(x_i-1+h/2 , y_i-1+k₂/2 , z_i-1+l₂/2);

k₄ =h*f(x_i-1+h , y_i-1+k₃ , z_i-1+l₃);

l₄ =h*g(x_i-1+h , y_i-1+k₃ , z_i-1+l₃),

• Для решения дифференциального уравнения 2-го порядка модифицированным методом Эйлера следует воспользоваться формулами интегрирования:

y_i = y_i-1 +(k₁+k₂)/2 ;

z_i = z_i-1 +(l₁+l₂)/2 ,

где k₁=h*f(x_i-1 , y_i-1 , z_i-1); l₁=h*g(x_i-1 , y_i-1 , z_i-1);

k₂=h*f(x_i-1+h , y_i-1+ k₁ , z_i-1+ l₁);

l₂=h*g(x_i-1+h , y_i-1+ k₁ , z_i-1 + l₁).

• Программный код решения дифференциального уравнения 2-го порядка методом Рунге-Кутта.

Dim ymax As Double, ymin As Double

Dim xmax As Double, xmin As Double

Dim ax() As Double, ay() As Double

Dim a As Double, b As Double, n As Double

Private Function f(x As Double, y As Double, z As Double) As Double

f = z

End Function

Private Function g(x As Double, y As Double, z As Double) As Double

g = -z / x ‘Это все равно, что y″= -y′/x

End Function

Private Sub Form_Load()

ss$ = ""

a = InputBox("Нижняя граница Х",,1)

b = InputBox("Верхняя граница Х",,1.5)

n = InputBox("Число точек на границе",,10)

y0# = InputBox("Начальное зн.функции","y", 5)

z0# = InputBox("Начальное зн.производной","dy", -1)

y# = y0

z# = z0

x# = a

h# = (b - a) / n

ReDim ax(n)

ReDim ay(n)

i = 0

Do While x < b + h

yy# = 5 - Log(x)

ss = ss & "X=" & Format(x, "#0.000") & Space(5) & _

"Точ. решение = " & Format(yy, "#0.00000000") & Space(5) & _

" Y = " & Format(y, "#0.00000000") & vbCrLf

k1# = h * f(x, y, z)

i1# = h * g(x, y, z)

k2# = h * f(x + h / 2, y + k1 / 2, z + i1 / 2)

i2# = h * g(x + h / 2, y + k1 / 2, z + i1 / 2)

k3# = h * f(x + h / 2, y + k2 / 2, z + i2 / 2)

i3# = h * g(x + h / 2, y + k2 / 2, z + i2 / 2)

k4# = h * f(x + h, y + k3, z + i3)

i4# = h * g(x + h, y + k3, z + i3)

ax(i) = x : ay(i) = y

y = y + (k1 + 2 * k2 + 2 * k3 + k4) / 6

z = z + (i1 + 2 * i2 + 2 * i3 + i4) / 6

x = x + h

i = i + 1

Loop

Text1 = ss

i = 0

ymax = ay(i)

ymin = ay(i)

xmin = a

xmax = b

D

Рис.7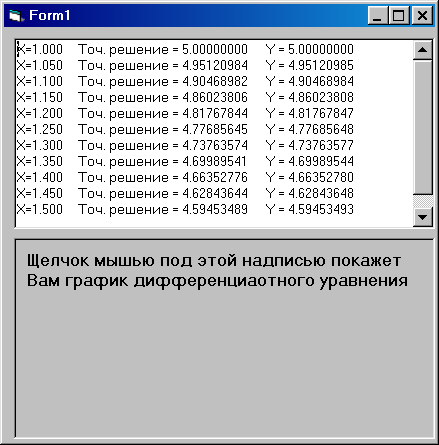

o

If ay(i) > ymax Then ymax = ay(i)

If ay(i) < ymin Then ymin = ay(i)

i = i + 1

Loop Until>UBound(ay) '>n

If ymin > 0 Then ymin = 0

If ymax < 0 Then ymax = 0

If xmin > 0 Then xmin = 0

If xmax < 0 Then xmax = 0

Picture1.Scale (xmin - 0.05, _

ymax + 0.1)-(xmax + 0.05, _

ymin - 0.1)

End Sub

Private Sub Picture1_Click()

Label1.Visible = False

Picture1.Cls

Picture1.BackColor = vbWhite

Picture1.DrawWidth = 2

Picture1.Line (xmin, ymin)-(xmax, ymin)

Picture1.Line (xmin, ymin)-(xmin, ymax) 'ОСИ: x, y

i& = 0

Picture1.DrawWidth = 3

Do 'Graphic

If i <= n - 1 Then

Picture1.Line (ax(i), ay(i))-(ax(i + 1), ay(i + 1)), vbRed

End If

i = i + 1

Loop Until i > UBound(ay)

Picture1.DrawWidth = 1

Picture1.DrawStyle = 2

For j# = xmin To xmax Step 0.5 'Grid

Picture1.Line (j, ymin)-(j, ymax), vbBlack

Next

For j# = ymin To ymax Step 0.5

Picture1.Line (xmin, j)-(xmax, j), vbBlack

Next

Picture1.FontBold = True

Picture1.CurrentX = xmin + 0.05 'Label's

Picture1.CurrentY = ymax - 0.1

Picture1.Print "Y"

Picture1.CurrentX = xmax - 0.1

Picture1.CurrentY = ymin + 0.5

Picture1.Print "X"

P

Рис.8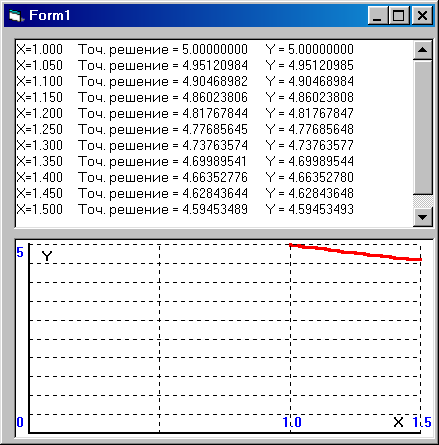

icture1.ForeColor = vbBlue

Picture1.CurrentX = xmax - 0.03

Picture1.CurrentY = ymin + 0.5

Picture1.Print Format(b, "#0.0")

Picture1.CurrentX = xmax - 0.53

Picture1.CurrentY = ymin + 0.5

Picture1.Print Format(a, "#0.0")

Picture1.CurrentX = xmin - 0.05

Picture1.CurrentY = ymax - 0.01

Picture1.Print Format(ymax,"#0")

Picture1.CurrentX = xmin - 0.05

Picture1.CurrentY = ymin + 0.5

Picture1.Print Format(ymin,"#0")

End Sub