11.2. Структура систем управления запасами.
Рассмотрим обобщённую структуру системы управления запасами в типичной системе (рис.11.2.1б).
Рис. 11.2.1. Кривая изменения запаса в типичной системе.
Здесь, приведена схема, иллюстрирующая динамику управления запасами в типичной системе. Такие системы описываются уравнением, связывающим запас в момент времени t с запасом в некоторый, более поздний момент t‘.
Пусть It есть запас в момент времени t, а S — пополнение запаса на интервале времени от t до t‘ и D — спрос.
Физический уровень запаса в момент t‘ определяется уравнением:
(11.2.1)
Притом, должно выполняться условие, что запас не падает до нуля.
Если спрос будет превышать предложение, то физический уровень запаса станет равен нулю.
С точки зрения учета, возможны две ситуации. Если избыточный спрос учитывается как невыполненные заказы и удовлетворяется, как только появляется необходимое количество товаров, то невыполненные заказы можно рассматривать как отрицательный запас, и уравнение (11.2.1) выполняется при любых значениях It , S и D. В большинстве задач управления запасами управляемой переменной является величина пополнения запаса S.
50
В ходе решения задачи определяют оптимальные значения этой переменной и оптимальные моменты времени пополнения запаса. Иногда появляется возможность регулирования спроса D или некоторых параметров, характеризующих эту величину.
Однако принципиальная схема, иллюстрирующая необходимое условие для осуществления единичного действия по использованию запаса не позволяет учитывать динамику процесса и разнообразие ситуаций.
Обратимся к следующей схеме (рис. 11.2.2.).
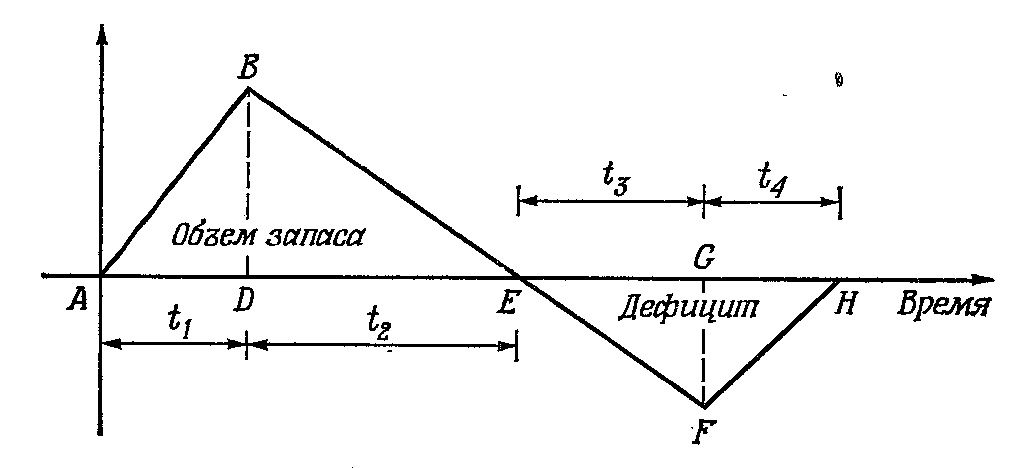
Р и с. 11.2.2. Цикл изменения запаса.
Как видно из рис. 11.2.2, существует цикл изменения запаса. Начальный запас равен нулю, а его возрастание продолжается в течение периода t1.
Затем он уменьшается в течение периода t2, пока не достигнет нуля. С этого момента начинается накопление невыполненных заказов, то есть, происходит рост дефицита. Это продолжается в течение периода t3 .
В конце этого периода вновь начинается производство, и дефицит уменьшается в течение периода t4 , в конце которого дефицит ликвидируется (становится равным нулю).
Затем этот цикл, имеющий общую продолжительность t1+t2+t3+t4 повторяется.
Из рисунка 11.2.2. видно, что общие затраты на хранение запаса определяются величиной c1, умноженной на площадь треугольника АВЕ. Высота BD этого треугольника определяет максимальный запас, обозначаемый символом S, а его основание АЕ равно (t1 + t2).
Таким образом, затраты на хранение запаса равны:
(11.2.2)
Общие потеря от дефицита равны величине с2, умноженной на площадь треугольника EFH Высота GF этого треугольника определяет максимальный дефицит, обозначаемый символом s, а основание равно (t3 + t4).
Следовательно, потери от дефицита определяются формулой:
(11.2.3.).
Если сложить потери от дефицита с затратами на хранение и с затратами на подготовку производства и разделить полученную сумму на общую
51
продолжительность цикла t1+t2+t3+t4 , то получим средние затраты в единицу времени К, определяемые следующим выражением:
(11.2.4.).
Минимизация численного значения К представляет достаточно громоздкую процесс, связанный, вдобавок, еще и преобразованиями по сокращения числа переменных.
В реальных условиях, стараются сократить вычислительную часть задачи, предварительно уточнив влияние тех факторов, которые являются наиболее важными для принятия решений. А если сказать точнее, то нас, прежде всего, интересуют переменные, которыми можно управлять.
Запас состоит из годных к употреблению, но не используемых ресурсов. В качестве ресурсов могут выступать, например, люди, материалы, машины или деньги.
Если рассматриваемым ресурсом является материал или изделие в любой степени готовности, то запас обычно называют «резервом».
Задача о запасе возникает при условии, когда количество ресурсов можно регулировать и когда существует, по крайней мере, одна статья затрат, убывающих при увеличении запаса.
Как правило, целевая функция в задачах такого рода сводится к минимизации общих (фактических или ожидаемых) затрат.
Однако если запас оказывает влияние на спрос (т. е. на объем ресурса, требующийся потребителю), то целевая функция может выражаться в максимизации (фактической или ожидаемой) прибыли.
К управляемым переменным в задачах о запасах, которые можно изменять независимо или совместно, относятся:
1. Поступающий объем ресурсов (в результате закупки, производства или с помощью каких-либо иных средств). Вопрос заключается в том, сколько приобрести, выпустить и т. п. Этот показатель может определяться для ресурса каждого вида по отдельности или же для целого набора ресурсов.
2. Частота или сроки поступления ресурсов, т. е. управляемыми переменными являются периодичность и моменты времени поступления ресурсов. Руководитель может иметь возможность регулировать эти управляемые переменные, принадлежащие к одной или обеим категориям.
З. Степень готовности продукции, хранящейся в виде запасов.
Чем выше степень готовности запасаемой продукции, тем меньше запаздывание в удовлетворении спроса на нее и тем выше затраты, связанные с созданием запаса. Чем меньше готовность продукции (в предельном случае она может быть исходным сырьем), тем больше времени требуется на выполнение заказов, но тем ниже стоимость содержания запаса.
Неуправляемые переменные в задачах о запасах можно разделить на стоимостные и прочие.
К основным переменным каждого вида относятся: