- •18. Дифференциальные уравнения с частными производными
- •18.1. Классификация дифференциальных уравнений с частными производными
- •18.2. Методы решения уравнений с частными производными.
- •18.3. Классификация уравнений математической физики (линейных дифференциальных уравнений с частными производными второго порядка)
- •18.4. Краевые условия
- •18.5. Постановка краевых задач для уравнения параболического типа
- •18.6. Решение дифференциального уравнения параболического типа (уравнения теплопроводности).
18.6. Решение дифференциального уравнения параболического типа (уравнения теплопроводности).
Применяя метод Фурье (разделения переменных), можно получить решение задачи Коши для следующих трёх случаев:
1.
Случай бесконечного стержня. Постановка
задачи о нахождении решения
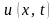 уравнения
уравнения
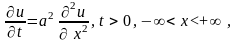 удовлетворяющего
удовлетворяющего
начальному
условию
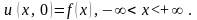
Решение уравнения имеет вид:
 . Эта формула
называемая интегралом Пуассона
представляет собой решение задачи о
распространении тепла в неограниченном
стержне.
. Эта формула
называемая интегралом Пуассона
представляет собой решение задачи о
распространении тепла в неограниченном
стержне.
2. Случай полубесконечного стержня. Если участок стержня, температуру которого нам надо найти, находится вблизи одного конца и далеко от другого, то температура практически определяется температурным режимом близкого конца
(0 ≤ х
< +∞) и начальными условиями. Постановка
задачи: найти решение уравнения
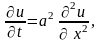 удовлетворяющее
начальному условию
удовлетворяющее
начальному условию
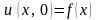 (0 < х
< +∞) и краевому условию
(0 < х
< +∞) и краевому условию
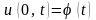 ,
t
≥ 0. Решение имеет вид:
,
t
≥ 0. Решение имеет вид:
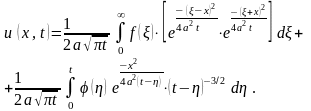
3.
Случай стержня конечной длины. Пусть
длина стержня равна l.
Выберем начало координат на левом конце
стержня, тогда его торцевые сечения
будут
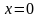 и
и
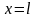 .
В данном случае задача Коши состоит в
том, чтобы найти решение уравнения
удовлетворяющее
начальному условию
.
В данном случае задача Коши состоит в
том, чтобы найти решение уравнения
удовлетворяющее
начальному условию
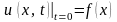 ( 0≤ х ≤ l
) и краевым условиям, например
( 0≤ х ≤ l
) и краевым условиям, например
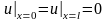 (на обоих концах поддерживается постоянная
температура) или
(на обоих концах поддерживается постоянная
температура) или
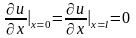 (оба конца стержня теплоизолированы.
Тогда частное решение ищется в виде
ряда:
(оба конца стержня теплоизолированы.
Тогда частное решение ищется в виде
ряда:
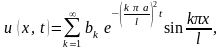
где
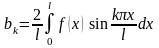
(для краевых условий ); и в виде ряда:
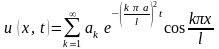
где
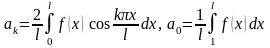
(для краевых условий ).
Задача. Найти
закон распределения температуры в
длинном однородном стержне, боковая
поверхность которого теплоизолирована,
а начальное распределение температуры
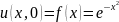 .
.
Решение. Если пренебречь влиянием температурных условий на концах длинного стержня, то можно считать его бесконечным. В этом случае получаем задачу Коши: решение уравнения
которое удовлетворяло бы начальному условию
.
Решение запишем в виде интеграла Пуассона
По
условию задачи
 поэтому
поэтому