
- •Лекция №2.
- •Лекция №3. Абсолютные и относительные величины.
- •Средние величины.
- •Средняя арифметическая величина.
- •Лекция №4 Математические свойства средней арифметической величины.
- •Расчет средней арифметической величины способом моментов.
- •Средняя гармоническая величина.
- •Средняя геометрическая величина.
- •Средняя квадратическая величина.
- •Структурные средние величины.
- •Лекция № 5
- •Показатели вариации.
- •Лекция №6.
- •Математические свойства дисперсии.
- •Расчет дисперсии способом моментов.
- •Расчет дисперсии методом средних.
- •Правила сложения дисперсии.
- •Дисперсия альтернативного признака.
- •Лекция №7 Выборочное наблюдение.
- •Лекция №8. Ряды динамики.
- •Расчет среднего уровня в рядах динамики.
- •Основные аналитические и средние показатели рядов динамики.
- •Лекция №9.
- •Лекция №10 Экономические индексы.
- •Лекция №11 Средние экономические индексы.
- •Индексы средних величин.
- •Лекция №12. Корреляционно-регрессивный анализ (кра).
- •Лекция №13.
- •Изучение степени тесноты между двумя качественными признаками.
Средняя геометрическая величина.
Еще одной формулой, по которой может осуществляться расчет среднего показателя, является средняя геометрическая величина:
Невзвешенная (простая):
 ,
,Взвешенная:
 .
.
Наиболее широкое применение этот вид средней получил в анализе динамики для определения среднего темпа роста.
Средняя квадратическая величина.
В основе вычисления ряда сводных расчетных показателей лежит средняя квадратическая:
Невзвешенная (простая):
 ;
Взвешенная:
;
Взвешенная:
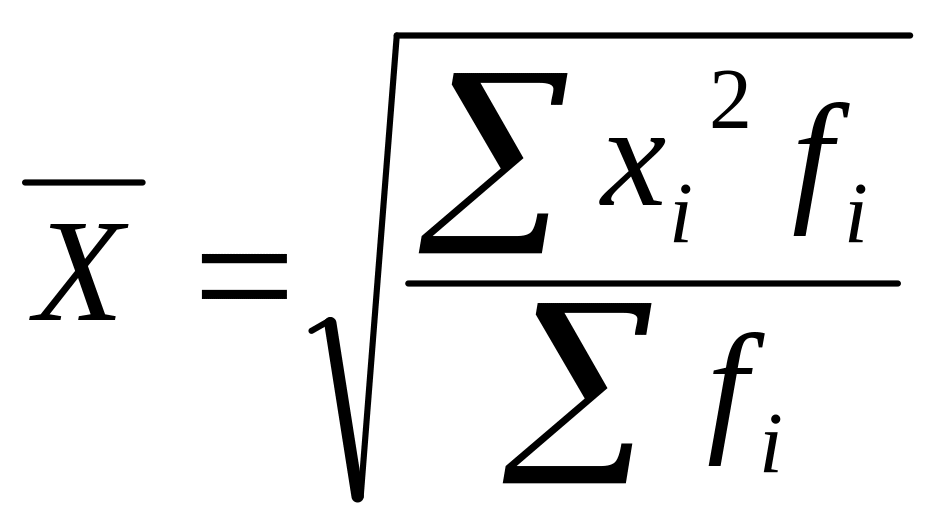 .
.
Наиболее широко этот вид средней используется при расчете показателей вариации.
Структурные средние величины.
К структурным средним величинам относятся:
Мода (Мо)
Медиана (Ме)
Квартили (Q)
Децили (D)
Все средние структурные являются именованными величинами и выражаются в тех же единицах измерения, что и значения признака (варианты).
1. Модей в статистике называют значение признака (вариант), который наиболее часто встречается в исходной совокупности. В дискретном вариационном ряду Мо является вариант, имеющий наибольшую частоту. Рассмотрим на примере с семьями:
Число детей |
Количество семей |
Х |
ƒ
|
0 |
3 |
1 |
8 |
2 |
4 |
3 |
3 |
4 |
2 |
Итого |
20 |
В этом примере наибольшей частоте 8 соответствует значение признака – 1 ребенок, это и есть значение Мо и, следовательно, наиболее часто встречаются в данном примере семьи, имеющие одного ребенка.
В интервальном вариационном ряду с
равными интервалами по наибольшей
частоте (частости) находят интервал,
содержащий Мо (модальный интервал)
и далее Мо вычисляют по формуле:
![]() , где:
, где:
![]() -
нижняя граница интервала, содержащая
Мо; iMo
– величина модального интервала; fMo
– частота модального интервала;
-
нижняя граница интервала, содержащая
Мо; iMo
– величина модального интервала; fMo
– частота модального интервала;
![]() - частота интервала, предшествующего
модальному;
- частота интервала, предшествующего
модальному;
![]() - частота интервала, следующего за
модальным. Пример:
- частота интервала, следующего за
модальным. Пример:
Возраст депутата (полных лет) (X) |
Численность депутатов (кол-во человек) (ƒ)
|
20-29 |
1 |
30-39 |
16 |
40-49 |
28 |
50-59 |
30 |
60-69 |
7 |
Итог: |
82 |
В интервальном вариационном ряду Мо можно также вычислить графически по гистограмме:

В интервальном вариационном ряду с неравными интервалами для определения Мо необходимо:
рассчитать частости W
вычислить плотность распределения путем деления частости на величину соответствующего интервала: Z=W/i.
по наибольшей плотности распределения найти модальный интервал
Мо вычислить по формуле:

В интервальном вариационном ряду с неравными интервалами Мо можно вычислить графически по гистограмме. Для этого по оси ординат вместо частот откладываются соответствующие плотности распределения.
