Лекция №8. Ряды динамики.
Одной из задач статистики является изучение изменения социально-экономических явлений и процессов во времени. Эта задача решается с помощью составления и анализа рядов динамики.
Ряд динамики представляет собой последовательность числовых значений изучаемого статистического показателя за определенные периоды времени. Числовые значения, составляющие ряд динамики называются уровнями ряда и обозначаются yi (i=1,2,…,n). В зависимости от вида показателей, составляющих ряд динамики, различают ряды абсолютных, относительных и средних величин. Уровни ряда динамики могут относиться к определенным моментам или периодам времени. В зависимости от этого ряды динамики подразделяются на моментные и интервальные.
Моментным называют ряд динамики, уровни которого характеризуют величину изучаемого показателя на определенный момент времени (на конкретную дату). Например: приводится численность населения Российской Федерации (млн. чел.): на 01.01.1999 – 146,3; на 01.01.2000 – 145,6; на 01.01.2001 – 144,8; на 01.01.2002 – 144,0; на 01.01.2003 -145,2.
Интервальным называют ряд динамики, уровни которого характеризуют величину изучаемого показателя за определенный период времени. Например: приводится объем кредитных вложений в экономику страны: 2000 г. – 808; 2001 г. – 1286; 2002 г. – 1755.
Расчет среднего уровня в рядах динамики.
Различают: y1 -
начальный уровень ряда, yn
– конечный уровень ряда,
-
средний уровень ряда. В моментном ряду
динамики возможны следующие варианты
расчета среднего уровня:
Если приводятся данные только на начало и на конец изучаемого периода, то средний уровень рассчитывается, как средняя арифметическая величина из этих двух значений.
Если моменты времени, к которым относятся уровни ряда расположены через равные промежутки, то средний уровень определяется по формуле простой хронологической средней:
,
где n – число уровней
ряда.
Если моменты времени, к которым относятся уровни ряда расположены через не равные промежутки, то средний уровень рассчитывается по формуле хронологической взвешенной:
,
где
- полусумма двух соседних уровней ряда;
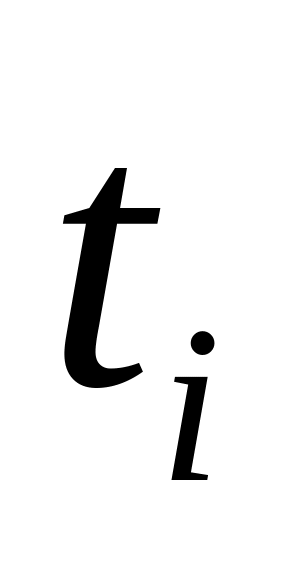- промежуток между двумя соседними
уровнями ряда, выраженный в днях, месяцах
и т. д. в зависимости от исходных данных.
В интервальном ряду динамики средний уровень рассчитывается следующим образом:
1. В ряду с равноотстоящими интервалами
по формуле простой арифметической
средней:
.
2. В ряду с не равноотстоящими интервалами по формуле средней арифметической
взвешенной:
.
Основные аналитические и средние показатели рядов динамики.
Кроме среднего уровня для анализа рядов динамики вычисляют следующие аналитические показатели:
Абсолютный прирост (
)Коэффициент роста (Кр)
Темп роста (Тр)
Темп прироста (Тпр)
Абсолютное значение 1% прироста (Аi)
Возможны 2 варианта сравнения уровней рядов динамики. При 1-ом варианте сравнения каждый i-ый уровень ряда сравнивают с каким-то первым уровнем, выбранным в качестве базы сравнения. Как правило, в качестве базы сравнения выбирают уровень начального периода. Полученные в результате сравнения показатели называются базисными и характеризуют изменение изучаемого показателя в данном периоде, по сравнению с начальным периодом. При втором варианте сравнения каждый i-ый уровень ряда сравнивают с предшествующим уровнем, т. е. база сравнения все время меняется. Рассчитанные при этом варианте показатели называются цепными и характеризуют изменение изучаемого показателя в данном периоде по сравнению с предшествующим.
1) Абсолютный прирост показывает на сколько единиц изменится уровень данного периода, по сравнению с уровнем, выбранным в качестве базы сравнения.
Базисные показатели:
;
цепные показатели:
.
2) Коэффициент роста показывает, во сколько раз изменился уровень данного периода по сравнению с уровнем, выбранным в качестве базы сравнения.
(б.)
(ц.)
3) Темп роста представляет собой коэффициент роста, выраженный в процентах (%):
(б.)
(ц.)
4) Темп прироста характеризует относительное изменение уровней ряда, выраженное в %:
(б.)
(ц.)
5) Абсолютное значение 1% прироста
показывает на сколько единиц изменился
уровень ряда динамики при его изменении
на 1%:
.
Кроме перечисленных аналитических показателей вычисляют средние показатели динамики за определенный период времени. Вычисляют:
1) среднегодовой абсолютный прирост,
который показывает на сколько единиц
изменялись уровни ряда динамики ежегодно,
в течение определенного периода времени:
,
где m – число цепных
абсолютных приростов.
2) среднегодовой коэффициент роста, который показывает, во сколько раз ежегодно изменялись уровни ряда динамики в течение определенного периода времени:
3) среднегодовой темп роста представляет
собой среднегодовой коэффициент роста,
выраженный в процентах (%):
.
среднегодовой темп прироста показывает на сколько процентов ежегодно изменялись уровни ряда динамики в течение определенного периода времени:
.