Розділ іі. Рівняння руху рідини в циліндричній системі координат
Рівняння руху рідини в циліндричній системі координат матимуть наступний вигляд:
|
(2.1) |
;
|
(2.2) |
;
|
(2.3) |
|
(2.4) |
;
|
(2.5) |
(ф.5.14 в 12)
Розділ ііі. Практична частина
TITLE
'В'язка течія в трубі при високих числах Рейнольдса'
SELECT
stages=3 {Вказуємо 3 етапи}
COORDINATES
ycylinder('r','z') {Використовуємо циліндричні координати з радіальною координатою “r” і осьовою координатою “z”}
VARIABLES {Задаємо змінні}
vr(0.01) vz {Координати вектора}
p {Тиск}
DEFINITIONS
L=2.0 {Довжина}
r1=1.0 {Радіус}
visc=1.0 {В’язкість}
dens=1e3 {Густина}
delp = staged(1e-6,1e-2,1,10, 20) { Послідовні значення }
k = staged(0,1,1,1,1) { Лінійні до нелінійних }
v = vector( vr, vz) {Вектор}
vm = magnitude( v) { Скалярна величина вектора }
Re = dens* globalmax(vm)*r1/ visc
div_v = 1/r*dr(r*vr)+dz(vz)
curl_phi = dz(vr)-dr(vz)
vz_ex = delp/(L* 4*visc)*(r1^2-r^2) { Точне рішення для Re<<1 }
unit_r = vector(1,0) unit_z = vector(0,1)
vrdvr = vr*dr(vr)+vz*dz(vr) vrdvz = vr*dr(vz)+ vz*dz(vz)
natp = visc*normal(unit_r)*[1/r*dr(r*dr(vr))-vr/r^2+dzz(vr)]+ +visc*normal(unit_z)*[1/r*dr(r*dr(vz))+dzz(vz)]-k*dens*[normal(unit_r)* *vrdvr+normal( unit_z)*vrdvz]
EQUATIONS
vr: k*dens* vrdvr+ dr(p)- visc*[1/r*dr(r*dr(vr))-vr/r^2+dzz(vr)]=0
vz: k*dens* vrdvz+ dz(p)- visc*[ 1/r*dr(r*dr(vz))+ dzz(vz)]= 0
p: 1/r*dr( r*dr(p))+ dzz(p)+ k*dens*[1/r*dr(r*vrdvr)+dz( vrdvz)]--1e4*visc/L^2* div_v= 0
BOUNDARIES
region 'domain' start 'outer' (0,0)
value(vr)=0 natural(vz)= 0 value(p)=delp line to (r1,0) { Вхід }
value(vr)=0 value(vz)=0 natural(p)= natp line to (r1,L)
value(vr)=0 natural(vz)=0 value(p)=0 line to (0,L) { Вихід }
value(vr)=0 natural(vz)= 0 natural(p)=0 line to close
PLOTS
contour( vz) report( Re) contour( vr)
contour( p) painted {заливка між контурами} vector( v) norm
elevation(vz, vz_ex) from (0,L) to (r1,L) report( Re) {вивід графіка в області}
elevation( 2*pi*r*vz) from (0,0) to (r1,0) { Потік }
elevation( 2*pi*r*vz) from (0,L) to (r1,L)
END
Всі одиниці використовувані в дипломній роботі задані в системі СІ.
Далі наведені результати виконання програмного коду в системі FlexPDE. Результати представлені у вигляді графіків.
Мал.2.
Напрям руху рідини
На Мал.2 зображена кінцева область зміни вектора «v», який показує напрям руху течії води в циліндричній трубі радіуса 1 і довжиною 2 і межі зміни вектора «v» які показую швидкість течій.
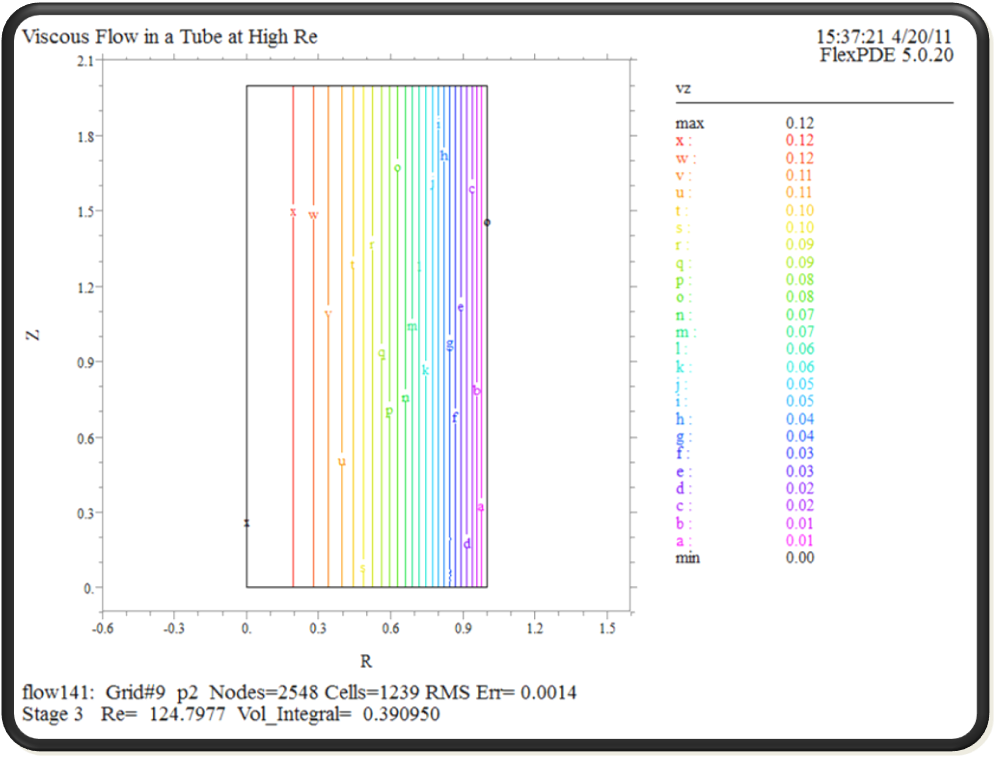Мал.3
Кінцевий розподіл швидкості рідини
На Мал.3 зображено кінцевий розподіл швидкості рідини(води) у трубі радіуса 1 і довжиною 2 по осьовій координаті «z».
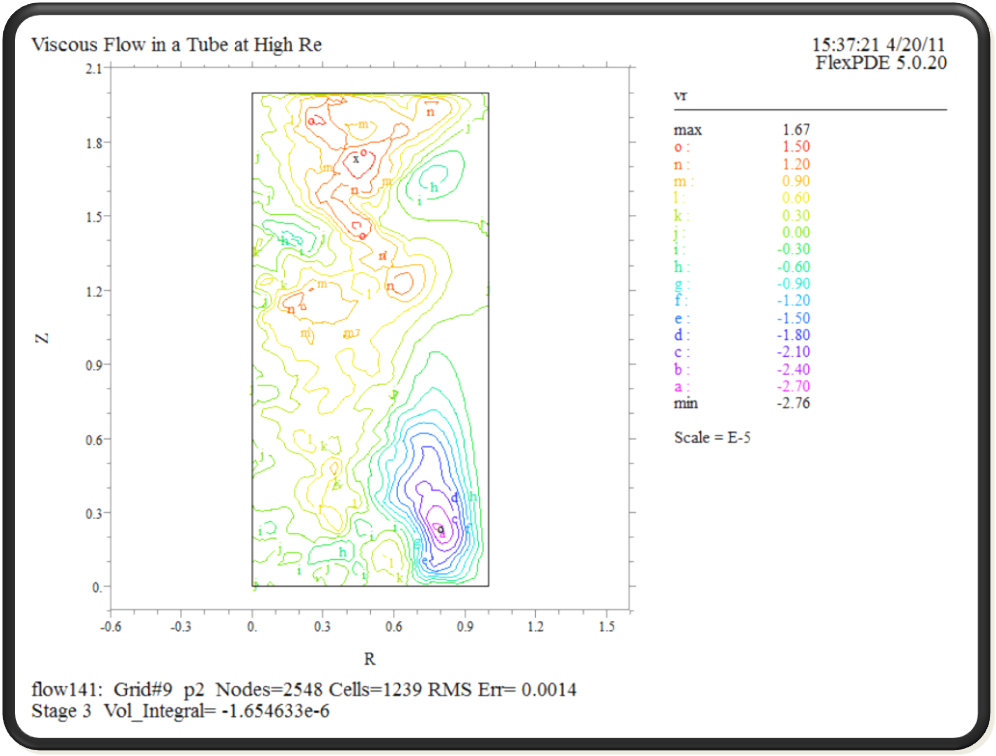Мал.4
Кінцевий розподіл швидкості рідини
На Мал.4 зображено кінцевий розподіл швидкості рідини(води) у трубі радіуса 1 і довжиною 2 по радіальній координаті «r».
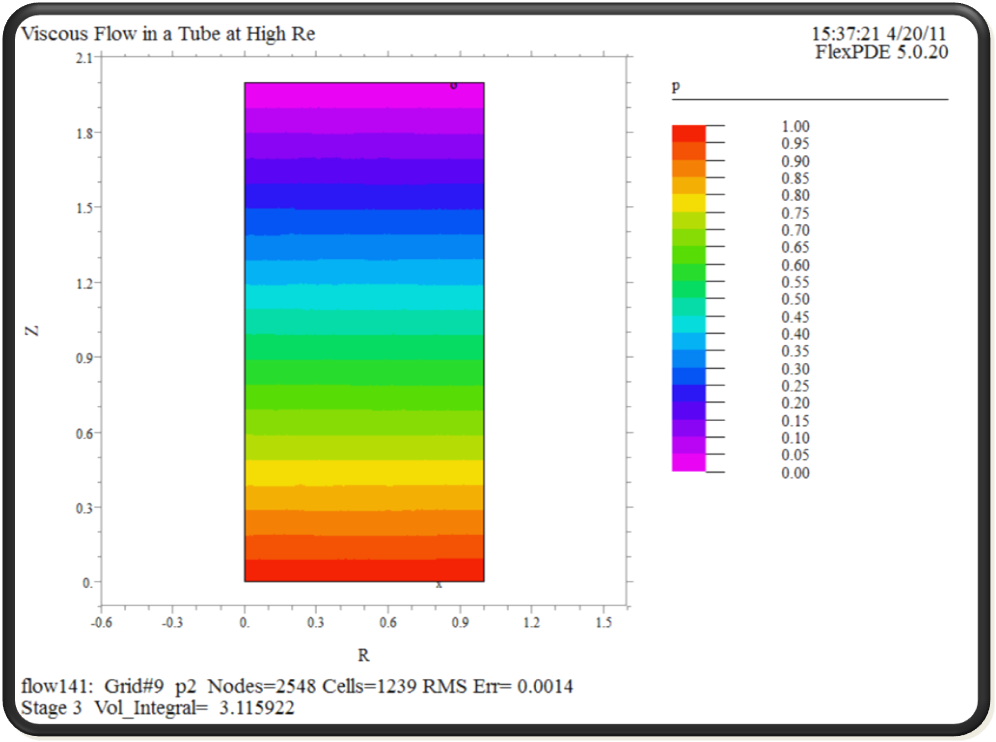Мал.5
Кінцевий розподіл тиску в системі
На Мал.5 зображено кінцевий розподіл тиску рідини(води) у трубі радіуса 1 і довжиною 2.
Програма описана вище розглядалася для течії води у трубі з радіусом 1 і довжиною 2 Змінимо параметр довжина на 10 і проведемо обрахунок ще раз.
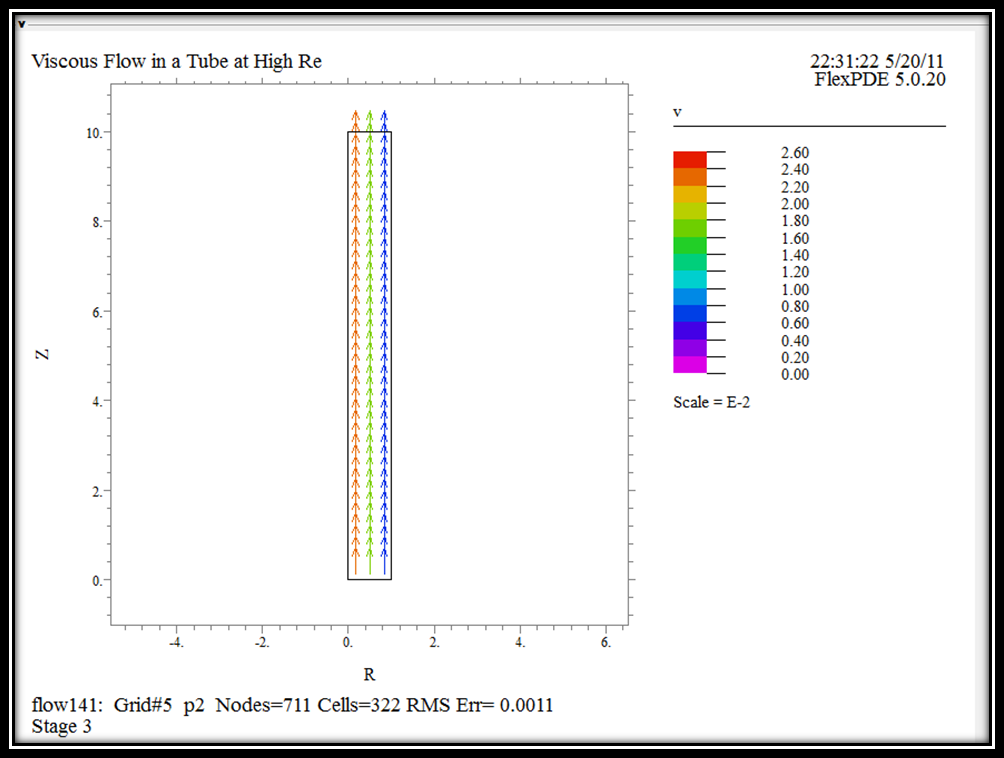
Мал.6. Напрям руху рідини
На Мал.6 зображена кінцева область зміни вектора «v», який показує напрям руху течії води в циліндричній трубі радіуса 1 і довжиною 10 і межі зміни вектора «v» які показую швидкість течій.
М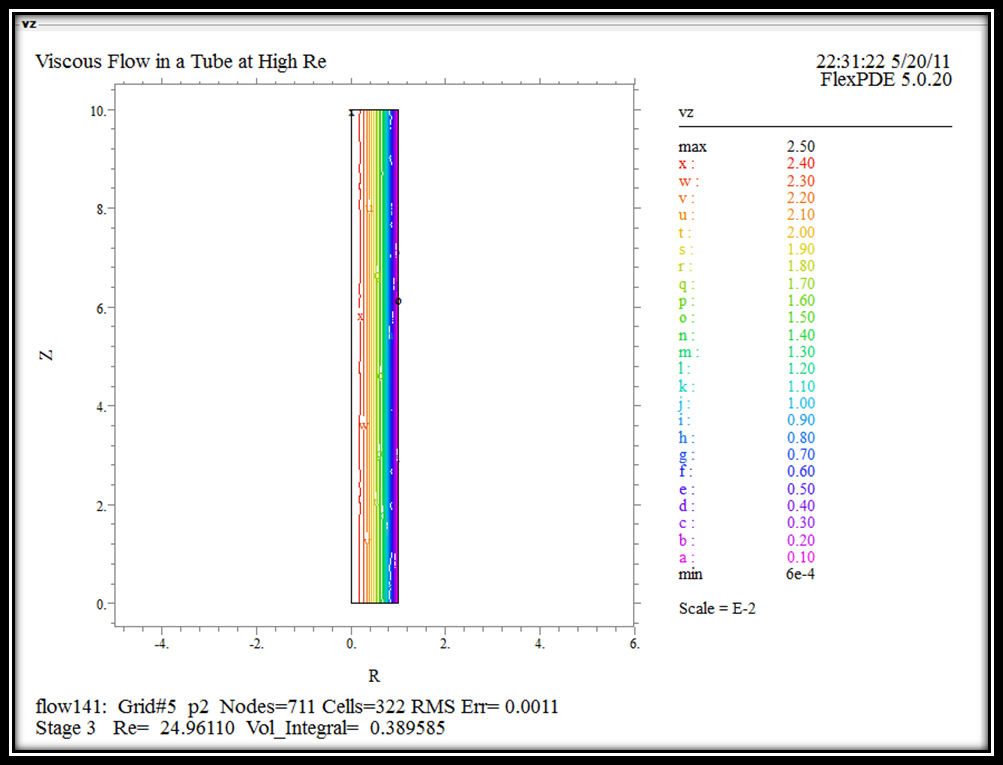
ал.7
Кінцевий розподіл швидкості рідини
На Мал.7 зображено кінцевий розподіл швидкості рідини(води) у трубі радіуса 1 і довжиною 10 по осьовій координаті «z».
Мал.8 Кінцевий розподіл швидкості рідини
На Мал.8 зображено кінцевий розподіл швидкості рідини(води) у трубі радіуса 1 і довжиною 10 по радіальній координаті «r».
Програма описана вище розглядалася для течії води у трубі з радіусом 1 і довжиною 10. Тепер розглянемо рух іншої рідини(наприклад меду) в цій самій трубі з радіусом 1 і довжиною 10 для цього потрібно змінити значення густини на 1420 і в’язкість на 9
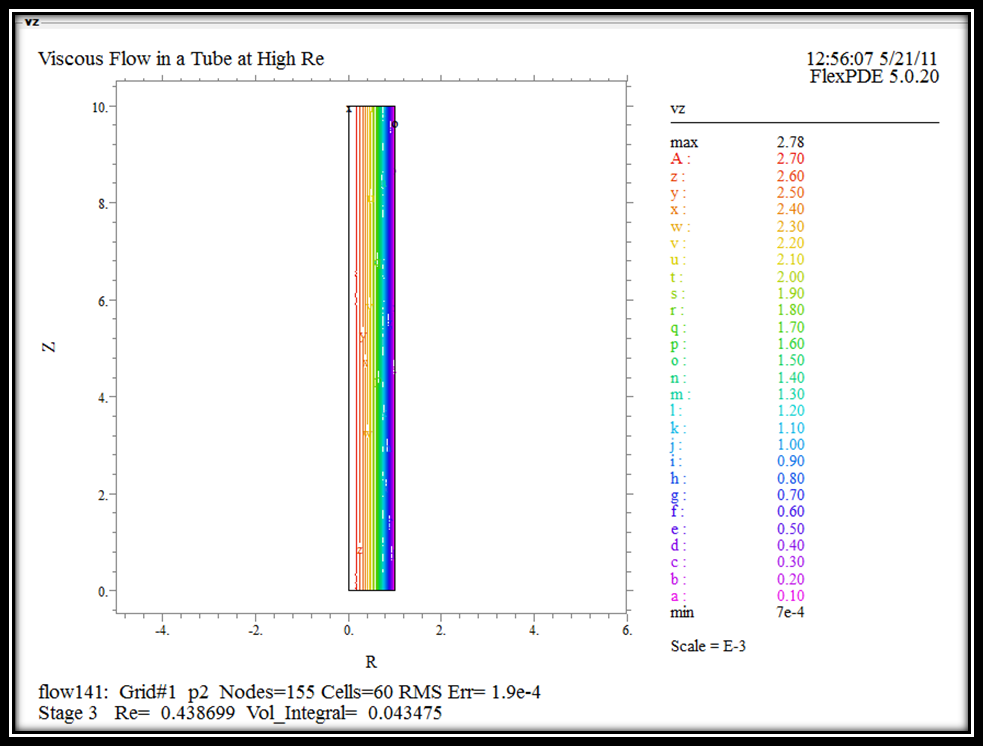
Мал.9 Кінцевий розподіл швидкості рідини
На Мал.9 зображено кінцевий розподіл швидкості рідини(Меду з густиною 1420 і в’язкістю 9) у трубі радіуса 1 і довжиною 10 по осьовій координаті «z».
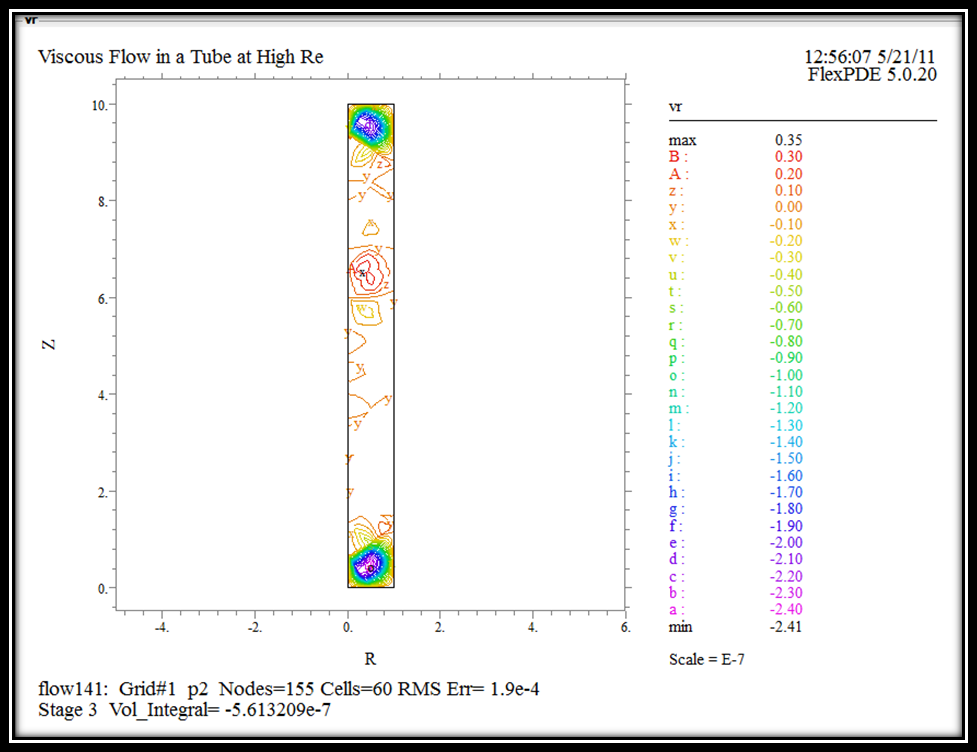
Мал.10 Кінцевий розподіл швидкості рідини
На Мал.10 зображено кінцевий розподіл швидкості рідини(Меду з густиною 1420 і в’язкістю 9) у трубі радіуса 1 і довжиною 10 по радіальній координаті «r».