3 Звіт з лабораторної роботи

3.1 Оформлюється кожним студентом індивідуально за загальними вимогами.

3.2 Звіт повинен містити: мету, завдання, основні теоретичні положення про головні особливості кристалів, їх елементів огранювання та внутрішньої будови, що визначає їх симетрію (особливу увагу необхідно звернути: на основні виводи 32 видів симетрії, основні закони кристалічних багатогранників, основні способи класифікації їх за симетрією), порядок виконання лабораторної роботи, результати власних досліджень згідно з отриманим варіантом, висновки та перелік літературних джерел, який був використаний при виконанні даної роботи.

3.3 Звіт захищається кожним студентом за системою контрольних питань.

Питання для самоперевірки

1 Назвіть головні елементи симетрії кристалів?

2 Що є кристал?

3 Чи пов’язані між собою одиничні напрямки та вісі симетрії в кристалах?

4 Що таке вісь симетрії?

5 Що таке площина симетрії?

6 Що таке центр інверсії?

7 Які лінійні параметри кристалічної гратки кристалів Ви

знаєте?

8 Назвіть один з основних законів кристалографії?

9 На основі яких теорем визначається симетрія кристалів?

10 Що є сингонія?

11 Що є категорія?

12 Які основні принципи закладені в класифікацію симетрії

кристалів?

13 Що таке одиничний напрямок в кристалах?

14 Як можуть розміщуватися одиничні напрямки по

відношенню до елементів симетрії?

Література

1. Куровець М. Кристалографія і мінералогія. Ч.I. Кристалографія мінералів.– Л.: Світ, 1996. – 236 с.

2. Шаскольська М. Кристаллографія.-М.: „Высшая школа”, 1976.

3. Павлинов В. и др. Пособие к лабораторным занятиям по общей геологии. Учеб. Пособие для ВУЗов.-4-е изд., перераб. и доп.-М.: Недра, 1988.-149 с.

4. Попов Г., Шафроновский И. Кристаллография. Изд. 5-е. Учебник для студентов геологических специальностей высших учебных заведений. М.: „Высшая школа”, 1972.

Лабораторна робота № 2 Прості форми і комбінації та їх визначення

Мета:  навчити студента аналізу зовнішньої форми кристалів (тобто визначенню морфологічних особливостей їх зовнішнього огранювання).

Завдання:

1 Вивчити класифікацію простих форм і комбінацій за сингоніями та категоріями симетрії.

2 Згідно отриманого варіанту визначити: кристалографічну формулу моделей кристалу та встановити вид симетрії, сингонію і категорію симетрії.

3 За зовнішнім видом кристалів визначити: кристали (з однаковими по формі та розміру гранями), які називаються простими формами і кристали (які складені різними за форма­ми та розмірами гранями), що є комбінаціями простих форм.

4 Встановити їх назви та положення в класифікації симетрії.

1 Основні теоретичні положення

В ідеальних умовах „вільного росту” кристали утворюються у вигляді багатокутників з різною кількістю граней.

За зовнішнім виглядом кристали поділяються на дві групи: прості форми або комбінації простих форм.

Вивчення елементів симетрії не завжди дає повне уявлення про кристал. Часто абсолютно різні кристали за своїм зовнішнім виглядом відносяться до одного і того ж виду симетрії. При вивченні кристалічних багатогранників необхідно особливу увагу звернути на їх зовнішню форму, тобто на характер їх огранювання.

1.1 Простою формою називається сукупність однакових за зовнішньою формою і розмірами (в ідеальному вигляді) граней, пов’язаних між собою елементами симетрії, а також однаковими структурними і фізико-хімічними властивостями.

Серед простих форм виділяють відкриті (рис. 2.1, а) і закриті (рис. 2.1, б, в).

Відкриті прості форми характеризуються тим, що їх грані повністю не закривають простір (кристал) з усіх сторін; закриті - закривають простір повністю з усіх сторін.

а б в

Рисунок 2.1 - Приклад простих форм: а – відкрита, складена трьома прямокутними гранями; б – закрита, складена чотирма трикутними гранями; в – закрита, складена шістьома квадратними гранями.

Проста форма, грані якої розміщуються похило відносно всіх осей і площин симетрії, називається загальною. Проста форма, грані якої розміщуються перпендикулярно або паралельно відносно хоча б однієї осі і площини симетрії або рівно похилі до двох однакових елементів симетрії носить назву конкретної.

Для деяких простих форм, які характеризуються наявністю поворотних осей симетрії L₂, L₃, L₄, L₆ властиві явища енантіоморфізму, тобто наявності правих і лівих форм. Для цих простих форм характерно зміщення – закручення граней в праву і ліву сторони.

1.2 Вчення про прості форми кристалів і їх видів [1] дозволили встановити серед них найбільш характерні, які одержали назву характеристичних (табл. 2.1). Так, в трикліній сингонії виділено дві характеристичні прості форми (моноедр і пінакоїд), в моноклінній – три (дієдр осьовий, дієдр площинний і призма), в ромбічній – три (тетраедр, піраміда і біпіраміда), в тригональній – п’ять (піраміда, ромбоедр, трапецоедр, дітригональна піраміда і скаленоедр), в тетрагональній – сім (піраміда, біпіраміда, трапецоедр, дітетрагональна піраміда, де тетрагональна біпіраміда, тетраедр, скаленоедр), в гексагональній – сім (піраміда, біпіраміда, дігексагональна піраміда, дігексагональна біпіраміда і тригональна біпіраміда), в кубічній - п’ять (пентагонтритетраедр, дідодекаедр, пентагонтриоктаедр, гексатетраедр, гексаоктаедр).

Таблиця 2.1 - Характеристичні прості форми 32 видів симетрії

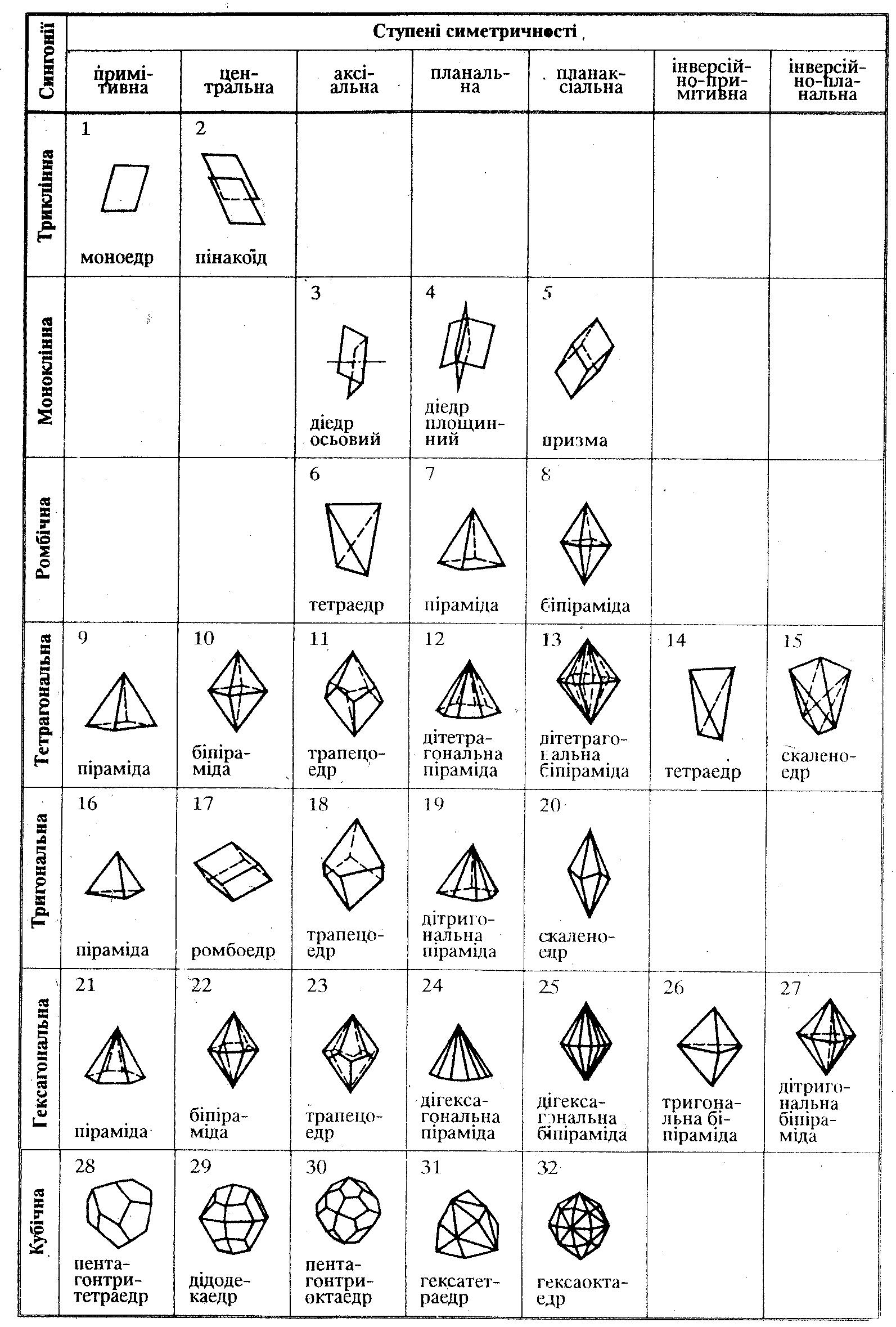
Як видно, до характерних простих форм належать прості форми з максимальним розвитком граней в кожній із семи ступенів симетричності (табл. 2.2, 1.3) [2].

Таблиця 2.2 - Назва 32 видів (класів) симетрії кристалів згідно характеристичних простих форм

Категорія	Сингонія	№	Назва виду симетрії згідно характеристичної простої форми (за Гротом)	Формула симетрії
Нижча	Триклинна	1	Моноедричний
		2	Пінакоїдальний	С
	Моноклінна	3	Діедрично-осьовий	L2
		4	Діедрично-планальний	Р
		5	Призматичний	С L2P
	Ромбічна	6	Ромбо-тетраедричний	3 L2
		7	Ромбо-пірамідальний	L22Р
		8	Ромбо-біпірамідальний	C3L23P
Середня	Тригональна	9	Тригонально- пірамідальний	L3
		10	Ромбоедричний	СL3
		11	Тригонально-трапецоедричний	L33L2
		12	Дітригонально-пірамідальний	L33P
		13	Дітригонально-скаленоедричний	СL33L23Р
	Тетрагональна	14	Тетрагонально-пірамідальний	L4
		15	Тетрагонально-біпірамідальний	CL4P
		16	Тетрагонально-трапецоедричний	L44L2
		17	Дітетрагонально-пірамідальний	L44P
		18	Дітетрагонально-біпірамідальний	CL44L25P
		19	Тетрагонально-тетраедричний	Li4 (L2)
		20	Тетрагонально-скаленоедричний	Li4 2L22Р
	Гексагональна	21	Гексагонально-пірамідальний	L6
		22	Гексагонально-біпірамідальний	L6 PC
Середня	Гексагональна	23	Гексагонально-трапецоедричний	L66L2
		24	Дігексагонально-пірамідальний	L66P
		25	Дігексагонально-біпірамідальний	СL66L27P
		26	Тригонально-біпірамідальний	L6і (L3P)
		27	Дітригонально-біпірамідальний	L6і3L23P (L33L24P)
Вища	Кубічна	28	Пентагонтритетраедричний	4L33L2
		29	Дідодекаедричний	С4L33L23Р
		30	Пентагонтриоктаедричний	4L33L26Р
		31	Гексатетраедричний	4L33L26P
		32	Гексаоктаедричний	C4L33L46L29P

Визначення простих форм кристалів рекомендується проводити таким чином:

а) суміщенням вихідної грані простої форми з аналогічною обертом її на певний кут навколо поворотної осі симетрії;

б) відбиттям вихідної грані простої форми з аналогічною через площину симетрії;

в) відбиттям – інверсією вихідної грані простої форми з аналогічною через центр інверсії;

г) суміщенням – інверсією вихідної грані простої форми з аналогічною поворотом навколо осі інверсій і наступним відбиттям через центр.

При визначенні простої форми на відповідних моделях необхідно пам’ятати, що вони подані в ідеальному вигляді, тобто відповідають математичній моделі кристалу. На реальних кристалах в більшості випадків зовнішня форма простих форм і їх відносні розміри не відповідають ідеальним моделям. В цих випадках при визначенні простих форм візуальним методом необхідно особливу увагу звернути на взаємо розміщення окремих граней і уявно пов’язати їх так, щоб в кінцевому підсумку уявити кристал в ідеальному вигляді.

1.3 Комбінація являє собою сукупність простих форм, пов’язаних між собою комплексом елементів симетрії (за винятком комбінацій примітивного виду триклинної сингонії, в якому елементи симетрії відсутні).

Серед комбінацій виділяють: прості, які складаються з одного виду простих форм, і складні, що складені різними простими формами (рис. 2.2).

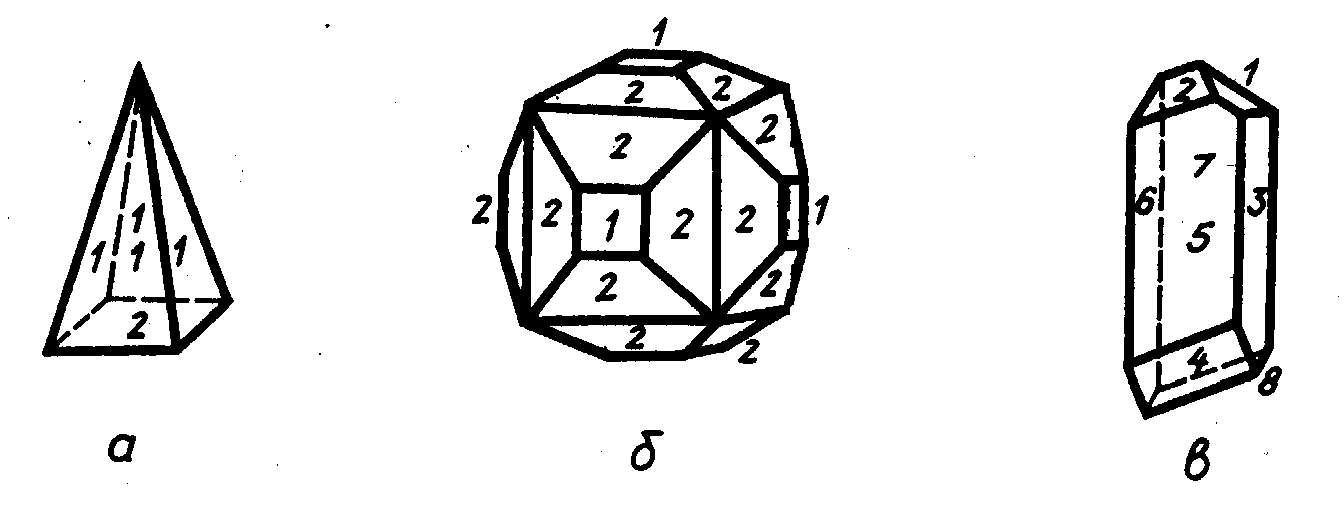
Рисунок. 2.2 - Приклади комбінацій: а - комбінація тетрагональної піраміди (1) і моноедра (2); б – комбінація куба (1) і тетрагексаедра (2); в – комбінація 8 – моноедрів (1, 2, 3, 4, 5, 6, 7, 8).

Кількість простих форм, що входять в цю чи іншу комбінацію, виводиться математично графічним шляхом і визначається формулою симетрії. При цьому кожному виду симетрії властива своя група простих форм, які утворюють комбінації (табл. 2.3). Так, в комбінації триклинної сингонії входять дві прості форми, моноклінної - чотири, ромбічної - сім, тригональної - одинадцять, гексагональної - дев’ять і кубічної - п’ятнадцять. Як видно, прості форми триклинної сингонії переходять в моноклінну, ромбічну, тригональну, тетрагональну і гексагональну сингонію. Для комбінацій кубічної сингонії властиві лише власні 15 простих форм, тобто прості форми з інших сингоній в кубічну не переходять, що вказує на її вищу симетрію.

При розшифруванні комбінацій рекомендується наступний порядок: 1 - визначення формули симетрії, 2 - визначення сингоній, 3 - визначення простих форм.

Операції, за допомогою яких ведеться розшифровка комбінацій, аналогічні тим, які проводяться при розшифровці простих форм.

Таблиця 2.3 - Перелік можливих з’єднань простих форм кристалів в комбінаціях 32 видів симетрії

Сингонія	Вид симетрії		Прості форми		Кількість простих форм
Триклінна	-		Моноедр		1
	С		Пінакоїд		1
Моноклінна	L2		Діедр; пінакоїд; моноедр		3
	Р		Діедр; пінакоїд; моноедр		3
	CL2P		Призма ромбічна; пінакоїд		2
Ромбічна	3L2		Тетраедр ромбічний; пінакоїд		3
	L22P		Тетраедр ромбічний; призма ромбічна; пінакоїд		5
	C3L23P		Піраміда ромбічна; призма ромбічна; діедр; пінакоїд; моноедр		3
Тригональна	L3		Піраміда тригональна; призма тригональна; Моноедр		3
	CL3		Призма гексагональна; ромбоедр; пінакоїд		3
	L33L2		Призма тетрагональна; призма гексагональна; призма дітригональна; біпіраміда тригональна; ромбоедр; трапецоедр тригональний		7
	L33P		Піраміда тригональна; піраміда дітригональна; пі­раміда гексагональна; призма тригональна; призма дітригональна; призма гексагональна; моноедр		7
	CL33L23Р		Призма гексагональна; призма дігексагональна; біпіраміда гексагональна; скаленоедр дітригональний; ромбоедр; пінакоїд		6
Тетрагональна	L4		Біпіраміда ромбічна; призма ромбічна; пінакоїд		3
	CL4P		Призма тетрагональна; біпіраміда тетрагональна; пінакоїд		3
	L44L2		Призма тетрагональна; призма дітетрагональна; біпіраміда тетрагональна; трапецоедр тетрагональна; пінакоїд		5
	L44P		Призма тетрагональна; призма дітетрагональна; піраміда тетрагональна; моноедр		5
	CL44L25P		Призма тетрагональна; призма дітетрагональна; біпіраміда тетрагональна; біпіраміда дітетрагональна; пінакоїд		5
	Li4(→L2)		Призма тетрагональна; тетраедр тетрагональний; пінакоїд		3
	Li42L22P		Призма тетрагональна; призма дітетрагональна; бі­піраміда тетрагональна; тетраедр тетрагональний; скаленоедр тетрагональний; пінакоїд		6
Продовження таблиці 2.3
Сингонія		Вид симетрії	Прості форми	Кількість простих форм
Гексагональна		L6	Призма гексагональна; піраміда гексагональна; моноедр	3
		CL6P	Призма гексагональна; піраміда дігексагональна; пінакоїд	3
		L66L2	Призма гексагональна; призма дігексагональна; біпіраміда гексагональна; трапецоедр гексагональний; пінакоїд	5
		L66P	Призма гексагональна; призма дігексагональна; піраміда гексагональна; піраміда дігексагональна; моноедр	5
		CL66L27P	Призма гексагональна; призма дігексагональна; біпіраміда гексагональна; піраміда дігексагональна; пінакоїд	5
		Li6 (= L3P)	Призма тригональна; біпіраміда тригональна; пінакоїд	3
		Li63L23P (= L33L24P)	Призма тригональна; призма гексагональна; призма дітригональна; біпіраміда тригональна; біпіраміда дітригональна; біпіраміда дігексагональна	7
Кубічна		L44L2	Тетраедр; гексаедр; ромбододекаедр; тригонтритетраедр; тетрагонтритетраедр; пентагонтритетраедр	7
		L44P	Гексаедр; октаедр; дідодекаедр; тригонтриоктаедр; тетрагонтриоктаедр; ромбододекаедр; пентагондодекаедр;	7
		CL44L25P	Гексаедр; октаедр; ромбододекаедр; тетрагексаедр; тригонтриоктаедр; пентагонтриоктаедр	7
		Li4 (= L2)	Тетраедр; гексаедр; ромбододекаедр; тетрагексаедр; тригонтритетраедр; тетрагонтритетраедр; гексатетраедр	7
		Li42L22P	Гексаедр; октаедр; ромбододекаедр; тетрагексаедр; тригонтриоктаедр; тетрагонтриоктаедр; гексаоктаедр	7

В процесі роботи з комбінаціями кристалів необхідно в першу чергу встановити методом простих підрахунків наявність всіх простих форм, грані яких характеризуються однаковою формою і розміром (в ідеальному вигляді). При цьому необхідно пам’ятати, що зовнішня форма граней окремих простих форм в комбінаціях з іншими простими формами значно відрізняється від зовнішньої форми граней окремих простих форм в ідеальному вигляді. Отже, при визначенні простих форм в комбінації необхідно в уяві продовжити всі наявні грані, що відносяться до цієї простої форми, до повного їх перетину та одержати уяву про комбінацію в ідеальному вигляді [1].