Лекция 7 Циклические коды Общие сведения

Циклические коды относятся к классу линейных систематиче­ских кодов и обладают всеми их свойствами.

Кодовые комбинации циклического кода удобно рассматри­вать не в виде последо­вательности нулей и единиц, а в виде полинома некоторой сте­пени.

Любое число в любой системе счисления можно предста­вить в общем виде как

где х — основание системы счисления;

а_i - цифры данной системы счисления;

n-1, n-2,... — показатель степени, в которую возво­дится основание системы счисления. Этот показатель степени совпадает с порядковым номером, который за­нимает разряд в кодовой комбинации (начиная от старшего разряда и кончая нулевым).

Для дво­ичной системы счисления х=2, а_i - либо «0», либо «1». Например, двоичную последовательность 01001 можно записать в виде полинома от ар­гумента х:

или, заменяя основание счисления 2 на x, получаем:

Очевидно, что при записи кодовой комбинации в виде много­члена единица в i-м разряде записывается членом х^i-1, а нуль во­обще не записывается. Представление кодовых комбинаций в виде многочленов позволяет установить однозначное соответствие между ними ­и свести действия над комбинациями к действию над многочленами.

Рассмотрим некоторые действия над двоичными многочленами:

1. Сложение двоичных многочленов сводится к сложению по модулю 2 коэффициентов при равных степенях переменной x. Например:

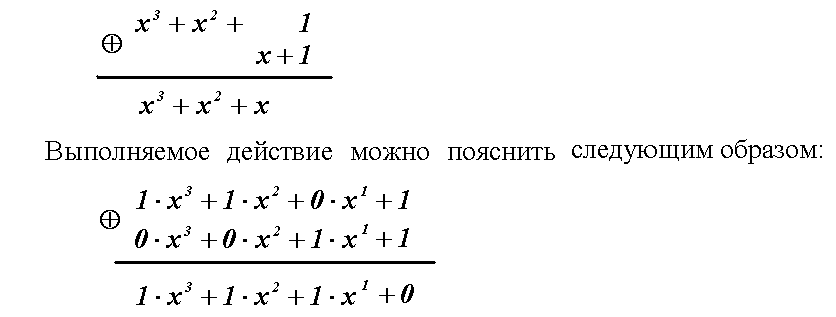
2. Умножение производится по обычному правилу умножения степенных функций, однако полученные коэффициенты при данной степени складываются по модулю 2. Например:

(x³+x²+0+1)(x+1)=x⁴+x³+0+x+x³+x²+0+1=x⁴+x²+x+1.

3. Деление также осуществляется, как обычное деление многочленов, при этом операция вычитания заменяется операцией сложе­ния по модулю 2 (сложение и вычитание двоичных чисел дают один и тот же результат: 1 1=0, 1 1=0). Например:

Данные коды называются циклическими потому, что циклический сдвиг разрешенной комбинации также является разрешенной комбинацией. Если кодовая комбинация представлена в виде полинома, то циклический сдвиг на 1 разряд эквивалентен умножению данного полинома на x.

Если

V(x)=a_n-1x^n-1+a_n-2x^n-2+…a₁x+a₀, то

V(x)·x=a_n-1xⁿ+a_n-2x^n-1+…+a₁x²+a₀x¹,

где V(x) – исходная кодовая комбинация,

V(x)·x – комбинация полученная из исходной при циклическом сдвиге на 1 разряд.

Чтобы степень многочлена не превышала n-1, член a_n-1xⁿ заменяется единицей, поэтому получаем:

V(x)·x=F(x)=a_n-2x^n-1+…+a₁x²+a₀x+a_n-1.

Пример

Пусть имеем кодовую комбинацию 0101110, которую представим в виде многочлена x⁵+x³+x²+x. Требуется произвести сдвиг данной комбинации на 1 разряд.

Получим 1011100 или многочлен вида x⁶+x⁴+x³+x².

Очевидно, что x⁶+x⁴+x³+x²=x·(x⁵+x³+x²+x).

Построение разрешенных комбинаций циклического кода

Всe разрешенные комбинации цикличе­ского кода, представленные в виде полиномов, обладают од­ним признаком: они делятся без остатка на образующий полином Р(х). Образующие полиномы P(x) относятся к классу неприводимых многочленов, т.к. они не могут быть представлены в виде произведения многочленов низших степеней. Неприводимый многочлен делится только на самого себя и на единицу.

Характерным для циклических кодов является то, что проверочная часть получается сразу, а не вычисляется отдельно для каждого разряда проверочной части.

Алгоритм построения разрешенной кодовой комбинации

1. Представляем информационную часть кодовой комбинации длиной k в виде полинома Q(x).

2. Умножаем Q(x) на одночлен х^r (r – число проверочных разрядов в кодовой комбинации) и получаем Q(x·)x^r, т. е. про­изводим сдвиг k-разрядной кодовой комбинации на r разрядов.

3. Делим многочлен Q(x)·x^r на образующий полином Р(х), сте­пень которого равна r (т.е. степень образующего полинома совпадает с числом проверочных разрядов).

Результаты этих операций можно представить в виде

где C(x) – целая часть полученная при делении Q(x)·x^r на образующий полином Р(х),

R(x) - остаток от деления Q(x)·x^r на Р(х).

Умножим обе части полученного выражения на Р(х), получим

или

(знак вычитания в выражении заменяется знаком сложения по модулю 2). Оче­видно, что F(x) делится на Р(х) без остатка. Полином F(x) пред­ставляет собой разрешенную кодовую комбинацию циклического кода.

Из полученного выражения следует, что разрешенную кодовую комбинацию цик­лического кода можно получить двумя способами:

1. Умножить кодовую комбинацию простого кода С(х) на образующий полином Р(х) (для этого вначале требуется найти C(x) – это целая часть полученная при делении Q(x)·x^r на образующий полином Р(х)).

2. Умножить кодовую комбинацию Q(x) простого кода (т.е. заданную информационную комбинацию) на одночлен х^r и прибавить к этому произведению (сложение провести по модулю 2) остаток R(x), полученный в результате деления произведения Q(x)·x^r на образующий полином Р(х).

Пример

Дана кодовая комбинация 0111. Построить циклический код с расстоянием Хэмминга d₀=3.

Исходя из требуемого расстояния Хэмминга d₀=3, определим количество проверочных элементов r, равное показателю степени образующего полинома. Воспользуемся формулой Так как число информационных элементов известно (k=4), то, учитывая, что n=k+r, имеем Отсюда r=3. Следовательно, необходимо сформировать код (7,4).

По таблице образующих полиномов (см. далее) при r=3 находим P(x)=x³+x+1.

Далее действуем по описанному алгоритму:

1. Записываем информационную часть заданной кодовой комбинации длиной k в виде полинома Q(x)= x²+x+1.

2. Умножаем Q(x) на x³ (так как r=3):

2. Делим Q(x)·x³ на P(x):

Получаем x²+x и x в остатке. Следовательно, R(x)=x и C(x)= x²+x.

2. Находим разрешенную комбинацию циклического кода (7,4) по 2-му способу:

Этот полином соответствует кодовой комбинации

Пример

Доказать, что кодовая комбинация полученная в предыдущем примере является разрешенной.

Для проверки разделим полученный многочлен F(x) на образующий полином P(x):

Полином F(x) делится на P(x) без остатка, следовательно, кодовая комбинация является разрешенной.

Пример

Для заданной кодовой комбинации 0111 построить разрешенную кодовую комбинацию кода (7,4) первым способом.

В предыдущих примерах получено:

C(x)= x²+x и P(x)=x³+x+1.

Согласно первому способу разрешенная комбинация циклического кода равна:

Подставляя, получаем:

Полином соответствует двоичной комбинации 0111010.

Таблица образующих полиномов циклического кода

r	Pr(x)	Двоичная запись многочлена P(x)
2	x2+x+1	111
3	x3+x+1	1011
4	x4+x+1	10011
5	x5+x2+1 x5+x4+x3+x2+1 x5+x4+x2+x+1	100101 111101 110111
6	x6+x+1 x6+x5+x2+x+1	1000011 1100111
7	x7+x3+1 x7+x3+x2+x+1 x7+x4+x3+x2+1	10001001 10001111 10011101
8	x8+x7+x6+x5+x2+x+1 x8+x4+x3+x2+1 x8+x6+x5+x+1	111100111 100011101 101100011
9	x9+x5+x3+x2+1 x9+x8+x7+x6+x5+x3+1	1000101101 1111101001
10	x10+x4+x3+x+1 x10+x9+x6+x5+x4+x3+x2+x+1	10000011011 11001111111
11	x11+x10+x9+x8+x3+x+1 x11+x8+x6+x2+1	111100001011 100101000101
12	x12+x11+x9+x8+x7+x5+x2+x+1 x12+x9+x3+x2+1	1101110100111 1001000001101