Индивидуальное задание №4

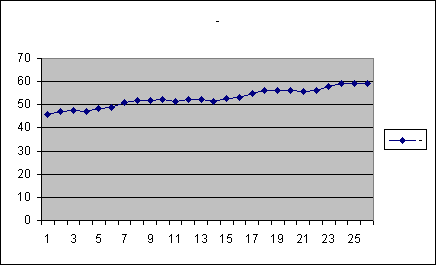
Задан динамический ряд числа проданных телевизоров

Месяц	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24
Продажа	46	56	54	43	57	56	67	62	50	56	47	56	54	42	64	60	70	66	57	55	53	62	70	72

Требуется:

1. провести предварительный анализ данных;

2. с помощью функций - кандидатов провести формирование набора моделей;

1. найти численные значения параметров моделей на основании метода наименьших квадратов;

2. определить адекватность моделей

3. оценить точность адекватных моделей;

4. выбрать наилучшую модель;

5. получить точечный и интервальный прогнозы на следующие два месяца;

6. провести верификацию полученных прогнозов.

Решение.

1. Проведем сглаживание заданного динамического ряда с помощью метода экспоненциального сглаживания, приняв величину сглаживания =0,1. Построим полученную сглаженную линию регрессии.

месяц	продажа	Сглаж. Значение
1	46	-							0,1
2	56	46
3	54	47
4	43	47,7
5	57	47,23
6	56	48,207
7	67	48,9863
8	62	50,78767
9	50	51,9089
10	56	51,71801
11	47	52,14621
12	56	51,63159
13	54	52,06843
14	42	52,26159
15	64	51,23543
16	60	52,51189
17	70	53,2607
18	66	54,93463
19	57	56,04117
20	55	56,13705
21	53	56,02334
22	62	55,72101
23	70	56,34891
24	72	57,71402
25	57,71402	59,14262

Из графика видно, что временной ряд экономического показателя имеет тренд, т.е. преобладающую тенденцию изменения. Предполагая, что общие условия, определявшие развитие показателя в прошлом, останутся без существенных изменений в течение периода упреждения, найдем кривые роста, для моделирования и прогнозирования продаж телевизоров.

2. В качестве тренда для заданного временного ряда можно принять следующие модели: а) линейную модель

;

б) экспоненциальную модель

в) логарифмическую модель

.

Для заданного временного ряда уравнения трендов имеют соответственно вид:

а) линейная модель

;

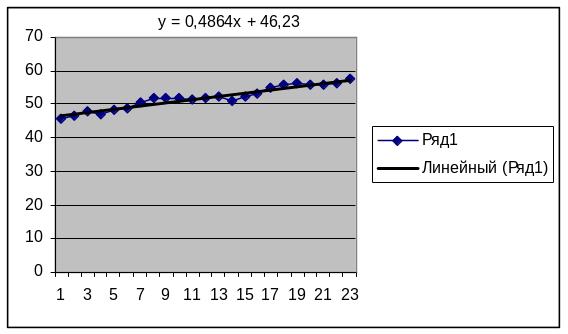
Предположение о линейности тренда подтверждают рассчитанные первые приросты или цепные приращения, которые являются практически постоянными величинами.

б) экспоненциальную модель

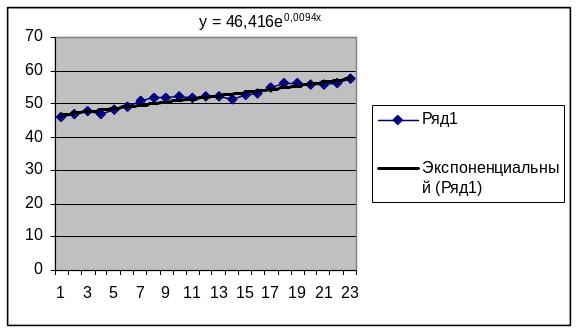
в) логарифмическую модель

.

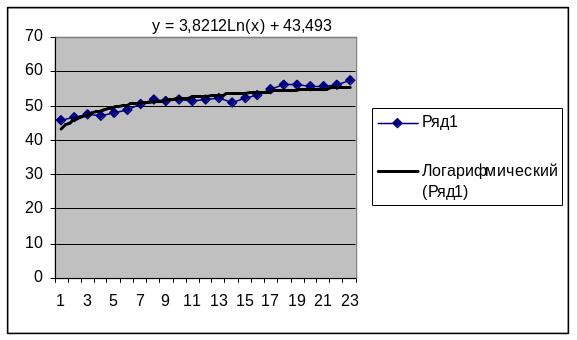
3. Численные значения параметров модели можно рассчитать на основании метода наименьших квадратов. Для этого рассматриваемую модель нужно свести к линейной, а затем, решая систему нормальных уравнений, определить неизвестные коэффициенты.

4. Оценим точность полученной трендовой модели.

Линейная модель

t	Фактическое	Расчетное	Отклонение	Точки пиков
1	2	3	4	5	6	7	8	9
1	42	46,716	-4,716	-	22,244	-		11,230
2	54	47,203	6,797	1	46,202	11,514	132,563	12,587
3	57	47,689	9,311	1	86,691	2,514	6,318	16,335
4	40	48,176	-8,176	1	66,840	-17,486	305,774	20,439
5	59	48,662	10,338	1	106,87	18,514	342,753	17,522
6	56	49,148	6,852	1	46,944	-3,486	12,155	12,235
7	67	49,635	17,365	1	301,55	10,514	110,536	25,918
8	62	50,121	11,879	0	141,106	-5,486	30,101	19,159
9	50	50,608	-0,608	1	0,369	-12,486	155,910	1,215
10	56	51,094	4,906	1	24,069	5,514	30,400	8,761
11	47	51,580	-4,580	1	20,980	-9,486	89,992	9,746
12	56	52,067	3,933	1	15,470	8,514	72,481	7,024
13	54	52,553	1,447	0	2,093	-2,486	6,182	2,679
14	42	53,040	-11,040	1	121,873	-12,486	155,910	26,285
15	64	53,526	10,474	1	109,705	21,514	462,835	16,366
16	60	54,012	5,988	1	35,851	-4,486	20,128	9,979
17	70	54,499	15,501	1	240,287	9,514	90,509	22,145
18	66	54,985	11,015	0	121,326	-4,486	20,128	16,689
19	57	55,472	1,528	0	2,336	-9,486	89,992	2,681
20	55	55,958	-0,958	0	0,918	-2,486	6,182	1,742
21	53	56,444	-3,444	1	11,864	-2,486	6,182	6,499
22	62	56,931	5,069	0	25,697	8,514	72,481	8,176
23	70	57,417	12,583	0	158,327	7,514	56,454	17,975
24	72	57,904	14,096	-	198,708	1,514	2,291	19,578
300	1371	1255,440	115,560	15	1908,32		2278,257	312,965

Для этого всего сформируем остаточную последовательность (ряд остатков), для чего из фактических значений уровней ря­да вычтем соответствующие расчетные значения по модели: остаточная последовательность приведена в гр. 4 таблицы.

Проверку случайности уровней ряда остатков проведем на основе критерия пиков (поворотных точек).

Уровень последова­тельности считается максимумом, если он больше двух рядом стоящих уровней, т.е.

,

и минимумом, если он меньше обоих соседних уровней, т.е.

.

Точки максимума и минимума последовательности называются поворотными точками.

Общее чис­ло поворотных точек для остаточной последовательности обозначим через .

В случайной выборке математическое ожидание числа точек поворота и дисперсия выражаются формулами:

,

Критерием случайности с 5%-ным уровнем значимости, т.е. с доверительной вероятностью 95%, является выполнение неравенства

,

где квадратные скобки означают целую часть числа. Если это неравенство не выполняется, трендовая мо­дель считается неадекватной.

Точки пиков от­мечены в гр. 5 таблицы; их количество равно = 15. Находим для заданного случая математическое ожидание числа точек поворота и дисперсию

, .

Для рассматриваемой модели выполняется неравенство

.

Вывод: с доверительной вероятностью 95%, можно утверждать, что линейная трендовая мо­дель является адекватной, т.к. свойство случайности ряда остат­ков подтверждается.

Проверка соответствия распределения случайной ком­поненты нормальному закону распределения. Для этого воспользуемся -критерием, в основе которого критерия лежит исследование отношения размаха вариа­ции случайной величины к стандартному отклонению . Эти величины определяются следующим образом

, .

Вычисленное значение критерия сравнивается с табличными (критическими) нижней и верхней границами данного отношения, и если это значение не попадает в интервал между критическими границами, то с заданным уровнем значимости гипотеза о нормальности распределения отвергается; в про­тивном случае эта гипотеза принимается. Для иллюстрации приведем несколько пар значений критических границ -критерия для уровня значимости = 0,05.

10	2,67	3,685
20	3,18	4,49
30	3,47	4,89

В нашем случае размах вариации

=

а среднее квадратическое отклонение

= .

Сравнивая значение = с табличными (критическими) значениями нижней и верхней границ данного отношения, видим, что значение попадает в интервал между нижней и верхней границами табличных значений данного критерия. Эти границы для = 20 и уровня значимости = 0,05 составляют соответственно 3,18 и 4,49. Это позволяет сделать следующий вывод.

Вывод: свойство нормальности распреде­ления выполняется.

в) Проверка равенства математического ожидания слу­чайной компоненты нулю, если она распределена по нор­мальному закону, осуществляется на основе -критерия Стьюдента.

Расчетное значение этого критерия задается формулой

,

где — среднее арифметическое значение уровней остаточ­ной последовательности ;

— стандартное (среднеквадратическое) отклонение для этой последовательности.

Если расчетное значение меньше табличного значения статистики Стьюдента с заданным уровнем значимости и числом степеней свободы , то гипотеза о равенстве нулю математического ожидания случайной последовательности принимается; в противном случае эта гипотеза отвергается и модель считается неадекватной.

Переходя к проверке равенства (близости) нулю матема­тического ожидания ряда остатков для рассматриваемой модели, находим по результатам вычислений, приведенных в таблице,

= ,

= 7,505287,

=3,142929.

Вывод: Т.к. расчетное значение =3,142929 меньше табличного значения статистики Стьюдента с заданным уровнем значимости = 0,05 и числом степеней свободы = 24-1=23, то гипотеза о равенстве нулю математического ожидания случайной последовательности принимается.

г) Проверка независимости значений уровней случайной компоненты, т.е. проверка отсутствия существенной авто­корреляции в остаточной последовательности может осуще­ствляться по ряду критериев, наиболее распространенным из которых является d-критерий Дарбина—Уотсона.

Рас­четное значение этого критерия определяется по формуле

.

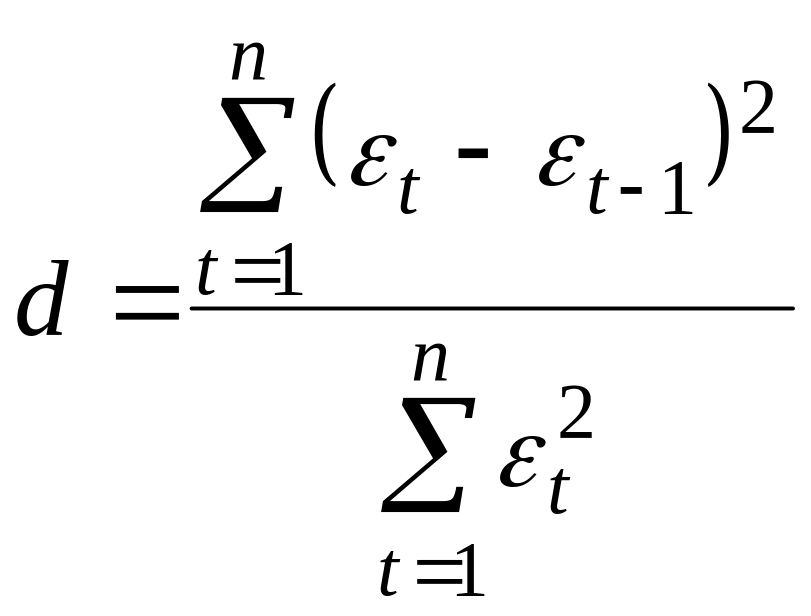Заметим, что расчетное значение критерия Дарбина-Уотсона в интервале от 2 до 4 свидетельствует об отрицательной связи; в этом случае его надо преобразовать по формуле и в дальнейшем использовать значение .

Расчетное значение критерия (или ) сравнивается с верхним и нижним критическими значениями ста­тистики Дарбина—Уотсона, фрагмент табличных значений которых для различного числа уровней ряда и числа опре­деляемых параметров модели представлен в табл. (уровень значимости 5%).

15	1,08	1,36	0,95	1,54	0,82	1,75
20	1,20	1,41	1,10	1,54	1,00	1,68
30	1,35	1,49	1,28	1,57	1,21	1,65

Если расчетное значение критерия больше верхнего табличного значения , то гипотеза о независимости уров­ней остаточной последовательности, т.е. об отсутствии в ней автокорреляции, принимается. Если значение меньше нижнего табличного значения , то эта гипотеза отвергается и модель неадекватна. Если значение находится между значениями и включая сами эти значения, то считается, что нет достаточных оснований сделать тот или иной вывод и необходимы дальнейшие исследования, например, по боль­шему числу наблюдений.

Для рассматриваемой модели находим

=1,193852.

Т.к. найденное значение удовлетворяет неравенству , то это свидетельствует об отрицательной связи; в этом случае его надо преобразовать по формуле

и в дальнейшем использовать значение . Расчетное значение критерия сравниваем с верхним и нижним критическими значениями ста­тистики Дарбина—Уотсона, фрагмент табличных значений которых для различного числа уровней ряда и числа опре­деляемых параметров модели представлен в табл. (уровень значимости 5%).

Вывод об адекватности трендовой модели делается, если все указанные выше четыре проверки свойств остаточной последовательности дают положительный результат.