32.Ряд Тейлора (Маклорена)
1. Если
,
то коэффициент
разложения
данной функции в ряд Маклорена равен…
Ответ: -10
2. Разложение в ряд по степеням
функции
имеет
вид
Ответ:
3. Ряд Маклорена для функции
имеет
вид
Ответ:
1/3
4. Если
,
то первые три (отличные от нуля) члена
разложения этой функции в ряд Маклорена
имеют вид
Ответ:
5. Ряд Маклорена для функции
имеет
вид
Ответ:
6. Если
,
то коэффициент
разложения
данной функции в ряд Тейлора по степеням
равен…
Ответ: 9
7. Ряд Маклорена для функции
имеет
вид
Ответ:
8. Разложение в ряд Тейлора функции
в
окрестности точки
имеет
вид
Ответ:
9. Если
,
то коэффициент
разложения
данной функции в ряд Тейлора по степеням
равен…Ответ:
0
10. Если
,
то первые три (отличные от нуля) члена
разложения этой функции в ряд Маклорена
имеют вид… Ответ:
33. Системы линейных уравнений
1. Система
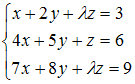совместна,
если
равно
… Ответ: 1
2. Базисное решение системы
может
иметь вид …
Ответ:
3. Однородная система
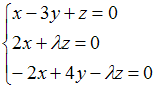имеет
только одно нулевое решение, если
принимает
значения не равные … Ответ: 2
4. Для невырожденной квадратной матрицы
решение
системы
в
матричной форме имеет вид …
Ответ:
5. Метод Гаусса для решения систем линейных уравнений заключается …
Ответ: в последовательном исключении переменных
6. Решение системы линейных уравнений
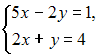методом
Крамера может иметь вид
Ответ:
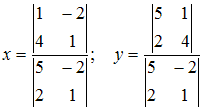
7. Система
не
имеет решений, если
равно
…Ответ: – 2
8. Единственное решение имеет однородная система линейных уравнений …
Ответ:
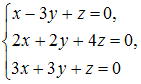
9. Однородная система имеет только одно нулевое решение, если принимает значения не равные … Ответ: 2
34 Скалярное произведение векторов
1) В ортонормированном базисе заданы
векторы
и
.
Тогда их скалярное произведение будет
равно …
Ответ: 13
2) Даны два вектора:
и
,
где
,
,
угол между векторами
и
равен
.
Тогда скалярное
произведение векторов
и
будет
равно …
Ответ: – 3
3) Даны точки
и
.
Тогда скалярное произведение
радиус-векторов этих точек равно …
Ответ: 5
4) Векторы
и
взаимно
перпендикулярны, если значение параметра
равно …
Ответ: -7
5) В ортонормированном базисе заданы
векторы
и
.
Тогда их скалярное произведение будет
равно
при
равном …
Ответ: 3
6) Дан вектор
,
где
,
,
угол между векторами
и
равен
.
Тогда модуль вектора
будет
равен …
Ответ: 
7) Даны два вектора:
и
,
где
,
,
угол между векторами
и
равен
.
Тогда скалярное
произведение векторов
и
будет
равно …
Ответ: 4
8) В ортонормированном базисе заданы
вектора
и
.
Эти векторы будут взаимно перпендикулярны,
если значение параметра
равно …
Ответ: -3
9) Скалярное
произведение векторов
и
равно …
Ответ: -3
10) Угол между векторами
и
,
заданными в ортонормированном базисе,
равен …
Ответ: