
- •1. Асимптоты графика функции
- •2. Вычисление определителей
- •3. Градиент скалярного поля
- •7. Равен нулевому вектору в точке …
- •8. В точке равен …
- •10. Модуль градиента скалярного поля в точке равен …
- •4. Дифференциалы и теоремы о дифференцируемых функциях
- •6. Дифференциал функции равен …
- •5. Дифференциальное исчисление фнп
- •Частная производная второго порядка функции имеет вид …
- •Частная производная функции имеет вид …
- •6.Дифференциальные уравнения высших порядков, допускающие понижение порядка
- •7. Дифференциальные уравнения с разделяющимися переменными
- •8. Дифференцирование функции комплексного переменного
- •7) Значение производной функции в точке равно …
- •10) Значение производной функции в точке равно …
- •9. Задача Коши для дифференциального уравнения первого порядка
- •10. Квадратичные формы.
- •29. Производные первого порядка
- •30. Прямая на плоскости.
- •31. Прямоугольные координаты на плоскости
- •32.Ряд Тейлора (Маклорена)
- •33. Системы линейных уравнений
- •34 Скалярное произведение векторов
- •35. Смешанное произведение векторов
- •36 Сходимость числовых рядов
10. Квадратичные формы.
Матрице
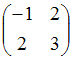 соответствует
квадратичная форма
соответствует
квадратичная форма
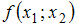 ,
равная …
,
равная …

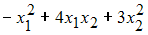
Положительно определенная квадратичная форма может иметь вид …

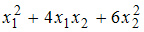
Матрица квадратичной формы
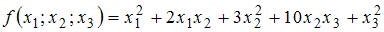 имеет
вид …
имеет
вид …
Канонический вид квадратичной формы
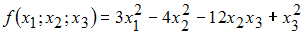 может
иметь вид …
может
иметь вид …
Отрицательно определенная квадратичная форма может иметь вид …
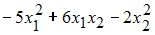
Канонический вид квадратичной формы
 может
иметь вид …
может
иметь вид …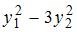
Матрице
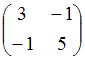 соответствует
квадратичная форма
равная …
соответствует
квадратичная форма
равная …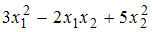
Матрица квадратичной формы
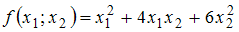 имеет
вид …
имеет
вид …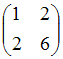
Матрице
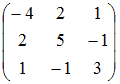 соответствует
квадратичная форма
соответствует
квадратичная форма
![]() ,
равная …
,
равная …
|
|
|
|
Квадратичная форма, не являющаяся знакоопределенной, может иметь вид …
|
|
|
|
11.Линейные операции над матрицами 1.
Дана матрица
Ответ:
2.
Даны матрицы
Ответ:
3.
Матрицы
Ответ:
4.
Даны матрицы
Ответ:
5.
Даны матрицы
Ответ:
6.
Дана матрица
Ответ:
7.
Даны матрицы
Ответ: 2
8.
Даны матрицы
Ответ: 85
12. Норма вектора в евклидовом пространстве 1.
Скалярное произведение векторов
Ответ: 4 2. Скалярное произведение векторов и равно 5, угол между векторами равен , норма вектора равна 2. Тогда норма вектора равна … Ответ:5 3.
Если
Ответ:5 4.
Даны векторы
Ответ:3 5.
Даны векторы
и
Ответ:
6.
Норма вектора
Ответ:6 7.
Норма вектора
Ответ:3 8.
Даны векторы
и
,
угол между которыми равен
.
Проекция вектора
на
вектор
равна
Ответ:6 9.
Если
и
–
ортогональные векторы из евклидова
пространства со стандартным скалярным
произведением, такие что
Ответ: 10 10.
Норма вектора
Ответ: -2 13 Области на комплексной плоскости 1)Все
точки
2)Все точки
комплексной
плоскости, принадлежащие множеству
,
изображенному на рисунке:
3) Все точки
комплексной
плоскости, принадлежащие множеству
,
изображенному на рисунке,
4) Все точки
комплексной
плоскости, принадлежащие множеству
,
изображенному на рисунке:
5) Все точки
комплексной
плоскости, принадлежащие множеству
,
изображенному на рисунке:
6) Все точки
комплексной
плоскости, принадлежащие множеству
,
изображенному на рисунке,
7) Все точки
комплексной
плоскости, принадлежащие множеству
,
изображенному на рисунке,
8) Все точки
комплексной
плоскости, принадлежащие множеству
,
изображенному на рисунке:
9) Все точки
комплексной
плоскости, принадлежащие множеству
,
изображенному на рисунке:
10) Все точки
комплексной
плоскости, принадлежащие множеству
,
изображенному на рисунке,
14. Область определения функции
1. Область
определения функции
Ответ:
2. Область
определения функции
Ответ: 0,5
3. Область
определения функции
Ответ:
4. Область
определения функции
Ответ: 5
5. Область
определения функции
Ответ:
6. Область
определения функции
Ответ:
7. Область
определения функции
Ответ:
8. Область
определения функции
Ответ:
9. Область определения вида
Ответ:
10. Область
определения функции
Ответ:
Ответ:
16. Обратная матрица
1. Обратной для матрицы
2. Для матрицы
3. Если
Ответ:
4. Для матрицы
Ответ: 2
5. Для матрицы
6. Для матрицы
существует
обратная, если ее определитель…
Ответ:
7. Обратной для матрицы
8. Для матрицы
9. Обратной для матрицы является матрица… Ответ:
10. Для матрицы
17. Операторный метод решения дифференциальных уравнений
Ответ:
Ответ:
Ответ:
Ответ:
Ответ:
Ответ:
Ответ
Ответ:
Ответ:
18. Операторный метод решения систем дифференциальных уравнений
Ответ:
Ответ:
Ответ
19.Операции над комплексными числами
3. Сумма комплексных чисел
4. Если
Ответ:
5.
Если
6. Частное
7. Произведение комплексных чисел
и
равно…Ответ:
8. Если
и
–
корни квадратного уравнения
Ответ:
9. Частное от деления
10. Произведение комплексных чисел
и
20. Определение линейного пространства
1. Среди представленных множеств линейное пространство образует …
Ответ: множество всех векторов,
принадлежащих пространству
2. Аксиомой линейного пространства
Ответ:
3. Среди представленных множеств линейное пространство не образует … Ответ: множество всех матриц размерностью m´n, содержащих только положительные числа
4. Линейное пространство не обладает свойством …
Ответ: для любого
5. Операции сложения
и умножения на действительное число
линейного пространства обладают
свойством … Ответ:
6. На линейном пространстве задана операция …
Ответ:
7. Среди представленных множеств линейное пространство образует … Ответ: множество всех комплексных чисел
8. На линейном пространстве задана операция …
Ответ:
9. Аксиомой линейного пространства является …
Ответ:
10. Линейное пространство обладает следующим свойством:
Ответ:
21. Определение функции комплексного переменного
1) Если
и
2) Дана функция
3) Если
Ответ:
4) Если
и
–
комплексно-сопряженные числа, то
действительная часть функции
5) Если
6) Если
и
–
комплексно-сопряженные числа, то
действительная часть функции
7) Если
8) Дана функция
9) Если
Ответ:
22 Оригинал изображения
1.Если
функция
2.
Оригинал
Ответ:
3.
Если функция
Ответ:
4.
Если функция
Ответ:
5.
Если функция
6.
Если функция
является
изображением оригинала
,
то оригиналом изображения
7.
Если функция
8. Если функция является изображением, то оригинал имеет вид … Ответ:
9.
Если функция
Ответ:
23. Основные методы интегрирования
|
|
|
|
7. Объем тела, полученного вращением
вокруг оси
![]() криволинейной
трапеции, ограниченной параболой
криволинейной
трапеции, ограниченной параболой
![]() и
осью
,
равен …
и
осью
,
равен …
Ответ: ![]()
8. Площадь фигуры, ограниченной параболой
![]() и
осью
,
равна … Ответ: 36
и
осью
,
равна … Ответ: 36
9. Объем тела, полученного вращением
вокруг оси
криволинейной
трапеции, ограниченной параболой
![]() и
осью
,
равен …
и
осью
,
равен …
Ответ:
![]()
10. Длина дуги кривой
![]() от
точки
от
точки
![]() до
точки
до
точки
![]() равна
…
равна
…
Ответ: ![]()
1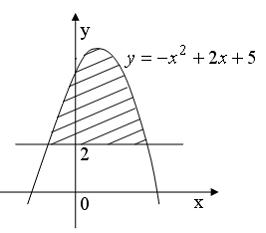 1.
Площадь фигуры, изображенной на рисунке
равна … Ответ:
1.
Площадь фигуры, изображенной на рисунке
равна … Ответ:

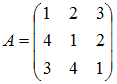 .
Если матрица
.
Если матрица
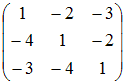
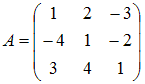 и
и
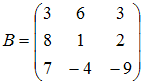 .
Тогда решением уравнения
.
Тогда решением уравнения
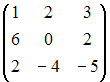

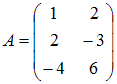 ,
,
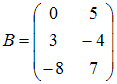 .
Тогда матрица
.
Тогда матрица
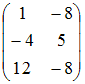
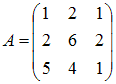 .
Тогда матрица
.
Тогда матрица
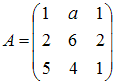 и
и
 и
и
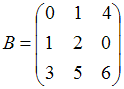 .
Если
.
Если
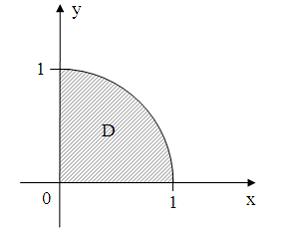 удовлетворяют
условию …
удовлетворяют
условию …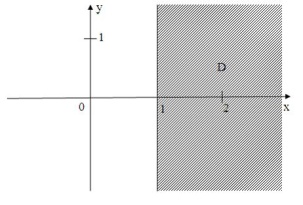 удовлетворяют
условию …
удовлетворяют
условию …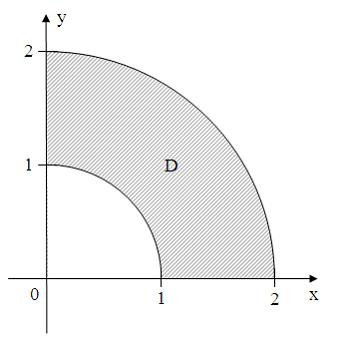 удовлетворяют
условию …
удовлетворяют
условию …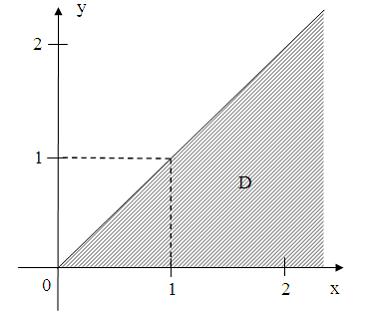 удовлетворяют
условию …
удовлетворяют
условию …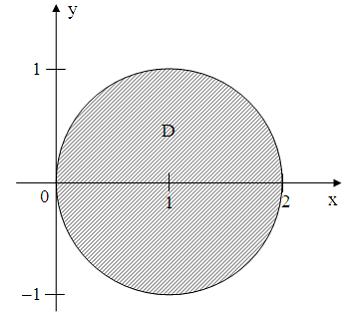 удовлетворяют
условию …
удовлетворяют
условию …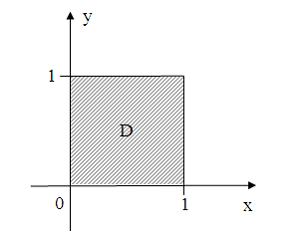 удовлетворяют
условию …
удовлетворяют
условию …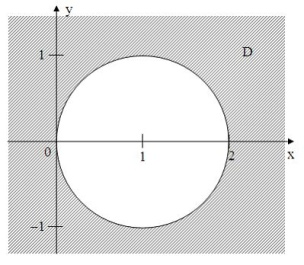 удовлетворяют
условию …
удовлетворяют
условию …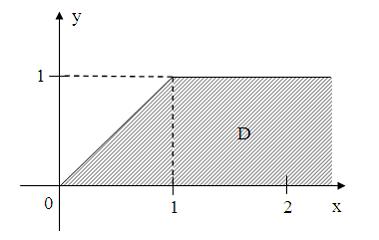 удовлетворяют
условию …
удовлетворяют
условию …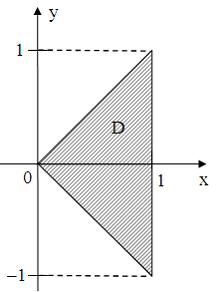 удовлетворяют
условию …
удовлетворяют
условию …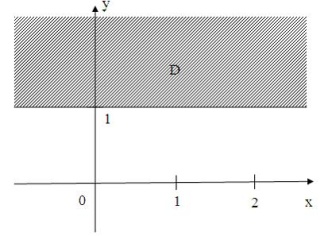 удовлетворяют
условию …
удовлетворяют
условию …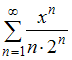 имеет вид … Ответ:
имеет вид … Ответ:
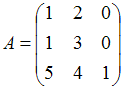 обратная
матрица равна… Ответ:
обратная
матрица равна… Ответ:
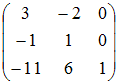
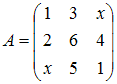 не
существует обратной, если значение
не
существует обратной, если значение
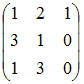
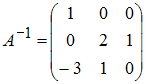 является
матрица… Ответ:
является
матрица… Ответ:
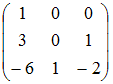
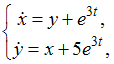 при
при
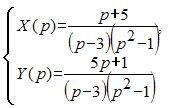
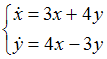 при
при
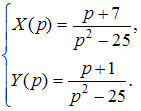
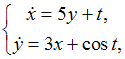 при
имеет
вид …Ответ:
при
имеет
вид …Ответ:
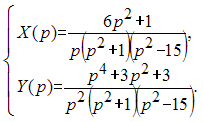
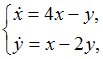 при
при
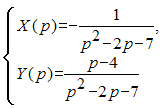
 при
при
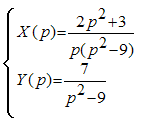
 при
имеет
вид … Ответ:
при
имеет
вид … Ответ:
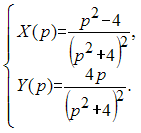
 при
при
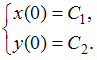 Тогда
соответствующая система операторных
уравнений имеет вид …
Тогда
соответствующая система операторных
уравнений имеет вид …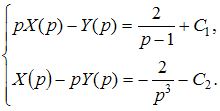
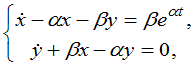 при
при
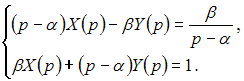
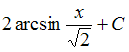
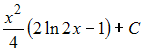
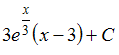
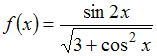 имеет
вид …
имеет
вид …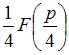
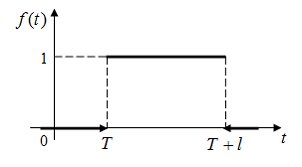

 имеет
вид …Ответ:
имеет
вид …Ответ:
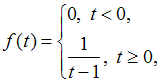 В)
В)
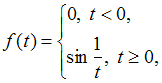 С)
С)
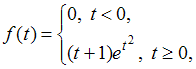 D)
D)
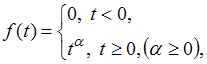 оригиналом
является …
оригиналом
является …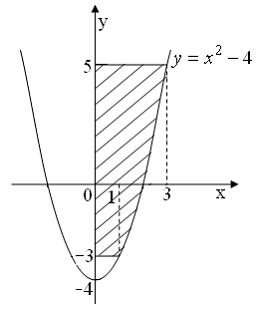 .
Площадь фигуры, изображенной на
рисунке
равна … Ответ:
.
Площадь фигуры, изображенной на
рисунке
равна … Ответ:
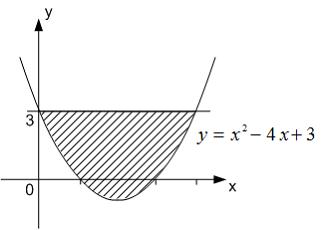
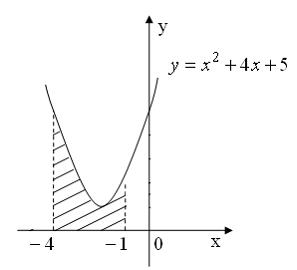 .
Площадь фигуры, изображенной на
рисунке
равна … Ответ: 6
.
Площадь фигуры, изображенной на
рисунке
равна … Ответ: 6 .
Площадь фигуры, изображенной на
рисунке
равна … Ответ:
.
Площадь фигуры, изображенной на
рисунке
равна … Ответ:
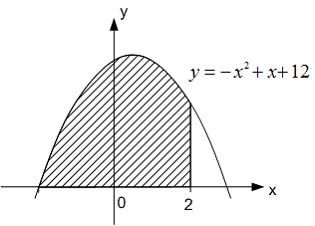 .
Площадь фигуры, изображенной на
рисунке
равна … Ответ:
.
Площадь фигуры, изображенной на
рисунке
равна … Ответ: