
- •Кафедра общей и технической физики Лаборатория физики твердого тела и квантовой физики Лабораторная работа 10
- •1. Основные теоретические сведения.
- •1.1. Контакт двух металлов
- •1.2. Термоэлектрические эффекты
- •2. Экспериментальная часть
- •2.1. Типы термопар
- •2.2. Экспериментальная установка.
- •2.3. Порядок выполнения работы
- •1. Градуировка термопары
- •2. Измерение неизвестной температуры.
- •3. Обработка результатов измерений
- •4. Контрольные вопросы.
2. Экспериментальная часть
2.1. Типы термопар
Термоэлектрические свойства материалов принято характеризовать величиной термо-ЭДС, развиваемой этими материалами в паре с чистой платиной при температуре рабочего конца термопары 100 и свободного конца 0 ºС. В табл.1. приведены термо-ЭДС развиваемые различными материалами в указанных условиях.
Табл.1.
Металл или сплав |
Химический состав |
Термо-ЭДС, мэВ |
Хромель |
89Ni+9.8Cr+1Fe+0.2 Mn |
+2.9 |
Железо |
Fe |
+1.8 |
Медь |
Cu |
0.76 |
Платинородий |
90Pt+10Rn |
0.64 |
Платина |
Pt |
0.00 |
Алюмель |
94Ni+2Al+2.5Mn+1Si+0.5Fe |
-1.2 |
Константан |
60Cu+40Ni |
-3.5 |
Копель |
56Cu+44Ni |
-3.9 |
Знак + в графе термо-ЭДС показывает, что данный электрод в паре с платиной является положительным электродом, т.е. что в горячем спае условное направление тока - от платины к данному электроду. Термо-ЭДС пары из любых двух термоэлектродов определяется по таблице как алгебраическая разность их термо-ЭДС с платиной. Положительным термоэлектродом пары будет тот электрод, чья термо-ЭДС в паре с платиной относительно больше.
Многие неметаллические материалы (графит, карборунд) и полупроводники могут быть использованы в качестве термоэлектродов, причем образованные из них термопары способны создавать термо-ЭДС в сотни раз больше, чем у металлических термопар. Однако полупроводниковые и смешанные термопары не получили пока широкого применения для технических измерений температуры главным образом из-за большого разброса термоэлектрических характеристик, приводящего к необходимости индивидуальной градуировки каждого экземпляра термопар. В настоящее время наибольшее применение для технических измерений имеют следующие стандартные термопары (ГОСТ 6616-53).
Термопара платинородий -платина (условное обозначение ПП). Эта термопара применяется для технических измерений температур выше 1000 ºС, а также в качестве эталонных, образцовых и лабораторных приборов. Верхний предел измерения термопары (1500 ºС при длительном нагреве) определяется главным образом прочностью платинового электрода.
Термопара хромель-алюмель (условное обозначение ХА), пределы измерения от -50 до +1000 ºС, а при кратковременном нагреве до 1300 ºС.
Термопара хромель-копель (условное обозначение ХК), пределы измерения от -50 до +600 ºС, а при кратковременном нагреве до 800 ºС.
Для измерения температуры жидкой стали в плавильных печах в пределах 1400-1800 ºС применяются термопары графит-молибден. Эти термопары невзаимозаменяемые, и каждая из них градуируется при выпуске.
В диапазоне температур от -200 до +400 ºС находит применение термопара медь-константан.
2.2. Экспериментальная установка.
Экспериментальная установка представлена на рис.3 и состоит из стеклянного стакана 1, в который наливается вода, термометра 2, усилителя напряжения 3, мультиметра 4 и термопары 5.
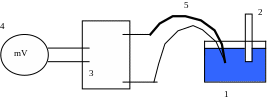
Рис.3.Схема установки
Электродвижущую силу термопары можно измерять вольтметром, если его внутреннее сопротивление достаточно велико по сравнению внутренним сопротивлением термопары. Составим электрическую цепь из термопары (с ЭДС Е и внутренним сопротивлением r) и вольтметра, внутреннее сопротивление которого RV. Сопротивление подводящих проводов R. По закону Ома
E=Ir+IR+IRV, (11)
где
UV=IRV (12)
- падение напряжения на внутреннем сопротивлении вольтметра.
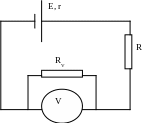
Рис.4. Эквивалентная схема.
При измерении ЭДС термопара вольтметром подразумевается , что UV=E, т.е допускается систематическая ошибка ΔE=I(R+r), что в процентном отношении к измеряемой величине Е составляет
![]() (13)
(13)
Сопротивление ветвей термопары r и сопротивление подводящих проводов R - малы (~10-2 Ом). При внутреннем сопротивлении вольтметра RV=109 Ом систематическая ошибка оказывается незначительной : δ=(10-2/109) 100%=10-9 %.
