Графы. Модели вычислений. Структуры данных

где αij, βi – регулярные выражения, Xi – переменные (i, j = 1, 2, …, n). Решением системы называется набор (L(X1), L(X2), …, L(Xn)) фор-

мальных языков, которые при подстановке вместо соответствующих переменных в уравнения обращают их в равенства. Удобно на решение смотреть как на отображение L, которое каждой переменной Xi ставит в соответствие язык L(Xi). Решение L1 называется наименьшей неподвижной точкой системы, если для любого другого решения L выполняются соотношения L1(Xi) L(Xi) при i = 1, 2, …, n.

Теорема. Каждая стандартная система уравнений имеет единственную неподвижную точку.

Доказательство. Действительно, нетрудно видеть, что отображение L1, определяемое по формуламL1 (X i ) = IL(X i ) , где пересечение берет-

L

ся по всем решениям L (i = 1, 2, …, n), является искомой неподвижной точкой системы.

Решаются такие системы уравнений методом исключения неизвестных. Если, например, α11 ≠ , то первое уравнение можно представить в

виде X1 = α11X1 + β, где β = α12 X2 + … +α1n Xn + β1, записать его решение описанным выше способом в виде (α11)*β и подставить в остальные уравнения. Получим систему с меньшим числом неизвестных и так далее.

5.5. Автоматное задание языков

Недетерминированные конечные автоматы с ε-переходами. Неде-

терминированным конечным автоматом с ε-переходами над алфавитом A называется набор

= (Q, A, q0, F, ϕ),

где Q – множество состояний, A – алфавит, q0 – начальное состояние (q0Q), F – множество финальных состояний (F Q), ϕ: Q × (A {ε}) → 2Q

– переходная функция.

Такой автомат можно представить нагруженным ориентированным мультиграфом (диаграммой) следующим образом. Вершинами графа объявить состояния, то есть элементы множества Q, и если q′ ϕ(q, x), то из

151

состояния q в состояние q′ провести дугу, помеченную символом x

(A {ε}).

Язык L( ), порождаемый автоматом , состоит из всех слов, которые можно прочитать, двигаясь, начиная со стартового состояния q0, по ребрам и читая приписанные им символы. Чтение заканчивается в любом из финальных состояний множества F не обязательно при первом туда попадании. При чтении символов воспринимать ε как пустое слово.

Пример 2 . Пусть алфавит A = {a, b, c}, Q = {q0, q1, q2}, F = {q1} и переходная функция ϕ задана таблицей

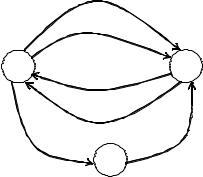
Диаграмма автомата изображена на рис. 1.

Рис. 1

Недетерминированные конечные автоматы без ε-переходов. Неде-

терминированным конечным автоматом без ε-переходов над алфавитом A называется набор

= (Q, A, q0, F, ϕ),

где Q – множество состояний, A – алфавит, q0 – начальное состояние

(q0 Q), F – множество финальных состояний (F Q) и ϕ: Q × A → 2Q – переходная функция. Такой автомат также можно представить нагружен-

ным ориентированным мультиграфом (диаграммой). Отличие в том, что дуги могут быть помечены только символами алфавита A.

152

Язык L( ), порождаемый таким автоматом , состоит из всех слов, которые можно прочитать, двигаясь, начиная со стартового состояния q0, по ребрам и читая приписанные им символы. Чтение заканчивается в любом из финальных состояний множества F не обязательно при первом туда попадании.

Детерминированные конечные автоматы. Детерминированным ко-

нечным автоматом над алфавитом A называется набор

= (Q, A, q0, F, ϕ),

где Q – множество состояний, A – алфавит, q0 – начальное состояние

(q0 Q), F – множество финальных состояний (F Q) и ϕ: Q × A → Q – переходная функция. Такой автомат также можно представить нагружен-

ным ориентированным мультиграфом (диаграммой). Отличие от недетерминированного автомата в том, что из каждого состояния выходит ровно одна дуга, помеченная конкретной буквой алфавита A, причем для каждой буквы алфавита такая дуга существует.

Язык L( ), порождаемый таким автоматом , определяется аналогично тому, как это было для недетерминированных автоматов.

Теорема. Классы языков, задаваемые регулярными выражениями, недетерминированными конечными автоматами с ε-переходами, недетерминированными конечными автоматами без ε-переходов, детерминированными конечными автоматами, совпадают.

Доказательство. Для доказательства достаточно по каждому регулярному выражению научиться строить равносильный недетерминированный конечный автомат с ε-переходами (синтез), затем избавляться от ε-переходов, затем детерминизировать и, наконец, по детерминированному автомату строить регулярное выражение (анализ).

Синтез. Регулярное выражение представляется автоматом =

= (Q, A, q0, F, ϕ), где Q = {q0, q1}, алфавит A – произволен, q0 – начальное состояние, F = {q1} – множество финальных состояний и переходная функ-

ция ϕ задается соотношениями ( x A {ε}) ϕ(q0, x) = , ϕ(q1, x) = . Регулярное выражение λ представляется автоматом = (Q, A, q0, F, ϕ), где Q = {q0, q1}, алфавит A – произволен, q0 – начальное состояние, F = {q1} – множество финальных состояний и переходная функция ϕ за-

дается соотношениями ϕ (q0, ε) = {q1}, ϕ(q1, ε) = и ( x A) ϕ (q0, x) = ,

ϕ (q1, x) = .

Регулярное выражение a (a A) представляется автоматом = (Q, A,

153

q0, F, ϕ), где Q = {q0, q1}, q0 – начальное состояние, F = {q1} – множество финальных состояний и переходная функция ϕ задается соотношениями

ϕ(q0, a) = {q1}, ( x (A {ε}) \ {a}) ϕ (q0, x) = и ( x (A {ε}))

ϕ(q1, x) = .

Для регулярного выражения (P S), где P и S – регулярные выражения, можно построить задающий автомат = (Q, A, q0, F, ϕ) следующим

образом. Пусть автомат 1 = (Q1, A, q1, F1, ϕ1) задает L (P), а автомат2 = (Q2, A, q2, F2, ϕ2) задает L(S). Не уменьшая общности, можно считать, что F1 = {f1} и F2 = {f2} – одноэлементные и что q1 ≠ f1 , q2 ≠ f2. Положим Q = Q1 Q2 {q0, f }, где q0, f – новые состояния, и поясним по-

строение автомата на языке диаграмм. Состояние q0 соединим дугами со стартовыми состояниями q1, q2 автоматов 1, 2 и пометим их символом ε. Состояния f1 и f2 автоматов 1, 2 соединим дугами с новым состоянием f и также пометим их символом ε. Начальным состоянием построенного автомата объявим q0, а финальным – f.

Для регулярного выражения P S, где P и S – регулярные выражения, можно построить задающий автомат = (Q, A, q0, F, ϕ) следующим об-

разом. Пусть автомат 1 = (Q1, A, q1, F1, ϕ1) задает L(P), а автомат2 = (Q2, A, q2, F2, ϕ2) задает L(S). Не уменьшая общности, опять счита-

ем, что F1 = {f1} и F2 = {f2} – одноэлементные и что q1 ≠ f1 , q2 ≠ f2. Положим Q = Q1 Q2 и поясним построение автомата на языке диаграмм.

Финальное состояние автомата 1 соединим дугой со стартовым состоянием автомата 2 и пометим ее символом ε. В качестве q0 возьмем стартовое состояние автомата 1, а в качестве финального состояния f возьмем финальное состояние f2 автомата 2.

Для регулярного выражения P*, где P – регулярное выражение, мож-

но построить задающий автомат new = (Q, A, q0, {f0}, ϕ) следующим образом. Пусть автомат 1 = (Q1, A, q1, {f1}, ϕ1) задает L(P). Опять не уменьшая общности, считаем, что F1 = {f1} – одноэлементное и что q1 ≠ f1.

Добавляем к множеству Q1 два новых состояния – q0 и f0. Соединяем ε-

переходами пары состояний (q0, q1), (f1, f0), (q0, f0) и (f1, q1).

В завершение заметим, что изложенные приемы очевидно позволяют по любому регулярному выражению R построить недетерминированный автомат с ε-переходами, с одним стартовым и одним финальным состоянием, причем стартовое состояние отлично от финального, и при этом такой, что L(R) = L( ).

154

Таким образом, задача синтеза решена.

Избавление от ε-переходов. Покажем, как по недетерминированному автомату = (Q, A, q0, F, ϕ) с ε-переходами построить недетерминиро-

ванный автомат 1 = (Q, A, q0, F1, ϕ1) без ε-переходов, такой, что L( 1) = = L( ). Назовем ε-путем путь в диаграмме автомата , возможно пустой,

порождающий пустое слово. Обозначим через λ(q) множество состояний, достижимых из q с помощью некоторого ε-пути.

Положим F1 = {q| существует ε-путь из q в F}. Переходную функцию ϕ1 построим следующим образом

ϕ1 (q, a) = Uϕ(q1, a) ,

q1λ(q)

Заметим, что в полученном автомате множество финальных состояний может быть не одноэлементным.

Детерминизация. Покажем, как по недетерминированному автомату

= (Q, A, q0, F, ϕ) без ε-переходов построить детерминированный автомат 1 = (Q1, A, q1, F1, ϕ1), такой, что L( 1) = L( ). Положим Q1 = 2Q, q1 = {q0}, F1= {q| (q Q) & (q ∩ F ≠ )}, а ϕ1: Q1 × A → Q1 определим следующим образом

( q Q1 )( a A)ϕ1 (q, a) = Uϕ(s, a) .

s q

Нетрудно видеть, что построенный таким образом автомат 1 удовле-

творяет условию L( 1) = L( ).

Анализ. Для завершения доказательства теоремы покажем, как по заданному детерминированному конечному автомату построить регулярное выражение R, такое, что L(R) = L( ). Именно это и называют задачей анализа. Правда, метод, который мы используем, можно применить и к недетерминированным автоматам. Метод заключается в том, что мы сводим задачу к решению стандартной системы уравнений. Итак, рассмот-

рим автомат = (Q, A, q0, F, ϕ).

Пусть Q = {q0, q1, …, qn}, A = {a1, a2, …, am}. Введем переменные X(q0), X(q1), …, X(qn). Переменную X(qi) для каждого i = 0, 1, …, n будем интерпретировать как множество слов, которые можно прочитать, начиная от состояния qi и заканчивая в финальном состоянии, тогда X(qi) должна удовлетворять уравнению

X(qi) = a1 X(ϕ(qi, a1)) + a2 X(ϕ(qi, a2)) + …+ am X(ϕ(qi, am)) + βi ,

155

где βi = λ, если qi F, βi = , если qi F. Решив систему, берем в качестве ответа значение переменной X(q0).

Задача. Построить регулярное выражение, задающее язык, порож-

даемый автоматом = (Q, A, q0, F, ϕ), где Q = {q0, q1, q2, q3}, A = {a, b},

F = {q3} и функция ϕ задана таблицей

Рис. 2

Решение. Запишем систему уравнений

X0 = aX3 + bX1, X1 = a X3 + bX2, X2 = aX2 + bX3,

X3 = aX1 + bX3 + λ.

Заметим, что при записи системы мы упростили обозначения переменных используя индексы.

Из четвертого уравнения получаем X3 = b*(aX1+λ). Подставляя полученное выражение во все остальные уравнения, получим систему из трех уравнений

X0 = a b*(aX1 + λ) + bX1, X1 = ab*(aX1 + λ) + bX2, X2 = aX2 + bb*(aX1 + λ).

156

Перепишем ее в стандартном виде

X0 = (ab*a + b)X1+ ab*, X1 = ab*aX1 + bX2 + ab*, X2 = bb*a X1 + aX2 + bb*.

Из третьего уравнения получаем X2 = a*(bb* aX1 + bb*) и подставляем в остальные уравнения

X0 = (ab*a + b) X1 + ab*,

X1 = ab*aX1 + ba*(bb*aX1 + bb*) + ab*.

Преобразуем второе уравнение к стандартному виду

X1= (ab*a + ba*bb*a) X1 + ba*bb* + ab*

и получаем из него

X1 = (ab*a + ba*bb*a)*(ba*bb* + ab*).

Наконец, получаем ответ

X0 = (ab*a + b)(ab*a + ba*bb*a)*(ba*bb* + ab*) + ab*.

5.6. Применение конечных автоматов в программировании

Задача. По заданному регулярному выражению α над алфавитом A = {a1, a2, …, an} найти в тексте x наименьший префикс, содержащий слово из L(α).

Решение. Строится регулярное выражение β = (a1 a2 … an)* α и для него – недетерминированный конечный автомат с ε-переходами. Пусть это будет автомат = (Q, A, q0, F, ϕ). Если при чтении текста x построенным автоматом мы приходим в финальное состояние, то это означает, что мы прочитали префикс текста x, содержащий слово из языка

L(α).

Алгоритм, моделирующий работу недетерминированного конечного автомата с ε-переходами на входном слове x = x1x2…xn A*

157

Q0:= {q0};

for i := 1 to n do Qi:= Uϕ(q, xi ) ;

q Qi−1

Пометить все состояния из Qi как рассмотренные; Пометить все состояния из Q \ Qi как нерассмотренные; Все состояния из Qi поместить в очередь;

While Очередь не пуста do

{t := головной элемент из очереди (с удалением); For u ϕ(t, ε) & u – не рассмотрен do

{Пометить u как рассмотренное; Поместить u в хвост очереди и в Qi}}

Оценим трудоемкость приведенного алгоритма. Пусть |Q| = m, |ϕ(q, a)| ≤ e, тогда тело цикла «while» оценивается как O(e), а тело цикла «for i := 1 to n do» как O(em) и весь алгоритм имеет трудоемкость O(e m n).

Анализируя алгоритм построения автомата = (Q, A, q0, {f }, ϕ) с ε-переходами по регулярному выражению β, легко установить следующие свойства:

•|Q|<2 |β|, где |β| – длина выражения β с учетом скобок и символов операций;

•q0 ≠ f ;

•( x (A {ε})) ϕ(f, x) = ;

• ( q Q) ∑|ϕ(q, x) |≤ 2 .

a ( A {ε})

Учитывая приведенные свойства, можем теперь оценить алгоритм, моделирующий работу автомата , величиной O(n |β|).

Рассмотрим теперь задачу частную по отношению к рассмотренной выше, полагая, что вместо регулярного выражения α, задано одно словообразец y.

Задача. Требуется найти вхождение заданного слова-образца y = = y1 y2 … yn в слово-текст x = x1 x2 … xm или установить, что такого вхождения нет.

Определение. По данному образцу y определим функцию Sy: A*→ A* следующим образом: ( x A*) Sy(x) – наибольший префикс слова y, являющийся суффиксом слова x.

Очевидно, ( x A*) Sy(x) = max{k prefk y = suffk x}.

Утверждение 1. Для любой строки x и любого символа a Sy(xa) ≤

158

≤ Sy (x) + 1.

Sy(xa) = Sy(y1 y2 … yqa) .

Действительно, по предыдущему утверждению, Sy (xa) ≤ q + 1, поэтому значение Sy (xa) не изменится, если от строки xa оставить последние q + 1 символов, а именно y1 y2 … yq a.

Построим по слову-образцу y = y1 y2 … yn конечный автомат = = (Q, A, q0, {f }, ϕ), где Q = {0, 1, …, n}, q0 = 0, f = n, а переходную функ-

цию ϕ определим следующим образом ( q Q)( a A) ϕ (q, a) = = Sy(y1 y2 … yqa) . Для построенного автомата, очевидно, будет справедливо следующее утверждение.

Утверждение 3. Прочитав текст x, автомат = (Q, A, q0, {f }, ϕ) будет находиться в состоянии Sy(x) .

Алгоритм вычисления функции переходов:

n := length(y);

for q:= 0 to n do for a A do k := min{n + 1, q + 2}; repeat k := k – 1 until y1y2…yq = suff (y1 y2 … yq a); ϕ (q, a) := k

Время работы этого алгоритма O(n3 A ).

Пример. Пусть алфавит A = {a, b} и Y = aabbaab. Допустим, что, читая текст x, мы обнаружили некоторый префикс x1x2…xi слова x, заканчивающийся фрагментом aabbaa, являющимся префиксом слова Y, а следующий символ xi+1 в тексте x не равен b, то есть не совпадает с очередным символом слова Y. Считаем, что потерпели неудачу, но при этом заметим, что суффикс aa этого фрагмента является его префиксом и, возможно, он является префиксом некоторого вхождения слова Y в x. Делая такое предположение, продолжаем читать x, сравнивая очередные символы слова x с соответствующими, начиная с третьего символами, слова Y в надежде на этот раз обнаружить его вхождение в x.

Таким образом, читая x, будем считать, что мы в каждый момент находимся в некотором состоянии j, если только что прочитан префикс Y ′ слова Y длины j. Если при чтении следующего символа терпим неудачу,

159

то переходим в новое состояние j ′, такое, что j ′ – максимальный префикс слова Y ′, являющийся его суффиксом. Функцию, которая состоянию j ставит в соответствие j ′, называют функцией откатов. В нашем примере ее можно изобразить следующей диаграммой.

Рис. 3

Введем необходимые обозначения. Пусть Y – непустое слово в некотором алфавите, а L(Y) – наибольший собственный префикс слова Y, являющийся его суффиксом. Тогда справедливы следующие утверждения:

1.Слова L2(Y), L3(Y), … являются собственными префиксами и суффиксами слова Y.

2.Последовательность L(Y), L2(Y), L3(Y), … обрывается на пустом

слове.

3.Любое префикс слова Y, являющийся его суффиксом, находится в последовательности L(Y), L2 (Y), L3 (Y), …

Пример. Пусть Y = abbabbabbacabbab. Тогда L (Y) = abbab,

L2 (Y) = ab,

L3 (Y) = λ.

Определение. Функцией откатов для слова Y = Y1Y2…Yn называют функцию f : {1, 2, …, n}→{0, 1, 2, …, n – 1}, определяемую соотношением f (i) = | L(pref iY ) |, где pref iY − префикс длины i слова Y.

В нашем примере функция f (i) задается следующей таблицей

Алгоритм Кнута − Морриса − Пратта построения функции откатов для слова Y = Y1 Y2 … Yn :

f (1) := 0;

160