Пункт 10.4. Дифференциальная форма теоремы о циркуляции магнитного поля.
10.4.1 Ротор («вихрь») векторного поля.
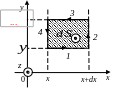
Рассмотрим
элементарный плоский контур в виде
прямоугольника, лежащего в плоскости
XY
в магнитном поле
(вообще говоря, неоднородном). Найдем
элементарную циркуляцию
поля
по этому контуру.
Совершаем обход против часовой стрелки.
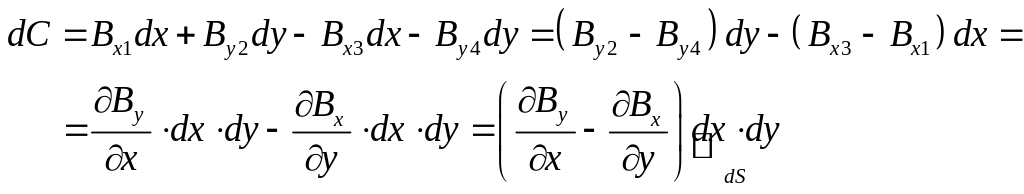
Рассмотрим отношение
циркуляции к площади
Для аналогичных контуров в плоскостях ZY и ZX, получим
Эта формула не зависит от формы контура.
Рассмотрим произвольную площадку контура, наклоненного к осям x,y,z. Удобен фрагмент плоскости в виде треугольника, стороны которого параллельны соответствующим координатным плоскостям.
Н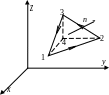
а
этом треугольнике построим тетраэдр с
гранями, параллельными координатным
плоскостям.
Введем по определению ротор поля .
(6).
(7)
Проекция ротора
поля
на
любое направление
равна
отношению циркуляции вектора поля
по
бесконечно малому контуру, перпендикулярному
,
к площади
,
охватываемой этим контуром.
Направление
совпадает
с направлением нормали к такой площадке,
для которой
максимально.
Используя оператор
Гамильтона
,
запишем
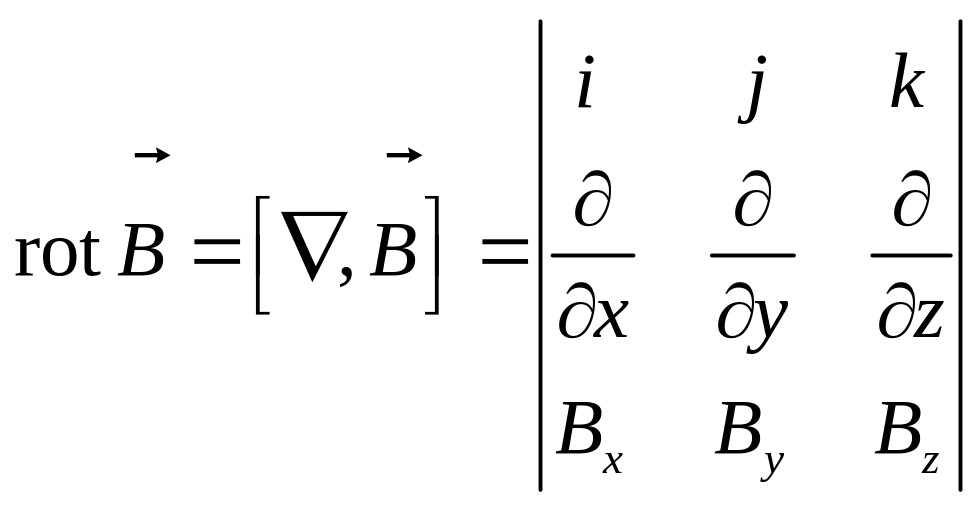(8)
Заметим, что (7) не зависит от системы координат, а (6) и (8) применимы только в декартовой.
Векторное поле,
ротор которого равен 0, называется
безвихревым, а если
,
то вихревым.
10.4.2 Локальная форма теоремы о циркуляции магнитного поля.
Воспроизведем
формулу
- теорема о циркуляции в интегральной
форме.
С учетом
-
связь между плотностью тока и величиной
тока.
Если мы подставим (5) в (3) и запишем полученное выражение для элементарного контура, то
Учтем здесь формулу (7).
,
т.к.
-
любой, то
.
(9) – локальная
форма теоремы о циркуляции магнитного
поля;
Очевидно, что магнитное поле будет вихревым только там, где плотность тока не равна нулю.