10. Основные законы стационарного (постоянного) магнитного поля.

10.1. Соленоидальность («трубкообразность») магнитного поля.

Непосредственным вычислением (чем мы заниматься не будем) можно показать, что дивергенция поля

, созданного точечным зарядом Q, движущимся со скоростью , равна нулю.

Таким образом, в рассматриваемом поле нет особенностей, аналогичных источникам или стокам («отрицательный заряд») электростатического поля, т.е. электрических зарядов.

Магнитные линии в отличие от силовых линий электростатического поля оказываются замкнутыми (однако, можно привести примеры, где они не являются замкнутыми  Смотри лекцию 7 Магнитное поле начало). Такое поле, (где магнитные линии замкнуты) называют бездивергентным или соленоидальным, т.е. «трубчатым».

В интегральной форме условие соленоидальности имеет вид:

.

Принцип суперпозиции для поля приводит к аддитивности потоков полей , создаваемых отдельными источниками.

Учет аддитивности Ф расширяет область применимости формулы . Более того, опыт показывает, что формулы и справедливы для любых магнитных полей, независимо от их происхождения.

10.2. Циркуляция магнитного поля постоянных токов.

Найдем циркуляцию магнитного поля по контуру Г: , созданного бесконечным прямолинейным проводником, т.е. лентой с током I. В пункте 8.6 (смотри пример 1) было показано, что это поле описывается формулой:

Выберем контур Г в виде окружности, совпадающей с одной из линий поля , а направление обхода совпадает с направлением линий поля, тогда

Формула справедлива для контура любой формы, а не только для окружности, плоскость которой перпендикулярна линиям тока.

Теперь возьмем произвольное направление и представим его в виде трех перемещений: , и так, как это показано на рисунке. Ясно, что любое перемещение в пространстве можно представить как суперпозицию этих трех взаимно перпендикулярных направлений.

Т .к. , ведь поле в нашем примере будет направлено по касательной к окружности, то

Остальные два слагаемых будет обращаться в ноль из-за перпендикулярности соответствующих векторов. Именно эта скобка имеется в виду в формуле .

Мы расширили области применимости формулы на произвольный замкнутый контур, охватывающий наш прямолинейный ток.

Формула справедлива и для случая, когда источником поля служат множество прямолинейных проводников с током.

(4)

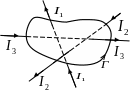
Теперь поговорим о том, что есть алгебраическая сумма токов. Выберем произвольный контур Г с некоторым направлением обхода, и произвольную поверхность, опирающуюся на этот контур, пронизывают рассматриваемые нами токи. В правой части формулы записана алгебраическая сумма токов, при этом для нашего примера (см. Рис) , знак токов определяется по правилу правого винта. В случае непрерывного распределения токов в пространстве можно записать:

(5)

- поток вектора через произвольную поверхность , опирающуюся на контур Г.

Рассмотренный пример показывает, что теорема о циркуляции вектора магнитной индукции может быть использована для расчета магнитных полей, создаваемых симметричным распределением токов, когда из соображений симметрии можно «угадать» общую структуру поля.

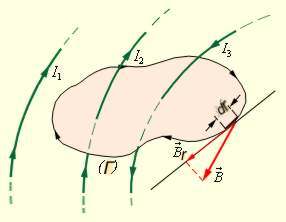
Рисунок 1

Замкнутый контур (L) с заданным направлением обхода. Изображены токи I₁, I₂ и I₃, создающие магнитное поле

В качестве примера на рис. 1. изображены несколько проводников с токами, создающими магнитное поле. Токи I₂ и I₃ пронизывают контур L в противоположных направлениях, им должны быть приписаны разные знаки – положительными считаются токи, которые связаны с выбранным направлением обхода контура правилом правого винта (буравчика). Следовательно, I₃ > 0, а I₂ < 0. Ток I₁ не пронизывает контур L.

Теорема о циркуляции в данном примере выражается соотношением