14.5 Векторный и комплексный методы описания гармонических колебаний

Пусть вектор (с модулем а) вращается вокруг своего начала - точки О в плоскости ХОY - с постоянной угловой скоростью (рис. 10) против часовой стрелки. При этом проекция вектора на ось Х зависит от времени по гармоническому закону:

x(t) =  a cos ( ).

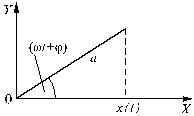
Рис. 10. Вращающийся вектор и его проекция на ось Х, колеблющаяся по гармоническому закону

Такое свойство проекции равномерно вращающегося вектора положено в основу так называемого метода векторных диаграмм. Метод удобен, например, для выполнения операции сложения двух колебаний:

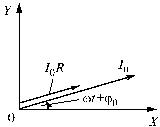
Примем во внимание еще одно важное свойство: проекция суммарного вектора равна сумме проекций каждого из слагаемых векторов и . На рис. 11 показано взаимное расположение всех трех векторов: , , , а также ось Х в момент t = 0. Благодаря одинаковой угловой скорости вращения векторов и угол между ними изменяться не будет. Это означает, что и вектор , величина которого постоянна, вращается с той же угловой скоростью. Таким образом, треугольник векторов вращается, не деформируясь, с угловой скоростью .

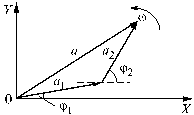
Рис. 11. Иллюстрация к сложению двух гармонических колебаний методом векторных диаграмм

Возвращаясь к рассмотрению колебаний, находим

x = x₁ + x₂ = a cos ( ),

где

Для наглядного решения уравнения вынужденных колебаний можно использовать метод векторных диаграмм.

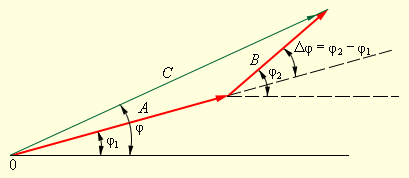
На векторной диаграмме колебания определенной заданной частоты ω изображаются с помощью векторов (рис. 2.3.2).

Рисунок 2.3.2. Изображение гармонических колебаний A cos (ωt + φ1), B cos (ωt + φ2) и их суммы C cos (ωt + φ) с помощью векторов на векторной диаграмме

Длины векторов на диаграмме равны амплитудам A и B колебаний, а наклон к горизонтальной оси определяется фазами колебаний φ₁ и φ₂. Взаимная ориентация векторов определяется относительным фазовым сдвигом Δφ = φ₁ – φ₂. Вектор, изображающий суммарное колебание, строится на векторной диаграмме по правилу сложения векторов:

Для того, чтобы построить векторную диаграмму напряжений и токов при вынужденных колебаниях в электрической цепи, нужно знать соотношения между амплитудами токов и напряжений и фазовый сдвиг между ними для всех участков цепи.

Второй метод описания гармонических колебаний связан с понятием комплексных чисел и называется методом комплексных амплитуд. Он опирается на знаменитую формулу Эйлера:

,

которая тригонометрическим функциям действительного аргумента ставит в соответствие показательную функцию с комплексным показателем степени.

Таким образом, комплексная функция

 (22)

имеет действительную часть, совпадающую с традиционным уравнением гармонических колебаний:

x(t) = Rez(t) = a cos ( ).

Введем понятие комплексной амплитуды

. (23)

С учетом определения (23) комплексная форма записи уравнения гармонических колебаний (22) принимает вид

.

Заметим, что комплексность амплитуды свидетельствует о ненулевом значении начальной фазы .

Применим метод комплексных амплитуд и метод векторных диаграмм к выяснению амплитудных и фазовых соотношений между напряжением и током для основных элементов электрической цепи: индуктивности, емкости, сопротивления и генератора гармонического напряжения.

Индуктивность. Гармонический ток

I(t) = I₀ cos ( ),

текущий через индуктивность, представим как действительную часть комплексной величины:

.

Напряжение на индуктивности L найдем в соответствии с (2):

.

Меняя местами операции взятия производной и выделения действительной части, получим далее

. (24)

Из (24) видно, что величину V_L(t)можно рассматривать как действительную часть комплексного выражения , где комплексная амплитуда имеет вид

. (25)

В (25) учтено, что в соответствии с формулой Эйлера

.

Из (24) и (25) следует, что напряжение на индуктивности меняется по гармоническому закону с той же частотой, что и ток, но опережает ток по фазе на :

. (26)

Амплитуда напряжения V₀ cвязана с амплитудой тока формулой

V₀ = I₀ L. (27)

Фазовому (26) и амплитудному (27) соотношениям напряжения и тока можно придать более компактную форму:

.

Величина называется индуктивным сопротивлением или импедансом индуктивности.

На рис. 12а, в соответствии с идеей метода векторных диаграмм показаны векторы тока и напряжения на индуктивности. Физической причиной, приводящей к отставанию тока по фазе от напряжения, является эффект самоиндукции, препятствующий мгновенному изменению тока в фазе с приложенным напряжением.

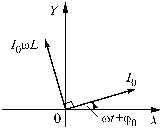
а)

 

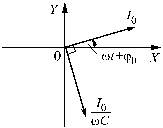
б)

в)

Рис. 12. Метод векторных диаграмм: а - векторы тока и напряжения на индуктивности. Ток отстает по фазе от напряжения; б - векторы тока и напряжения на емкости. Напряжение отстает по фазе от тока; в - векторы тока и напряжения на сопротивлении. Ток и напряжение синфазны

Емкость. Гармоническое напряжение

V_c(t) = V₀ cos ( )

на конденсаторе представим как действительную часть комплексной величины

.

Заряд на обкладках конденсатора запишем как

.

Ток, текущий в цепи конденсатора, найдем дифференцированием заряда по времени и перестановкой местами операций d/dt и Re:

.

Отсюда видно, что комплексные амплитуды тока и напряжения на конденсаторе связаны соотношением

,

или

. (28)

Таким образом, напряжение и ток на емкости изменяются по гармоническому закону с одинаковой частотой и, как показывает (28), напряжение отстает от тока по фазе на .

Комплексная форма записи соотношения напряжения и тока на емкости имеет вид

,

где z_c = 1/i C - емкостное сопротивление, или импеданс емкости.

На рис. 12б, методом векторных диаграмм представлено фазовое соотношение тока и напряжения на емкости. Напряжение отстает по фазе от тока, так как оно пропорционально заряду на конденсаторе, а для накопления заряда необходимо время.

Сопротивление. Из соотношения (4) следует, что ток и напряжение на сопротивлении всегда синфазны. Связь между комплексными амплитудами напряжения и тока в этом случае имеет вид

,

где z_R = R - сопротивление.

На рис. 12в, приведена векторная диаграмма для случая синфазных тока и напряжения.

Генератор гармонического напряжения. Генерируемому на выходе такого источника напряжению

(t) =  ₀ cos ( )

можно поставить в соответствие комплексное выражение

,

но, как указывалось ранее, эта величина не зависит от тока, текущего в цепи. Поэтому нельзя ввести величину импеданса источника.

Правила Кирхгофа для цепей переменного гармонического тока. Поскольку токи и напряжения на элементах цепи изменяются с одинаковой частотой, правила Кирхгофа (6) и (8) могут быть представлены в комплексной форме с помощью комплексных амплитуд:

; (29)

. (30)

Заметим, что правила (29) и (30) не содержат временных зависимостей и в этом смысле полностью соответствуют аналогичным законам для цепей постоянного тока. Поэтому методы расчета цепей постоянного тока могут быть применены для расчета цепей гармонического (синусоидального) тока, но с использованием алгебры комплексных чисел. В частности, при последовательном соединении двух каких-либо пассивных элементов величина результирующего импеданса равна сумме импедансов этих элементов:

z = z₁ + z₂ ,

а при параллельном соединении этих элементов величина обратного значения импеданса такого участка цепи равна сумме обратных значений импедансов элементов:

.