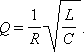14.3 Свободные гармонические колебания

Если внешний источник ЭДС отсутствует, то уравнение (11) (линейное и однородное относительно , , ) описывает свободные затухающие колебания. Если же нет и омического сопротивления, То есть в контуре нет потерь электромагнитной энергии (R = 0), то уравнение (11) принимает вид

(12)

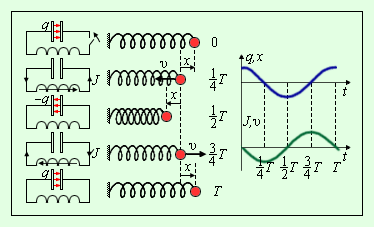
Уравнение (12) описывает свободные колебания в LC-контуре в отсутствие затухания. По виду оно в точности совпадает с уравнением свободных колебаний груза на пружине в отсутствие сил трения. Рис.  иллюстрирует аналогию процессов свободных электрических и механических колебаний. На рисунке приведены графики изменения заряда q (t) конденсатора и смещения x (t) груза от положения равновесия, а также графики тока J (t) и скорости груза υ (t) за один период колебаний.

Рисунок Аналогия процессов свободных электрических и механических колебаний

Система, поведение которой описывается уравнением (12), называется гармоническим осциллятором. Решение уравнения (12)

q(t) = q₀ cos  (13)

описывает гармонические колебания зарядов на обкладках конденсатора.

Две независимые постоянные q₀ и в (13) определяются начальными условиями. Если в качестве начальных условий взять значение заряда q(0) и тока I(0) в момент времени t = 0, то

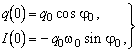
откуда

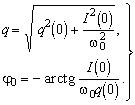(14)

Из (10) следует, что собственная частота гармонических колебаний выражается через величины L и С формулой

. (15)

Так как период колебаний Т₀ связан с циклической частотой соотношением , то из (15) следует формула У. Томсона (Кельвина):

.

Величина q₀ в (13), определяющая максимальное (положительное) значение заряда q(t), называется амплитудой заряда, а величина - фазой колебаний заряда ( - начальная фаза).

Важно иметь в виду, что собственная частота гармонических колебаний зависит только от свойств самой колебательной системы (см. формулу (15)), в то время как амплитуда заряда q₀и начальная фаза колебаний заряда определяются не столько свойствами системы, сколько начальными условиями (см. формулу (14) и рис. 7).

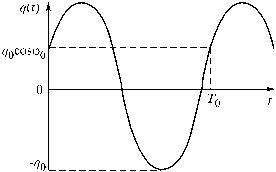
Рис. 7. График зависимости заряда на пластине конденсатора от времени - свободные гармонические колебания. Заряд в начальный момент связан с амплитудой заряда и начальной фазой колебаний заряда

14.4 Свободные затухающие колебания

С учетом омического сопротивления уравнение колебательного контура записывается в виде

. (17)

Для его анализа введем вспомогательную функцию (t) в соответствии с формулой

.

Подставляя последнюю в (17), получим для (t)дифференциальное уравнение

, (18)

которое формально совпадает с уравнением (12), но с коэффициентом , принимающим как положительные, так и отрицательные значения.

При введем новую величину в соответствии с формулой .

При этом уравнения (12) и (18) совпадают, а значит, совпадают и их решения. Следовательно,

(t) = q₀ cos ( ).

Таким образом, решение уравнения (17) имеет вид

. (19)

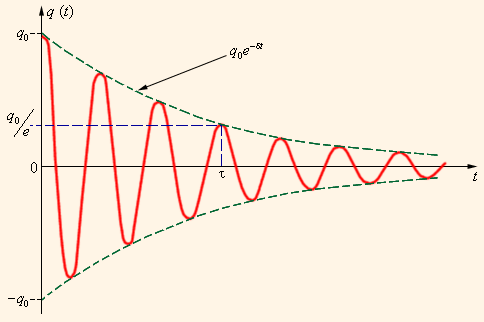
График функции (19), представленный на рис. 8, свидетельствует о том, что она непериодична. Однако величина q периодически проходит через нуль, достигая в промежутках минимальных и максимальных значений. В этом смысле процесс, описываемый выражением (19), является колебательным. Такие свободные затухающие колебания могут быть охарактеризованы периодом, равным удвоенному времени между двумя последовательными прохождениями величины q(t) через нуль (Приравнивая нулю, можно убедиться в том, что период Т есть время между двумя последовательными максимальными (или двумя последовательными минимальными) значениями величины q(t)):

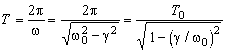. (20)

Все реальные контуры содержат электрическое сопротивление R. Процесс свободных колебаний в таком контуре уже не подчиняется гармоническому закону. За каждый период колебаний часть электромагнитной энергии, запасенной в контуре, превращается в джоулево тепло, и колебания становятся затухающими (рис. 8).

Рис. 8. График зависимости заряда на пластине конденсатора от времени - свободные затухающие колебания. Пунктиром показан график зависимости амплитуды затухающих колебаний заряда

Множитель в формуле (19) называют амплитудой затухающих колебаний заряда. Она экспоненциально убывает во времени, уменьшаясь в е раз за время

,

называемое временем затухания (временем релаксации). Число колебаний, совершаемых за время , равно

.

Логарифм отношения амплитуд в моменты прохождения величины q(t) через соседние максимумы называют логарифмическим декрементом затухания:

.

Величина

(21)

называется добротностью колебательного контура, можно записать

где N – число полных колебаний, совершаемых системой за время затухания τ. Добротности Q любой колебательной системы, способной совершать свободные колебания, может быть дано энергетическое определение:

Для RLC-контура добротность Q выражается формулой

Добротность электрических контуров, применяемых в радиотехнике, обычно порядка нескольких десятков и даже сотен.

Следует отметить, что собственная частота ω свободных колебаний в контуре с не очень высокой добротностью несколько меньше собственной частоты ω₀ идеального контура с теми же значениями L и C. Но при Q ≥ (5÷10) этим различием можно пренебречь.

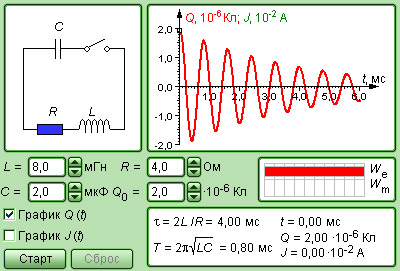
Модель. Свободные колебания в RLC-контуре ПОЯСНЕНИЯ К МОДЕЛИ

Модель предназначена для изучения свободных колебаний в последовательном RLC-контуре при различных значениях параметров.

В идеальном контуре без потерь (R = 0) свободные незатухающие колебания происходят на частоте При наличии потерь (R ≠ 0) в контуре свободные колебания становятся затухающими. Амплитуда колебаний уменьшается во времени по экспоненциальному закону. Время, за которое амплитуда колебаний уменьшается в e = 2,7 раза, называется временем затухания. Оно равно τ = 2L / R.

В компьютерной модели можно изменять величины R, L и C, а также первоначальный заряд конденсатора Q₀. На дисплее высвечиваются графики Q (t) и тока J (t). Ток J (t) в цепи опережает заряд Q (t) конденсатора по фазе на угол π / 2. Обратите внимание, что два раза за период происходит процесс перекачки электрической энергии, запасенной в конденсаторе, в магнитную энергию катушки и обратно.