14.1.3 Правила Кирхгофа для цепей квазистационарного тока.

Pассмотрим электрическую цепь, состоящую из сосредоточенных элементов R, L, C, (t), cоединенных идеальными проводниками (не обладающими ни сопротивлением, ни индуктивностью, ни емкостью). В любой цепи такого рода можно обнаружить контуры и узлы. Контуром называется замкнутый участок электрической цепи, а узлом - точка, в которой соединено больше двух проводов.

Первое правило Кирхгофа. Так как электрическая емкость узла равна нулю, то заряд не может накапливаться в узле и в соответствии с законом сохранения заряда результирующий поток заряда через замкнутую поверхность, охватывающую любой узел цепи, равен нулю, т.е. алгебраическая сумма токов в узле равна нулю:

(6)

Здесь индексом k обозначены номера токов, сходящихся в узле, а алгебраические знаки входящих и выходящих токов противоположны.

Второе правило Кирхгофа. Одним из важнейших свойств сосредоточенных элементов цепи квазистационарного тока, проанализированного ранее, является отсутствие вне элементов меняющихся со временем электрических и магнитных полей. Это свойство приводит к тому, что циркуляция поля по любому замкнутому контуру, связывающему выводные клеммы сосредоточенных элементов любой замкнутой цепи, равна нулю. Поэтому

, (7)

где U_k - напряжение на любом сосредоточенном элементе цепи с индексом k. Учитывая, что для активных элементов выполняется равенство (5), и оставляя в левой части равенства (7) суммы только по пассивным, а в правой части только по активным элементам, запишем окончательно

. (8)

14.2 Уравнение колебательного контура

В широком смысле под колебанием понимают любой процесс, в котором значения физических величин, описывающих состояние системы, повторяются через равные (периодический процесс) или приблизительно равные (квазипериодический процесс) промежутки времени.

Например, поток Ф вектора магнитного поля через плоскость рамки площадью S (рис. 5), вращающейся с постоянной угловой скоростью в постоянном и однородном магнитном поле, периодически изменяется со временем:

.

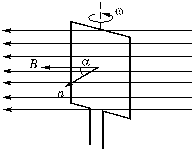
Рис. 5. Рамка равномерно вращается в магнитном поле

Здесь учтено, что при равномерном вращении угол поворота пропорционален времени: .

В соответствии с одним из уравнений Максвелла (закон электромагнитной индукции Фарадея - Ленца) в рамке возбуждается электродвижущая сила индукции

и электрический ток

Здесь введены обозначения и (R - сопротивление рамки). Таким образом, можно говорить о колебаниях периодически меняющихся физических величин Ф(t),  (t), I(t).

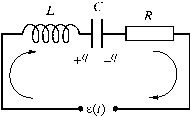
Рис. 6. Последовательный RLC контур, подключенный к источнику переменной ЭДС

Рассмотрим колебательный контур (рис. 6), состоящий из последовательно соединенных идеальных индуктивности L, емкости С и резистора R, подключенный к источнику ЭДС, напряжение которого является заданной функцией времени (t). При выполнении условия квазистационарности на основании второго правила Кирхгофа получим

.

Принимая во внимание, что I = dq / dt, придем к уравнению колебательного контура:

, (9)

которое является линейным дифференциальным уравнением второго порядка.

Вводя обозначения

; ; , (10)

уравнение (9) представим в приведенном виде:

. (11)

В форме (11) уравнение колебательного контура совпадает с уравнением вынужденных колебаний гармонического осциллятора с затуханием. Величина называется собственной частотой гармонических колебаний, а - коэффициентом затухания.