Емкость.

На концах a и b (рис. 2) удаленных выводов идеальной емкости С с квазистационарным током I(t) возникает разность потенциалов, равная Q/C.

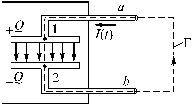
Рис. 2. Идеальная емкость и вспомогательный контур Г

Для доказательства рассмотрим контур Г с направлением обхода, совпадающим с направлением тока. (Заметим, что на рис. 2 изображен момент зарядки конденсатора, поэтому I(t) = dQ / dt.) Циркуляция электрического поля по контуру Г может быть представлена в виде

.

Проводники а1 и 2b не обладают сопротивлением, поэтому в соответствии с законом Ома первый и третий интегралы в правой части равенства равны нулю. Второй интеграл в квазистационарном режиме, как и в электростатике, может быть записан в виде

.

Четвертый интеграл, изображающий напряжение между концами а и b, может трактоваться как разность потенциалов:

.

Такая возможность появляется в связи с тем, что емкость считается сосредоточенной и вихревое электрическое поле вдали от нее исчезающе мало. Что же касается циркуляции поля по контуру Г, то она равна нулю в соответствии с уравнением Максвелла

и предположением об идеальности емкости, т.е. о том, что L = 0.

Таким образом, приходим к выражению для напряжения на емкости:

  (3)

Сопротивление.

На концах а, b (рис. 3) удаленных выводов идеального сопротивления R с квазистационарным током I(t) возникает разность потенциалов, равная IR.

Рис. 3. Идеальное сопротивление и вспомогательный контур Г

Для доказательства рассмотрим контур Г с направлением обхода, совпадающим с направлением тока. Циркуляцию электрического поля по контуру Г представим в виде

.

Первый и третий интегралы в правой части равенства равны нулю, так как закон Ома для участков a1и 2b, не обладающих сопротивлением, дает . На участке 12 внутри сопротивления находим

.

Здесь учтено, что j = I / S, , а также, что векторы и коллинеарны. Как и для случая постоянного тока, выражение имеет смысл сопротивления R участка 12. Наконец, примем во внимание, что коэффициент самоиндукции L рассматриваемой цепи a12b равен нулю, а значит, в соответствии с уравнением Максвелла (или интегральной формой записи закона Фарадея)

см. Основные формулы и соответствующую лекцию

циркуляция электрического поля по контуру Г равна нулю. Учтем также, что участок ab контура Г расположен вдали от сосредоточенного сопротивления и погружен в практически безвихревое поле . В результате оказывается, что напряжение не зависит от конфигурации внешнего участка контура Г между точками a и b.

Таким образом, для напряжения на сопротивлении имеем

(4)

Источник питания.

Условная схема типичного источника переменного напряжения приведена на рис. 4. Вращающийся с помощью внешнего устройства магнит создает изменяющийся поток магнитного поля через идеальную индуктивность. В результате между точками а и b возникает переменное напряжение.

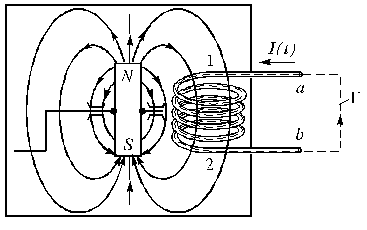
Рис. 4. Источник питания. Вращающийся магнит создает переменный магнитный поток через идеальную индуктивность

Покажем, что это напряжение не зависит от тока, текущего через источник, и может рассматриваться как разность потенциалов между точками а и b.

Рассмотрим контур Г, направление обхода которого совпадает с направлением тока I(t)(см. рис. 4). Будем пренебрегать собственным магнитным полем тока I(t) по сравнению с большим магнитным полем вращающегося магнита, так что именно последний создает переменный поток магнитного поля Ф_мг через витки индуктивности. Циркуляция поля по контуру Г в соответствии с уравнением Максвелла записывается в виде

Электродвижущая сила не зависит от тока I(t), текущего через источник. Кроме того, справедливо представление

.

Так как проводник a12b не обладает сопротивлением и подчиняется закону Ома, то равны нулю первые три интеграла в правой части равенства. Интеграл , вычисляемый по внешней части контура Г, не зависит от формы этой части, т.е. может рассматриваться как разность потенциалов:

.

Это следует из предположения, что рассматриваемый источник является сосредоточенным, т.е. не создает вне себя переменных, а следовательно, в соответствии с уравнениями Максвелла и вихревых полей.

Таким образом, разность потенциалов на клеммах источника является заданной функцией времени и не зависит от тока, текущего по цепи:

(5)

Принципиальное отличие напряжения на клеммах источника (5) от соответствующих выражений для напряжения на индуктивности (2), емкости (3) и сопротивлении (4) состоит в том, что его величина не зависит от величины тока и определяется только свойствами самого источника. Поэтому источник напряжения называют активным элементом цепи в отличие от остальных элементов, величина напряжения на которых зависит от величины тока или от характера его изменения со временем. В соответствии с этим индуктивность, емкость и сопротивление называют пассивными элементами цепи.