Тема 14. Квазистационарные процессы в цепях переменного тока

14.1 Условие квазистационарности

14.1.1 Разность потенциалов в квазистационарном электромагнитном поле

14.1.2 Правила Кирхгофа для цепей квазистационарного тока.

14.2 Уравнение колебательного контура

14.3 Свободные гармонические колебания

14.4 Свободные затухающие колебания

14.5 Векторный и комплексный методы описания гармонических колебаний

14.6 Вынужденные колебания в электромагнитном контуре

14.1.Условие квазистационарности

Рассмотрим случай, когда электромагнитное поле создается источниками (зарядами на обкладках конденсаторов, токами в соленоидах, отдельно движущимися зарядами и т.д.), состояние которых изменяется достаточно медленно. При этом электрическое поле в каждый момент времени практически зависит только от расположения зарядов в пространстве в тот же момент времени, т.е. совпадает с кулоновским полем неподвижных зарядов (как в электростатике), а магнитное поле определяется мгновенными значениями токов и скоростями движения зарядов (как в магнитостатике). Такое состояние электромагнитного поля реализуется вблизи от его источников в точках пространства, где как электрическое, так и магнитное поля устанавливаются за время, в течение которого положение и скорость зарядов, а также величины токов в источниках не успевают измениться. Другими словами, все изменения в источниках должны происходить настолько медленно, чтобы распространение электромагнитных возмущений до точки наблюдения можно было считать мгновенным:

 >> l / c, (1)

где - время, за которое состояние источников поля заметно изменяется; l - расстояние от источника до точки наблюдения; с - скорость распространения возмущения.

Такое электромагнитное поле называется квазистационарным, а неравенство (1) - условием квазистационарности.

Условие квазистационарности реализуется, например, в учебной лаборатории “Электромагнетизм”, где размеры лабораторных установок порядка метра, а частоты изменения электромагнитных полей лежат в звуковом диапазоне (менее 10⁵ Гц). Действительно, неравенство (1) в этом случае принимает вид

.

14.2 Разность потенциалов в квазистационарном электромагнитном поле

Рассмотрим свойства электрических цепей, основными элементами которых являются катушка индуктивности, конденсатор, резистор и источник напряжения. Эти элементы в дальнейшем будем называть просто индуктивностью, емкостью, сопротивлением и источником напряжения. Такая терминология обусловлена тем, что катушка индуктивности действительно обладает значительной индуктивностью и пренебрежимо малыми емкостью и сопротивлением. Аналогично конденсатор характеризуется малыми индуктивностью и сопротивлением, но ощутимой емкостью. Резистор же имеет малые как емкость, так и индуктивность, но заметное сопротивление. Перечисленные элементы соединяются проводниками, не обладающими ни сопротивлением, ни емкостью, ни индуктивностью. Конечно, такое представление отличается от действительности, но во многих случаях может служить удовлетворительным приближением к ней.

Хотя в квазистационарном режиме электрические и магнитные поля меняются со временем, тем не менее, для отдаленных концов выводов каждого из четырех названных выше элементов можно использовать понятие разности потенциалов. Рассмотрим подробнее обоснование этого утверждения для каждого элемента.

Индуктивность.

На концах а и b (рис. 1) удаленных выводов идеальной индуктивности L с квазистационарным током I(t) возникает разность потенциалов, равная .

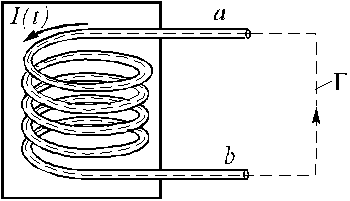
Рис. 1. Идеальная индуктивность и вспомогательный контур Г

Для доказательства рассмотрим контур Г, который одной своей частью проходит внутри провода, а другой - в области пространства, где практически отсутствует магнитное, а значит, и вихревое электрическое поле. Последнее свойство наблюдается в связи с тем, что концы а и b выводов индуктивности находятся достаточно далеко от нее. Это позволяет считать индуктивность сосредоточенным элементом цепи.

Пусть направление обхода контура Г совпадает с направлением тока I(t) (cм. рис. 1), тогда можно записать

.

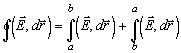Первый из интегралов в правой части равенства вычисляется вдоль траектории, расположенной в проводнике, где в соответствии с законом Ома - (закон Ома в дифференциальной форме, где -величина, обратная удельному сопротивлению называется удельной электрической проводимостью ) и отсутствием сопротивления у идеальной индуктивности справедливо утверждение . Второй интеграл в силу сосредоточенности индуктивности не зависит от формы внешнего участка контура Г (конечно, если не располагать этот участок вблизи от индуктивности) и поэтому может быть представлен в виде разности потенциалов ( ). Таким образом, с одной стороны, имеем

,

а с другой стороны, одно из уравнений Максвелла дает

.

В итоге для напряжения на индуктивности имеем

(2)