Алгебраический критерий Гурвица

Из хар-го уравнения строится матрица Гурвица:

Если все коэффициенты характеристического полинома положительны, а также больше нуля все определители матрицы Гурвица, то такая система будет устойчива.

С этим критерием удобно когда система не большого порядка.

Частотный критерий Михайлова

- функция Михайлова.

По функции Михайлова строится годограф Михайлова при зменении частоты от о до .

Если годограф для системы n^го порядка описывает в положительном направлении n квадрантов и начинается с положительной естественной полуоси, то такая система будет устойчива.

Частотный критерий Найквиста

По АФЧХ разомкнутой системы можно судить об устойчивости замкнутой системы. Если годограф АФЧХ разомкнутой системы не охватывает точку с координатами (-1, j0) на комплексной плоскости, то замкнутая система будет устойчива.

Если АФЧХ при увеличении частоты проходит этот участок сверху вниз, то такой участок будем называется положительным, в противном случае отрицательным. Если алгебраическая сумма положительных и отрицательных переходов равна , где - количество положительных корней у характеристического полинома, то система будет устойчивой.

4. Запас устойчивости аср. Понятие, назначение, способы определения по критерию Найквиста.

Устойчивость является необходимым условием нормального функционирования АСР. Поэтому устойчивость системы должна иметь место не только в случае постоянства ее параметров, но и тогда, когда они в процессе эксплуатации в определенных пределах изменяются. Иначе говоря, АСР должна обладать некоторым запасом устойчивости, обеспечивающим ее работоспособность в различных условиях эксплуатации. Введение запаса устойчивости имеет значение еще и потому, что обеспечивает работу системы со значительно меньшей колебательностью процесса регулирования, чем в случае ее работы в режиме, близком к границе устойчивости.

Запас устойчивости можно оценивать по критериям:

Гурвица:

Все определители должны быть больше положительного заданного числа.

Михайлова:

Задаются радиусом R, по которому строится окружность, и тогда круг будет запретной областью для годографа Михайлова. Чем болше R тем больше запас устойчивости.

Найквист:

Запас устойчивости по фазе ₃ определяется между отрицательным направлением действительной оси и лучом, проведенным через начало координат и точку пересечения годографа с окружностью единичного радиуса (т.е. через точку _ср). В системах запас по фазе составляет 30-60⁰.

Запас устойчивости по модулю R характеризует удаление годографа от критической точки в направлении действительной оси. В системах запас по модулю R составляет около 0.5-0.9

w пер- частота перехода, wср- частота среза (R=0), коэффициент передачи системы равен 1.

Следствие из критерия Найквиста - логарифмический критерий: система будет устойчива, если частота среза меньше частоты перехода ( ).

4. Области устойчивости (понятие, назначение). D-разбиение в плоскости одного параметра. Пример.

Для каждой конкретной АСР постоянные коэффициенты в характеристическом уравнении определяются типом и конструктивными особенностями регулятора, а также динамическими свойствами самого объекта управления. Причем часть этих коэффициентов может изменятся во времени в процессе эксплуатации системы, а другая часть может быть изменена в процессе настройки регулятора.

При проектировании системы и ее эксплуатации важно знать, в каких границах могут изменятся параметры при сохранении устойчивости АСР.

Области изменения этих параметров называются областями устойчивости.

Задача построения областей устойчивости решается с помощью так называемого метода D-разбиений, в основе которого лежит отображение мнимой оси с комплексной плоскости корней характеристического уравнения на действительную плоскость двух параметров или на плоскость одного параметра.

Для этого необходимо вместо P подставть j и отделив Re и Im-части полученной частотной функции построить ее годограф в диапазоне частот от - до +.

Область выделяется на основе правила штриховки симметричной кривой D-разбиений.

Кривая штрихуется слева при ее обходе с изменением частоты  от - до +.

В замкнутой области, образованной границей со штриховкой внутрь, рассматриваемая система будет устойчивой.

Пример.

вместо P подставим j и отделим Re и Im-части. Найдем корни мнимой части 1=0 2,3=+√3, тогда А=0-6

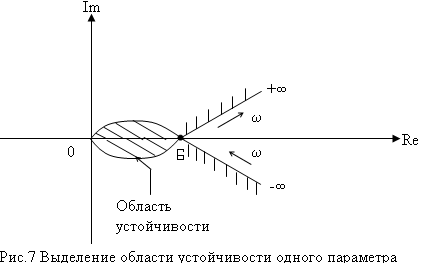
Теоретически параметр А является комплексной величиной. Однако из физических соображений ясно, что он должен быть вещественным. Это означает, что в рассмотрение вводиться отрезок вещественной оси 0 - 6.