4.4. Вычисление площадей с помощью палетки

Для определения площадей небольших участков с криволинейными контурами на плане применяют палетки, в основном прямолинейные. К прямолинейным палеткам относятся известные и наиболее распространенные квадратные и параллельные палетки.

Квадратная палетка представляет собой сеть взаимно перпендикулярных линий, проведенных через 1–2 мм на прозрачном целлулоиде, плексигласе, фотопленке, стекле или кальке.

Площадь фигуры определяется простым подсчетом клеток палетки, наложенной на фигуру. Доли клеток, рассекаемых контуром на части, учитываются на глаз (рис. 13). Квадратной палеткой не рекомендуется определять площади больше 2 см² на плане. Недостаток ее применения (помимо того, что площади долей клеток, рассекаемых контуром, приходится оценивать на глаз) в том, что подсчет количества целых клеток нередко сопровождается грубыми погрешностями.

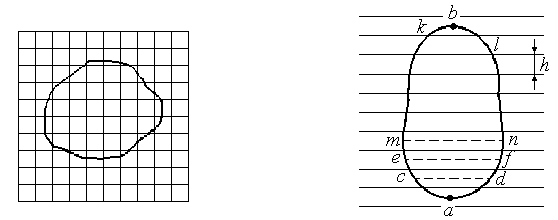
Рис. 13

Рис. 14

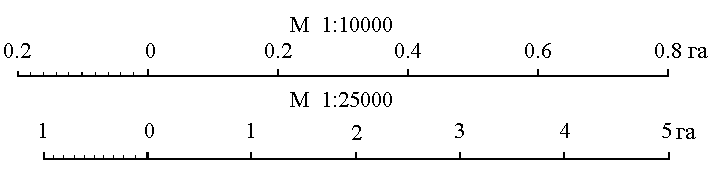
Рис. 15

Такие недостатки не наблюдаются при определении площадей параллельной палеткой, представляющей собой листок прозрачного целлулоида, плексигласа или кальки, на котором нанесены параллельные линии преимущественно через 2 мм одна от другой. Площадь контура определяют этой палеткой следующим образом. Накладывают ее на контур так, чтобы крайние точки a и b разместились посредине между параллельными линиями палетки. Тогда, весь контур оказывается разделенным параллельными линиями на фигуры, близкие к трапециям, с одинаковыми высотами, причем отрезки параллельных линий внутри контура являются средними линиями трапеций (рис.14). Пунктиром показаны основания этих трапеций.

Сумма площадей трапеций, т.е. площадь контура, равна

.

Следовательно, чтобы получить площадь контура, нужно взять сумму средних линий, т.е. сумму отрезков параллельных прямых внутри контура, и умножить на расстояние между ними.

Для упрощения определения площади сумму средних линий последовательно набирают в раствор циркуля, которую определяют по масштабной линейке и полученную длину умножают на h, м (рис.15). Чтобы не выполнять подобных вычислений, для каждого масштаба строят специальную шкалу, по которой отсчитывают площадь контура, зная сумму средних линий.

Расчет шкалы: М 1:10000, h = 2 мм, при длине шкалы 1 см площадь равна (0.2 см  100 м)  (1 см  100 м) = 2000 м² = 0.2 га. Параллельной палеткой не следует определять площади больше 10 см² на плане.

4.5. Точность вычисления площадей графическим способом и с помощью палетки

При разбивке участка на простейшие фигуры точность вычисления для различных вариантов не будет одинаковой. Площадь треугольника графическим способом вычисляется точнее, чем площади других фигур. Следовательно, площадь при разбивке участка на треугольники вычисляется точнее, чем при разбивке на другие фигуры (трапеции, прямоугольники). При разбивке участка на треугольники из всех вариантов будет лучшим тот, в котором треугольники будут равносторонними или высота h примерно равна основанию a.

Погрешность уменьшается, если вычислять площадь треугольника не как , а по формуле Герона

,

где . Это дает уточнение до 13% даже для равностороннего треугольника. Основание треугольника может быть во много раз меньше высоты, если оно измеряется на местности, а не на плане.

При разбивке площади на треугольники погрешность площади участка

,

где M – знаменатель численного масштаба плана. Если вычисляют два раза, то.

Число треугольников, на которое разбивается участок, не влияет на погрешность площади. Поэтому при разбивке участка на треугольники не надо стремиться к тому, чтобы их было меньше. Точность однократного определения площади квадратной и параллельной палетками, а также ротометром характеризуется эмпирической формулой

.