Статистическая обработка данных в модулях Multiply Regression и Visual Stepwise Regression Analysis

Если все выше рассмотренные методы относятся к одномерной статистике, то далее методы будут многомерными, т.е. в анализы будет включено более трех переменных. В этом случае используются методы многофакторного анализа, которые позволяют выявить из большого числа независимых переменных наиболее значимые, а также оценить влияние факторов друг на друга.

С учетом того, что методы многомерной статистики требуют большого числа данных (выборки), то в дальнейшем студентам будет предложена готовая таблица в файле Litoral.STA, где содержатся данные обследования зообентоса литорали 137 малых озер Финской Лапландии (Приложение). Материал был получен путем сбора проб зообентоса с помощью ручного сачка на прибрежье озер с глубиной воды 0.1–1.5 м (Yakovlev, 1999).

Регрессионный анализ - наиболее часто используемый метод исследования закономерностей связи между явлениями (процессами), которые зависят от многих, зачастую неизвестных, факторов. Статистические зависимости описываются математическими моделями, т.е. регрессионными уравнениями. Задавая значения Х в уравнение прямолинейной регрессии (Y = a₁X₁ + a₂X₂ + a_nX_n + b), можно прогнозировать значения Y. Метод используется очень широко в биологии. Главное требование – ряды переменных должны подчиняться закону нормального распределения и не иметь резко выделяющихся по величине данные. Если распределение отличается от нормального, то оценка параметров модели, построенной методом наименьших квадратов, будет неточной.

Различают однофакторные и многофакторные регрессионные зависимости. Первый вид анализа был рассмотрен нами при изучении Excel (Занятие 11).

Задание 1. Постройте линейное уравнение зависимости числа видов зообентоса от абиотических факторов, характеризующих физико-химические показатели литорали малых озер.

• Откройте окно STATISTICA Module Switcher (Переключатель модуля) и выберите модуль Multiple Regression (Множественная регрессия).

• Нажмите кнопку Variables (Переменные) и выберите в левом окне зависимую переменную N_SP (число видов), а в правом окне Select dependent and independent variable lists: - переменные (абиотические факторы) с 5 по 18. Нажмите два раза кнопку ОК (рис. 47).

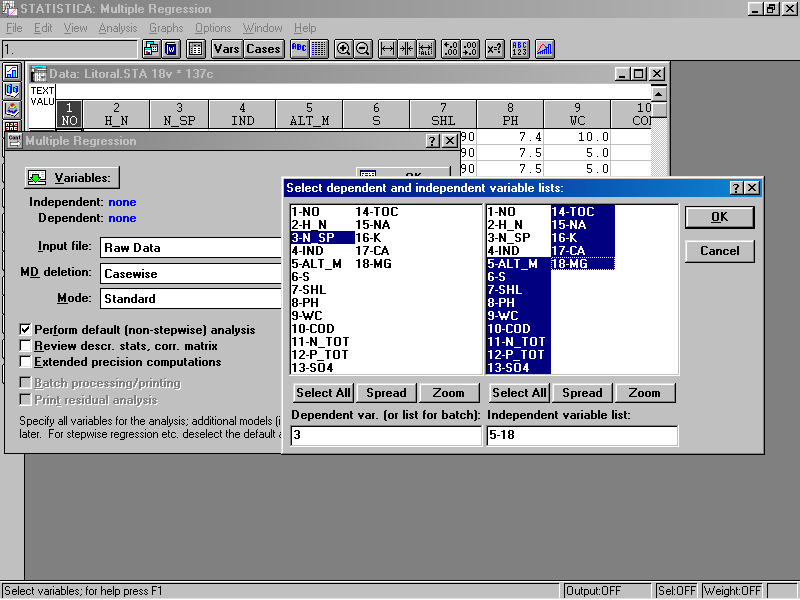
Рис. 47. Вид меню множественной регрессии и окна выбора списков зависимых и независимых переменных.

• В окне Multiple Regression Results (Результаты регрессионного анализа) представлены результаты анализа в численном виде (рис. 48).

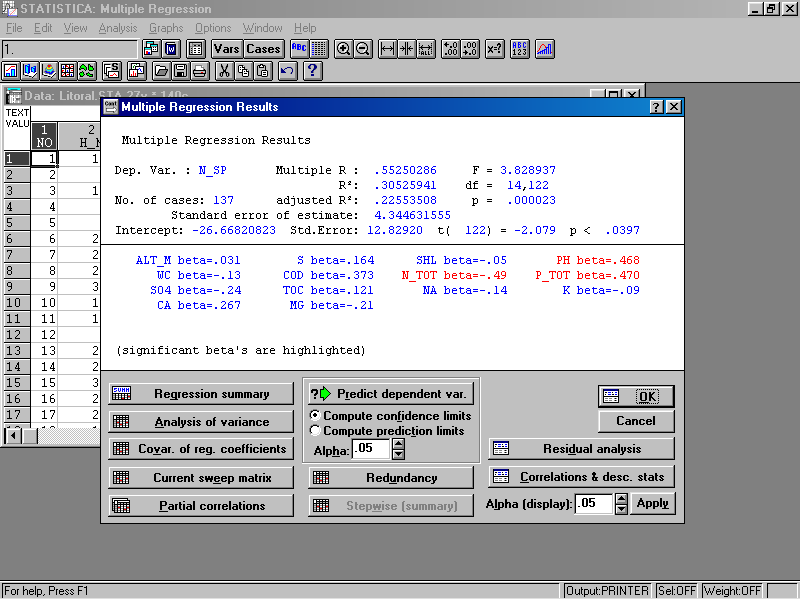
Рис. 48. Вид окна с результатами регрессионного анализа.

• Обратите внимание на цвета: красные – это значимые (p < 0.05) коэффициенты независимых переменных, а синие - незначимые. Число видов зообентоса находится в достоверной прямой зависимости от концентрации в воде азота (N_TOT), фосфора (P_TOT) и значения pH воды. Модель значима (р < 0.05). Однако величина коэффициента детерминации R² не так высока, составляет лишь 0. 31, т.е. значительна доля разброса относительного выборочного среднего зависимой переменной, объясняющей построенную регрессию. Качество построенной регрессии возрастает по мере приближения R² к 1. Свободный член регрессии (Intercept) равен -26.67.

• Выполните регрессионный анализ методом пошагового анализа (Stepwise Forward). Для этого нажмите кнопку Cancel в диалоговом окне Stepwise Regression Results (см. рис. 48).

• Задайте в окне Model Definition параметры как на рис. 49 и нажмите ОК.

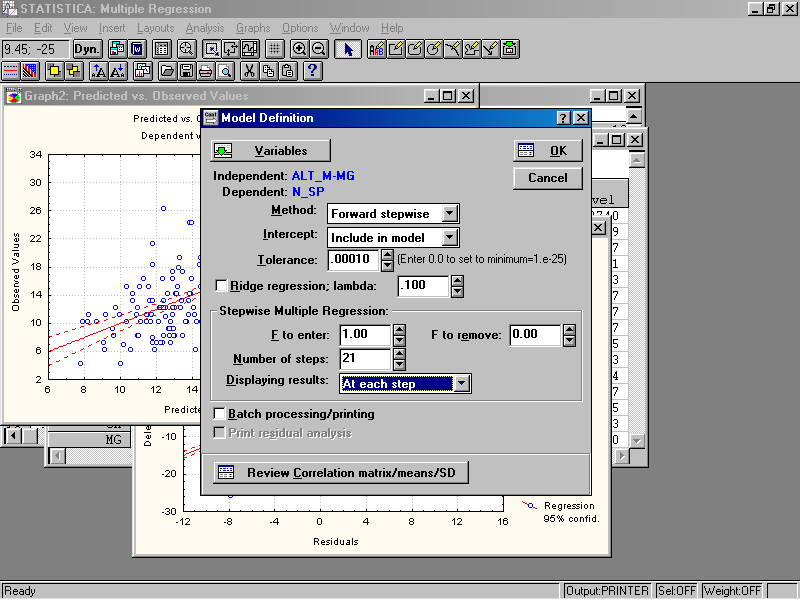
Рис. 49. Окно определения модели.

• Нажимайте кнопку Next до тех пор, пока не появится кнопка ОК. При каждом нажатии кнопки в окне будет появляться название новой переменной (красного цвета), включаемой в модель. После того, как будут выбраны переменные со значимыми вкладами, высветится ОК, нажмите еще раз (рис. 50). Появится окно Residual Analysis (Анализ остатков). Нажав кнопку Analysis Summary (Сводка анализа), выведите итоговую таблицу регрессии (рис. 51).

Верхнее окошко содержит следующую информацию.

RI или R² – это Квадрат коэффициента множественной корреляции или коэффициент детерминации. Значение его не так большое, т.е. построенная регрессия объясняет лишь 28.6% разброса значений переменной N_SP. Это свидетельствует о том, что на значения этой переменной большое влияние оказывают не включенные в модель факторы.

Std. Error – стандартная ошибка свободного члена регрессии (4.3).

р - уровень значимости (0.000).

Второе окно содержит значение свободного члена регрессии (Intercept), равное –26.4, и коэффициентов независимых переменных. При сравнении значений р, видно что наиболее значим вклад переменной pH, азота (N_TOT) и фосфора (P_TOT). Переменные S, TOC и Na можно не включать в модель без особого ущерба для точности. Но для этого придется снова выполнить новый расчет с оставшимися переменными.

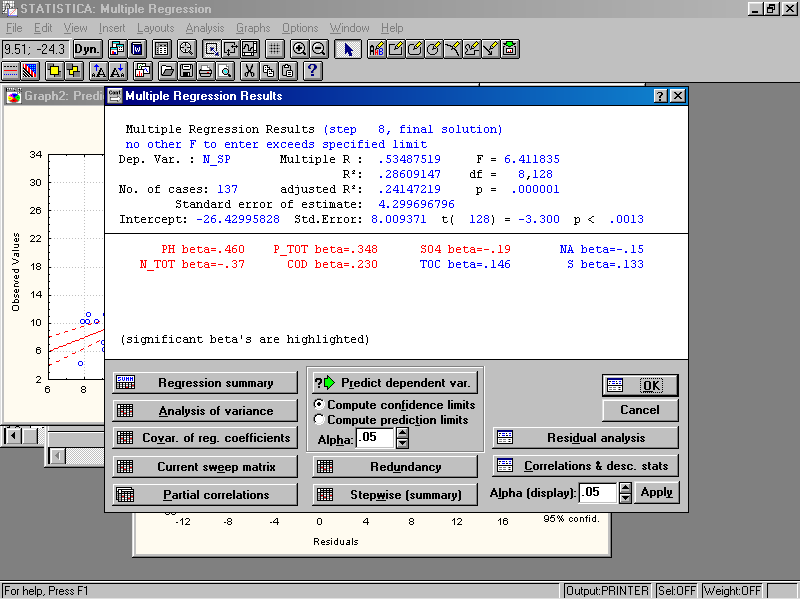
Рис. 50. Окно результатов множественной регрессии.

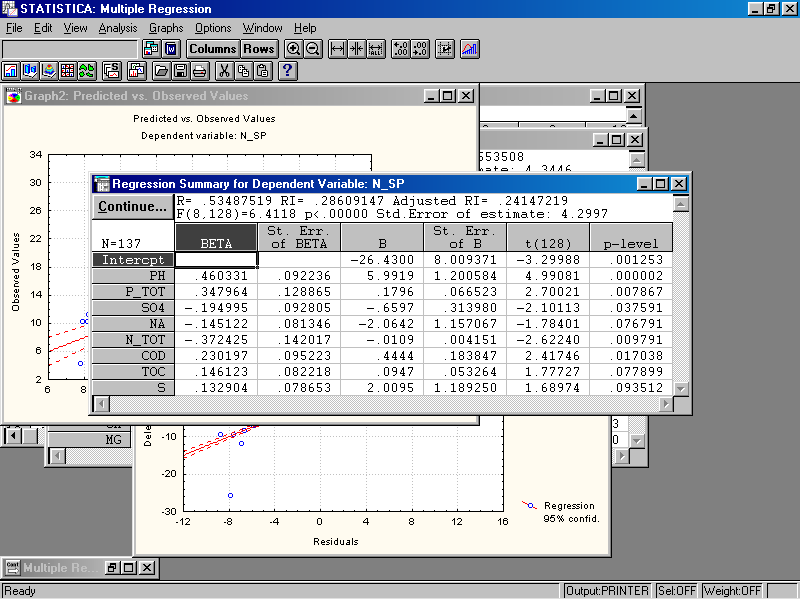
Рис. 51. Итоговая таблица для зависимой переменной N_SP.

В целом уравнение имеет вид:

N_SP = 6.0pH + 0.2P_TOT – 2.1NA – 0.01N_TOT + 0.4COD + 0.1TOC – 0.7SO4 + 0.01S –26.4.

Несмотря на то что ряд независимых переменных характеризуется незначимым вкладом, уравнение можно использовать для прогнозирования. Для проверки адекватности модели используют анализ остатков (Residual Analysis).

• Нажмите кнопку Residual Analysis, а затем Obs. & Resudals (G). На экране появится график, который показывает адекватность модели (рис. 52).

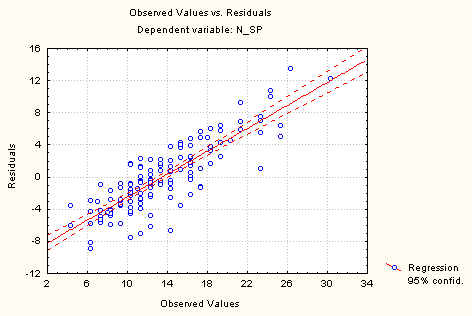
Рис. 52. График наблюдаемые переменные – остатки.

Занятие 17.