
- •Часть 2
- •Содержание
- •Введение
- •На основании теоремы для функции f(X), интегрируемой с квадратом на отрезке [-l, l], тригонометрическим многочленом наилучшего среднеквадратичного приближения является тригонометрический многочлен
- •Тригонометрический многочлен (6) с коэффициентами Фурье (7) представляет собой n-ю частичную сумму ряда Фурье, сходящегося к функции f(X) на отрезке [-l, l]:
- •Порядок выполнения лабораторной работы.
- •Варианты.
- •Порядок выполнения работы.
- •Типовой отчет.
- •Варианты.
- •Порядок выполнения работы.
- •Типовой отчет.
- •Варианты.
- •Порядок выполнения работы.
- •Типовой отчет.
- •Варианты.
- •Порядок выполнения работы.
- •Типовой отчет.
- •Варианты.
- •Порядок выполнения лабораторной работы.
- •Типовой отчет.
- •Варианты.
- •Вид рабочего листа ms Excel.
- •Лабораторная работа № 14
- •Элементы теории
- •Порядок выполнения лабораторной работы.
- •Типовой отчет.
- •Варианты.
- •Вид рабочего листа ms Excel.
- •Заключение
- •Литература
- •Часть 2
Порядок выполнения работы.
Пример. Результаты эксперимента представлены в виде таблицы значений переменных x и y :
-
xi
1
2
3
4
5
yi
7,1
27,8
62,1
110
161
Для семи вариантов аппроксимирующих зависимостей с двумя параметрами и методом наименьших квадратов определить их оптимальные значения, вычислить коэффициенты регрессии и оценки уклонения аппроксимирующих зависимостей от экспериментальных точек, на основе чего выбрать лучший вариант эмпирической формулы.
Вид рабочего листа MS Excel представлен на рисунке.
1. Оформим расчет для эмпирической формулы y = x + . Программирование расчетной области проведем, учитывая, что далее эта область будет копироваться для вариантов с преобразованием координат. В данном случае X = x, Y = y, = k, = b. В диапазоне А3:А13 располагаем заголовки строк. В диапазоне B3:F3 указываем номера экспериментальных точек, ячейка G3 = "Сумма". В диапазонах Н4:Н6 и Н11:Н13 располагаем названия параметров, получаемых в результате реализации МНК.
В диапазоне B4:F5
размещаем значения экспериментальных
точек. Вычисляем преобразованные
значения переменной Х
= х: ячейка
В6 = "=B4"
и протягиваем формулу в диапазон C6:F6.
Вычисляем преобразованные значения
переменной Y
= y:
ячейка В7 =
"=B5" и
протягиваем формулу в диапазон C7:F7.
Вычисляем значения
![]() :
ячейка В8 =
"=B6^2" и
протягиваем формулу в диапазон C8:F8.
Вычисляем значения
:
ячейка В8 =
"=B6^2" и
протягиваем формулу в диапазон C8:F8.
Вычисляем значения
![]() :
ячейка В9 =
"=B7^2" и
протягиваем формулу в диапазон C9:F9.
Вычисляем значения
:
ячейка В9 =
"=B7^2" и
протягиваем формулу в диапазон C9:F9.
Вычисляем значения
![]() :
ячейка В10 =
"0числяем
йаем формулу в диапаения х
точек.
:
ячейка В10 =
"0числяем
йаем формулу в диапаения х
точек.
Вычисляем коэффициент
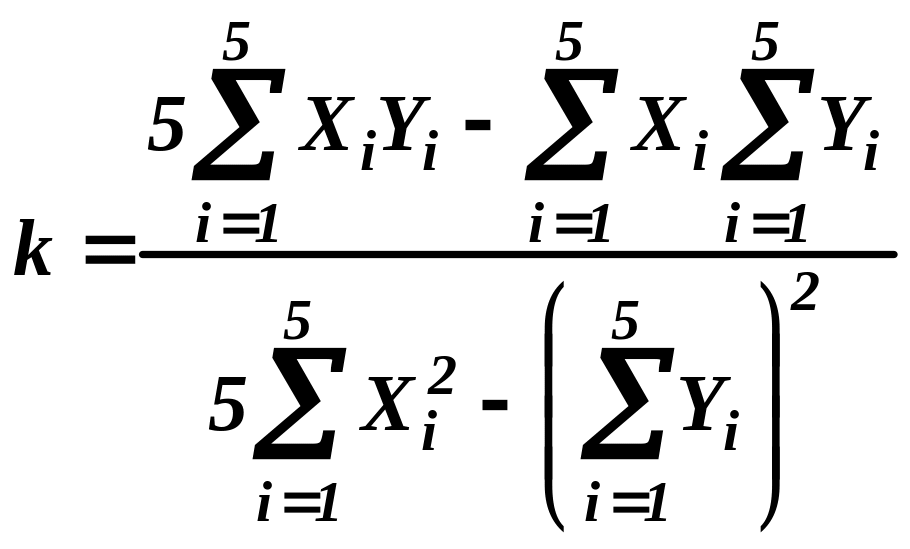 : ячейка I4
= "=(5*G10-G6*G7)/(5*G8-G6^2)".
Вычисляем коэффициент
: ячейка I4
= "=(5*G10-G6*G7)/(5*G8-G6^2)".
Вычисляем коэффициент
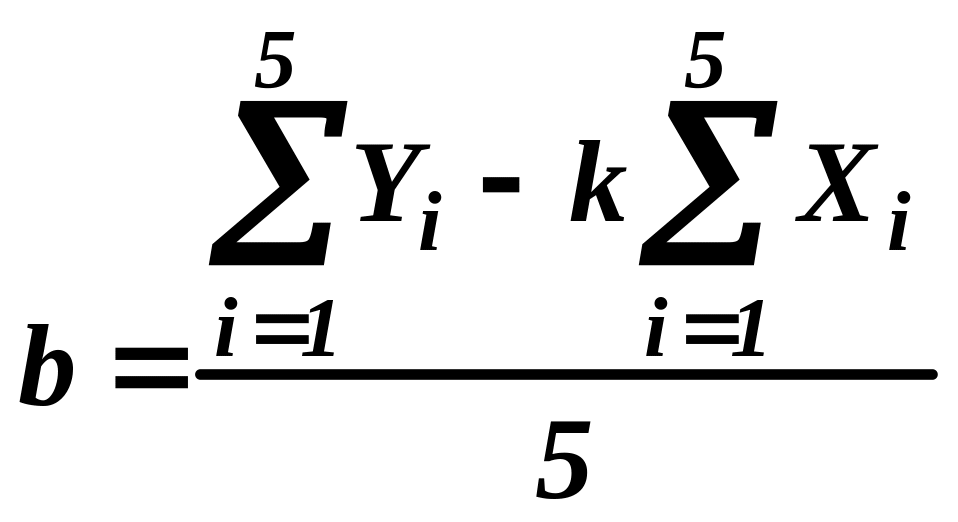 :
ячейка I5
= "=(G7-I4*G6)/5".
Вычисляем коэффициент регрессии
:
ячейка I5
= "=(G7-I4*G6)/5".
Вычисляем коэффициент регрессии
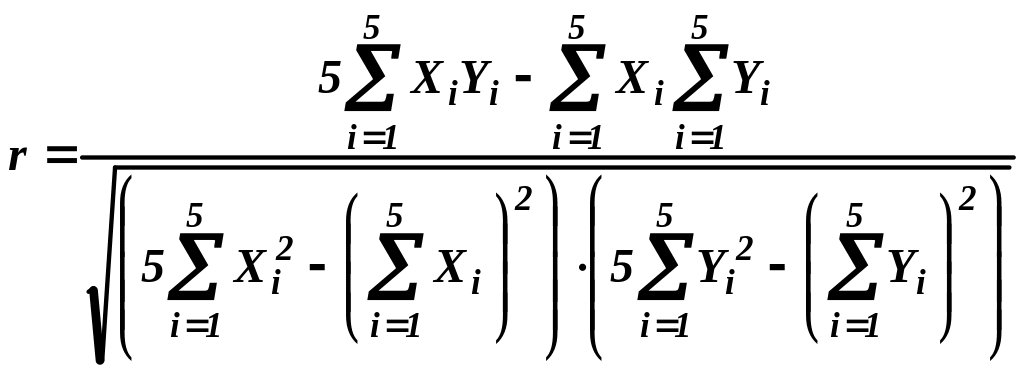 :
ячейка I6
= "=(5*G10-G6*G7)/КОРЕНЬ((5*G8-G6^2)*(5*G9-G7^2))".
Таким образом, рассчитана линейная
регрессия для преобразованных переменных.
:
ячейка I6
= "=(5*G10-G6*G7)/КОРЕНЬ((5*G8-G6^2)*(5*G9-G7^2))".
Таким образом, рассчитана линейная
регрессия для преобразованных переменных.
Программируем
переход к исходным переменным. Вычисляем
значение коэффициента
= k
исходной эмпирической формулы: ячейка
I11
= "=I4".
Вычисляем значение коэффициента
= b
исходной эмпирической формулы: ячейка
I12
= "=I5".
Вычисляем прогнозное значения исходной
зависимой переменной yпi
= xi
+
: ячейка В11
= "=$I$11*B4+$I$12"
и протягиваем формулу в диапазон C11:F11.
Вычисляем значения (
yi
– yпi)2:
ячейка В12 =
"=(B5-B11)^2"
и протягиваем формулу в диапазон C12:F12.
Вычисляем значения
![]() :
ячейка В13 =
"=B5^2" и
протягиваем формулу в диапазон C13:F13.
Вычисляем суммы всех определенных
величин протяжкой формулы из ячейки
G10
в диапазон G11:G13.
Вычисляем оценку уклонения аппроксимирующих
зависимостей от экспериментальных
точек по формуле
:
ячейка В13 =
"=B5^2" и
протягиваем формулу в диапазон C13:F13.
Вычисляем суммы всех определенных
величин протяжкой формулы из ячейки
G10
в диапазон G11:G13.
Вычисляем оценку уклонения аппроксимирующих
зависимостей от экспериментальных
точек по формуле
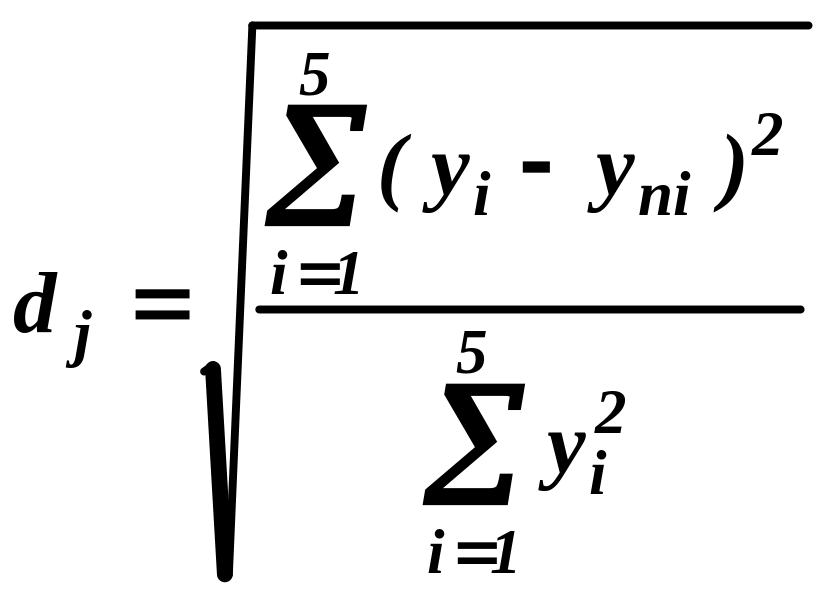 :
ячейка I13
= "=КОРЕНЬ(G12/G13)".
Строим графики заданной функции и
рассчитанной по методу наименьших
квадратов. Для этого выделяется диапазон
A4:F5,
при нажатой клавише Ctrl
выделяется диапазон A11:F11,
с помощью
мастера диаграмм строятся графики,
используя точечную диаграмму со
значениями, соединенными сглаженными
значениями без маркеров, и применяя
соответствующее форматирование графиков.
Исследование эмпирической формулы y
= x
+
закончено. Получено уравнение y
= 39 x
- 43,4 ;
оценка уклонения аппроксимирующей
зависимости от экспериментальных точек
d0
= 0,09749.
:
ячейка I13
= "=КОРЕНЬ(G12/G13)".
Строим графики заданной функции и
рассчитанной по методу наименьших
квадратов. Для этого выделяется диапазон
A4:F5,
при нажатой клавише Ctrl
выделяется диапазон A11:F11,
с помощью
мастера диаграмм строятся графики,
используя точечную диаграмму со
значениями, соединенными сглаженными
значениями без маркеров, и применяя
соответствующее форматирование графиков.
Исследование эмпирической формулы y
= x
+
закончено. Получено уравнение y
= 39 x
- 43,4 ;
оценка уклонения аппроксимирующей
зависимости от экспериментальных точек
d0
= 0,09749.
2. При исследовании
остальных аппроксимирующих формул
будем копировать диапазон исследования
предшествующей формулы ниже по рабочему
листу MS
Excel.
При этом изменяется содержимое следующих
ячеек (адресация дана по диапазону
исследования первой функции): заголовок
исследуемой функции А2,
номер мененыпирической
функцииной их формул будем копировать
предшествующий
диа
3. Исследуем формулу
![]() .
В данном примере диапазон A2:I33
копируется в ячейку А34.
При этом делаются следующие изменения.
Изменяем формулу преобразованной
переменной Y
= xy:
ячейка B39
= "=B36*B37" и
протягиваем формулу в диапазон C39:F39.
Изменяем формулу вычисления исходной
эмпирической функции
:
ячейка В43 =
"=$I$43+$I$44/B36" и
протягиваем формулу в диапазон C43:F43.
Получено уравнение
.
В данном примере диапазон A2:I33
копируется в ячейку А34.
При этом делаются следующие изменения.
Изменяем формулу преобразованной
переменной Y
= xy:
ячейка B39
= "=B36*B37" и
протягиваем формулу в диапазон C39:F39.
Изменяем формулу вычисления исходной
эмпирической функции
:
ячейка В43 =
"=$I$43+$I$44/B36" и
протягиваем формулу в диапазон C43:F43.
Получено уравнение
![]() ;
оценка уклонения аппроксимирующей
зависимости от экспериментальных точек
d1
= 0,56208.
;
оценка уклонения аппроксимирующей
зависимости от экспериментальных точек
d1
= 0,56208.
4. Исследуем формулу
![]() .
В данном примере диапазон A34:I65
копируется в ячейку А67.
При этом делаются следующие изменения.
Изменяем формулу преобразованной
переменной
.
В данном примере диапазон A34:I65
копируется в ячейку А67.
При этом делаются следующие изменения.
Изменяем формулу преобразованной
переменной
![]() :
ячейка B72
= "=1/B70" и
протягиваем формулу в диапазон C72:F72.
Изменяем формулу вычисления исходной
эмпирической функции
:
ячейка В76 =
"=1/($I$76*B69+$I$77)" и
протягиваем формулу в диапазон C76:F76.
Получено уравнение
:
ячейка B72
= "=1/B70" и
протягиваем формулу в диапазон C72:F72.
Изменяем формулу вычисления исходной
эмпирической функции
:
ячейка В76 =
"=1/($I$76*B69+$I$77)" и
протягиваем формулу в диапазон C76:F76.
Получено уравнение
![]() ;
оценка уклонения аппроксимирующей
зависимости от экспериментальных точек
d2
= 1,08032.
;
оценка уклонения аппроксимирующей
зависимости от экспериментальных точек
d2
= 1,08032.
5. Исследуем формулу
![]() .
В данном примере диапазон A67:I98
копируется в ячейку А100.
При этом делаются следующие изменения.
Изменяем формулу преобразованной
переменной
.
В данном примере диапазон A67:I98
копируется в ячейку А100.
При этом делаются следующие изменения.
Изменяем формулу преобразованной
переменной
![]() :
ячейка B105
= "=B102/B103" и
протягиваем формулу в диапазон C105:F105.
Изменяем формулу вычисления исходной
эмпирической функции
:
ячейка В109 =
"=B102/($I$109*B102+$I$110)" и
протягиваем формулу в диапазон C109:F109.
Получено уравнение
:
ячейка B105
= "=B102/B103" и
протягиваем формулу в диапазон C105:F105.
Изменяем формулу вычисления исходной
эмпирической функции
:
ячейка В109 =
"=B102/($I$109*B102+$I$110)" и
протягиваем формулу в диапазон C109:F109.
Получено уравнение
![]() ;
оценка уклонения аппроксимирующей
зависимости от экспериментальных
точек
d3
= 0,87564.
;
оценка уклонения аппроксимирующей
зависимости от экспериментальных
точек
d3
= 0,87564.
6. Исследуем формулу
![]() .
В данном примере диапазон A100:I131
копируется в ячейку А132.
При этом делаются следующие изменения.
Изменяем формулу преобразованной
переменной
.
В данном примере диапазон A100:I131
копируется в ячейку А132.
При этом делаются следующие изменения.
Изменяем формулу преобразованной
переменной
![]() :
ячейка B137
= "=LN(B135)" и
протягиваем формулу в диапазон C137:F137.
Изменяем коэффициент
:
ячейка B137
= "=LN(B135)" и
протягиваем формулу в диапазон C137:F137.
Изменяем коэффициент
![]() :
ячейка I141
= "=EXP(I135)".
Изменяем коэффициент
:
ячейка I141
= "=EXP(I135)".
Изменяем коэффициент
![]() :
ячейка I142
= "=EXP(I134)".
Изменяем формулу вычисления исходной
эмпирической функции
:
ячейка В141 =
"=$I$141*$I$142^B134" и
протягиваем формулу в диапазон C141:F141.
Получено уравнение
:
ячейка I142
= "=EXP(I134)".
Изменяем формулу вычисления исходной
эмпирической функции
:
ячейка В141 =
"=$I$141*$I$142^B134" и
протягиваем формулу в диапазон C141:F141.
Получено уравнение
![]() ;
оценка уклонения аппроксимирующей
зависимости от экспериментальных точек
d4
= 0,27098.
;
оценка уклонения аппроксимирующей
зависимости от экспериментальных точек
d4
= 0,27098.
7. Исследуем формулу
![]() .
В данном примере диапазон A132:I163
копируется в ячейку А165.
При этом делаются следующие изменения.
Изменяем формулу преобразованной
переменной X
= ln
x:
ячейка B169
= "=LN(B167)" и
протягиваем формулу в диапазон C169:F169.
Изменяем формулу преобразованной
переменной Y
= y
: ячейка
B170
= "=B168" и
протягиваем формулу в диапазон C170:F170.
Изменяем коэффициент
= k
: ячейка
I174
= "=I167".
Изменяем коэффициент
= b
: ячейка I175
= "=I168".
Изменяем формулу вычисления исходной
эмпирической функции
:
ячейка В174 =
"=$I$174*LN(B167)+$I$175" и
протягиваем формулу в диапазон C174:F174.
Получено уравнение
.
В данном примере диапазон A132:I163
копируется в ячейку А165.
При этом делаются следующие изменения.
Изменяем формулу преобразованной
переменной X
= ln
x:
ячейка B169
= "=LN(B167)" и
протягиваем формулу в диапазон C169:F169.
Изменяем формулу преобразованной
переменной Y
= y
: ячейка
B170
= "=B168" и
протягиваем формулу в диапазон C170:F170.
Изменяем коэффициент
= k
: ячейка
I174
= "=I167".
Изменяем коэффициент
= b
: ячейка I175
= "=I168".
Изменяем формулу вычисления исходной
эмпирической функции
:
ячейка В174 =
"=$I$174*LN(B167)+$I$175" и
протягиваем формулу в диапазон C174:F174.
Получено уравнение
![]() ;
оценка уклонения аппроксимирующей
зависимости от экспериментальных точек
d5
= 0,23137.
;
оценка уклонения аппроксимирующей
зависимости от экспериментальных точек
d5
= 0,23137.
8. Исследуем формулу
![]() .
В данном примере диапазон A165:I196
копируется в ячейку А197.
При этом делаются следующие изменения.
Изменяем формулу преобразованной
переменной Y
= ln
y
: ячейка
B202
= "=LN(B200)" и
протягиваем формулу в диапазон C202:F202.
Изменяем коэффициент
= e
b
: ячейка
I206
= "=EXP(I200)".
Изменяем коэффициент
= k
: ячейка I207
= "=I199".
Изменяем формулу вычисления исходной
эмпирической функции
:
ячейка В206 =
"=$I$206*B199^$I$207" и
протягиваем формулу в диапазон C206:F206.
Получено уравнение
.
В данном примере диапазон A165:I196
копируется в ячейку А197.
При этом делаются следующие изменения.
Изменяем формулу преобразованной
переменной Y
= ln
y
: ячейка
B202
= "=LN(B200)" и
протягиваем формулу в диапазон C202:F202.
Изменяем коэффициент
= e
b
: ячейка
I206
= "=EXP(I200)".
Изменяем коэффициент
= k
: ячейка I207
= "=I199".
Изменяем формулу вычисления исходной
эмпирической функции
:
ячейка В206 =
"=$I$206*B199^$I$207" и
протягиваем формулу в диапазон C206:F206.
Получено уравнение
![]() yобладает
функция
yобладает
функция
Наименьшей оценкой уклонения аппроксимирующей зависимости от экспериментальных точек, равной d6 = 0,0279 , обладает функция .
