
- •Часть 2
- •Содержание
- •Введение
- •На основании теоремы для функции f(X), интегрируемой с квадратом на отрезке [-l, l], тригонометрическим многочленом наилучшего среднеквадратичного приближения является тригонометрический многочлен
- •Тригонометрический многочлен (6) с коэффициентами Фурье (7) представляет собой n-ю частичную сумму ряда Фурье, сходящегося к функции f(X) на отрезке [-l, l]:
- •Порядок выполнения лабораторной работы.
- •Варианты.
- •Порядок выполнения работы.
- •Типовой отчет.
- •Варианты.
- •Порядок выполнения работы.
- •Типовой отчет.
- •Варианты.
- •Порядок выполнения работы.
- •Типовой отчет.
- •Варианты.
- •Порядок выполнения работы.
- •Типовой отчет.
- •Варианты.
- •Порядок выполнения лабораторной работы.
- •Типовой отчет.
- •Варианты.
- •Вид рабочего листа ms Excel.
- •Лабораторная работа № 14
- •Элементы теории
- •Порядок выполнения лабораторной работы.
- •Типовой отчет.
- •Варианты.
- •Вид рабочего листа ms Excel.
- •Заключение
- •Литература
- •Часть 2
Варианты.
Найти ряд Фурье функции f(x), представить графические приближения этой функции с помощью тригонометрических многочленов степени n = 15. Оценить погрешность и точность полученных приближений.
1. |
|
2. |
разложить по косинусам |
3. |
разложить по косинусам |
4. |
|
5. |
|
6. |
|
7. |
разложить по косинусам |
8. |
, разложить по синусам |
9. |
|
10. |
|
11. |
|
12. |
|
13. |
|
14. |
разложить по косинусам |
15. |
|
16. |
|
17. |
|
18. |
|
19. |
|
20. |
|
21. |
|
22. |
|
23. |
|
24. |
|
25. |
|
|
|
Вид расчетного листа MS Exсel для примера 1.
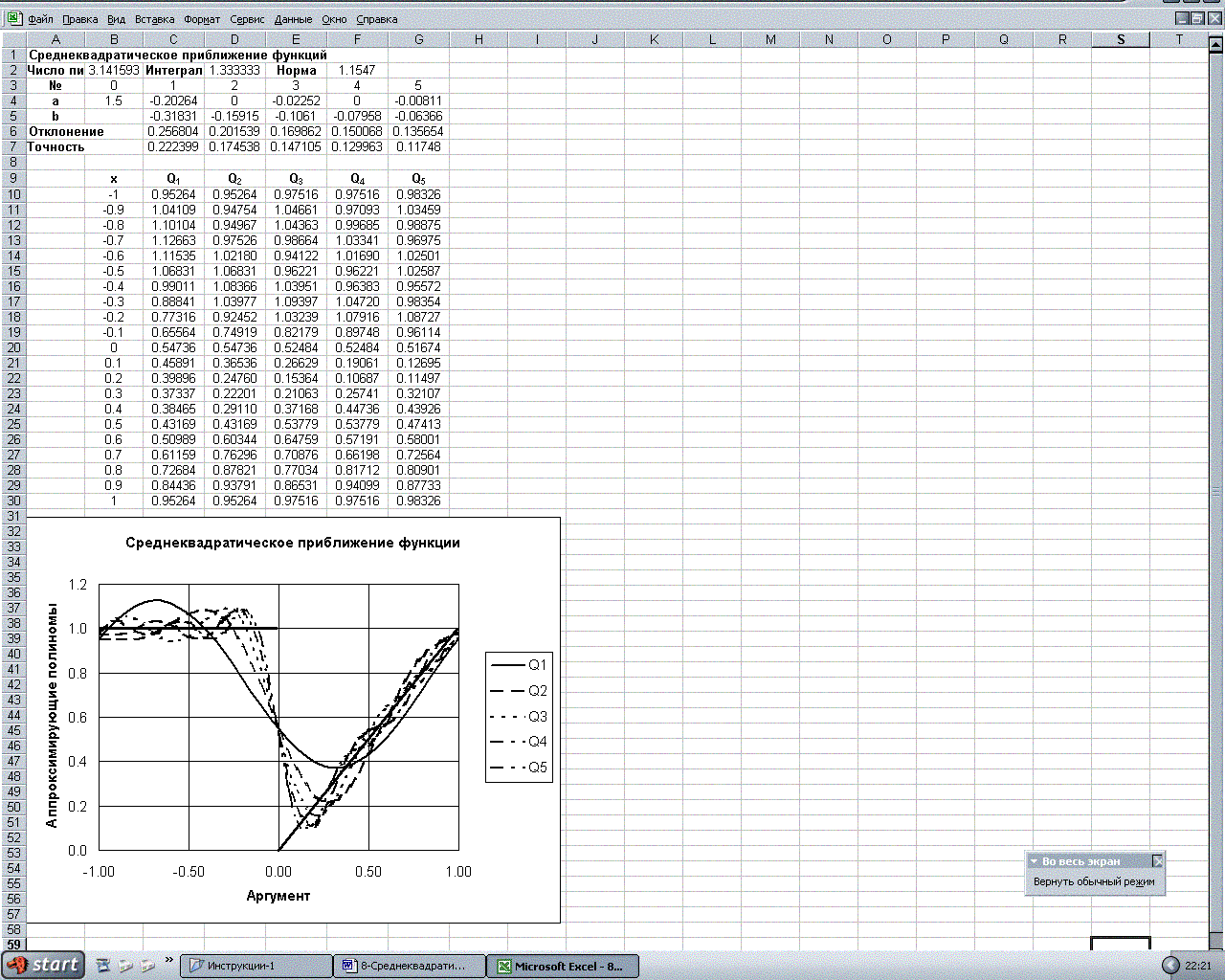
Вид расчетного листа MS Exсel для примера 2.
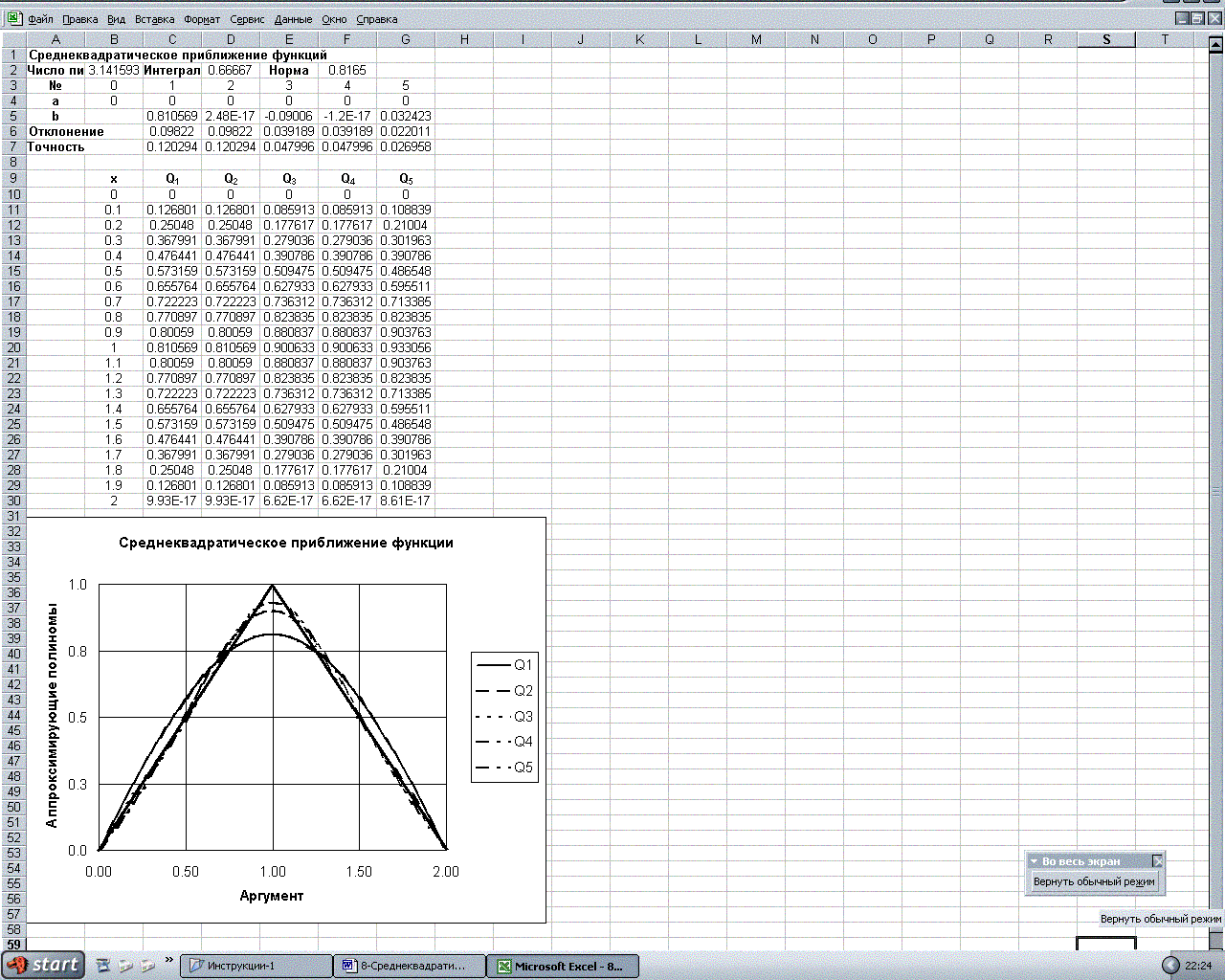
Лабораторная работа № 9
"Точечное среднеквадратичное приближение функций"
Элементы теории.
Пусть на множестве точек xi , i = 1, 2, … , m задана функция f(x) и определена система функций gk(x), k = 1, 2, … . Скалярным произведением функций gk(x) и gl(x) на множестве точек xi , i = 1, 2, … , m называется сумма произведений значений функций, вычисленных во всех точках, то есть
![]() .
(1)
.
(1)
Число
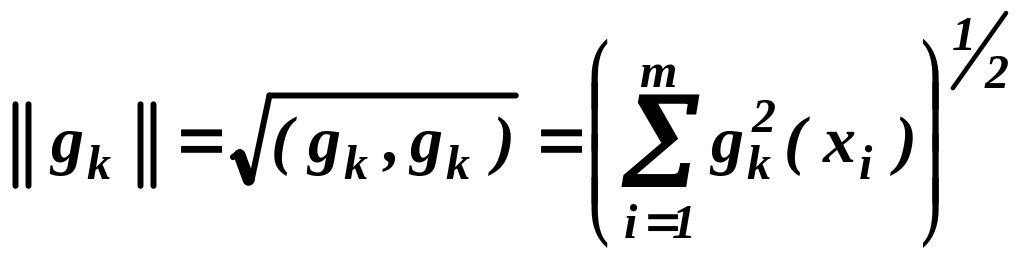 является нормой функции gk(x)
на множестве точек xi
, i
= 1, 2, … , m
.
является нормой функции gk(x)
на множестве точек xi
, i
= 1, 2, … , m
.
Функции gk(x) и gl(x) называются ортогональными на множестве точек, если их скалярное произведение на этом множестве равно нулю, то есть
![]() .
(2)
.
(2)
Система функций gk(x), k = 1, 2, … называется ортогональной xi , i = 1, 2, … , m , если все функции этой системы попарно ортогональны на этом множестве.
Коэффициенты C0 , C1 , … , Cn обобщенного многочлена
![]() (3)
(3)
называются коэффициентами Фурье функции f(x) относительно ортогональной системы функций, если они определяются по формулам
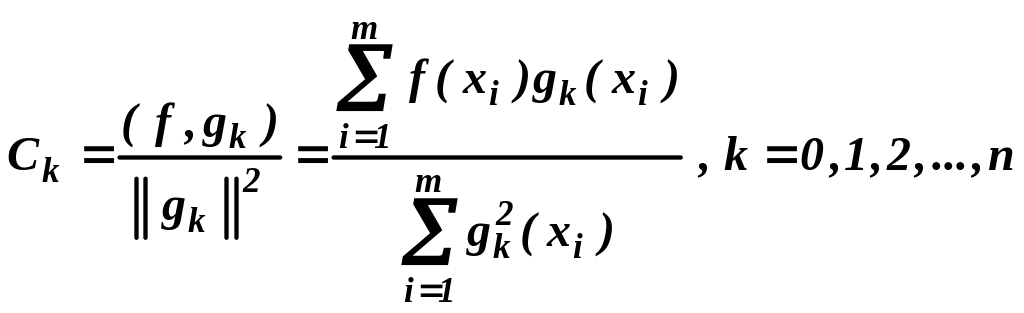 (4)
(4)
Теорема. Для функции f(x), определенной на множестве xi , i = 1, 2, … , m, обобщенный многочлен n-ой степени Qn(x) с коэффициентами Фурье относительно ортогональной на множестве точек системы функций gk(x) является многочленом наилучшего среднеквадратичного приближения этой функции, причем квадрат наименьшего среднеквадратичного отклонения определяется соотношением
![]() ,
(5)
,
(5)
где Сk – коэффициенты Фурье, определяемые по формулам (4).
Оценка погрешности приближения определяется величиной
![]() .
(6)
.
(6)
Многочленами
Чебышева на множестве точек xi
, i
= 1, 2, … , m
называются алгебраические многочлены,
ортогональные на этом множестве, с
нормой
![]() ,
отличной от нуля, и определяемые
следующими рекуррентными соотношениями:
,
отличной от нуля, и определяемые
следующими рекуррентными соотношениями:
![]() (7)
(7)
где
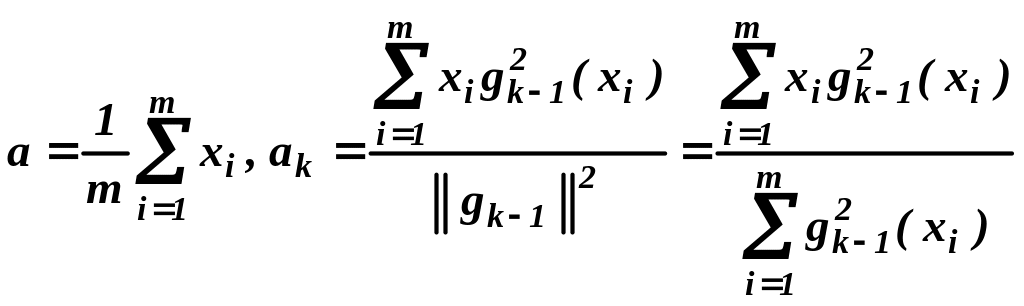 , (8)
, (8)
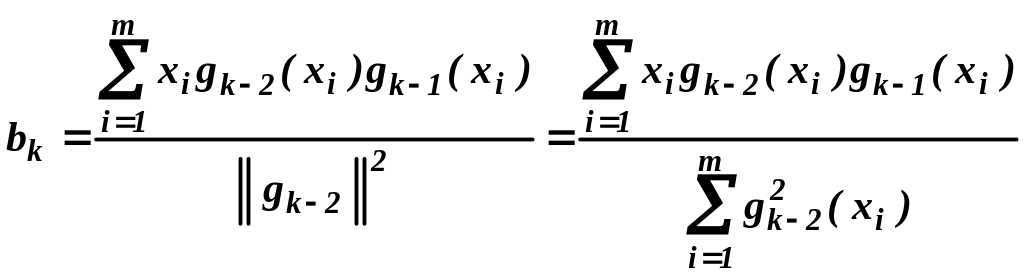 (9)
(9)
Многочлен gm( x ) степени m на множестве точек xi , i = 1, 2, … , m, полученный по рекуррентным формулам (7)-(9), на этом множестве имеет норму, равную нулю, и не является многочленом Чебышева.
