
- •Работа №7 исследование резонансных явлений в простых электрических цепях
- •7.1. Подготовка к работе
- •7.2. Экспериментальные исследования резонанса напряжений с применением моделирующих компьютерных программных средств Multisim.
- •Вопрос 1. Как, используя эквивалентные схемы цепи для , и , определить значения на этих частотах и проконтролировать результаты эксперимента? Приведите схемы замещения для этих частот.
- •Вопрос 2. В чем сходство и в чем различие данных, измеренных и рассчитанных в 7.2.1 и 7.2.2?
- •Вопрос 3. В чем сходство и в чем различие данных 7.2.2 и 7.2.3? Почему диапазон изменения частоты другой?
- •7.3. Исследование резонанса токов и ачх параллельного контура
- •Вопрос 4. Как, используя эквивалентные схемы цепи для и определить значения ачх на этих частотах и проконтролировать результаты эксперимента?
- •7.3.2. Исследование резонанса токов и ачх контура с большими потерями
- •Вопрос 5. В чем сходство и в чем различие данных, измеренных и рассчитанных в 7.3.1 и 7.3.2?
- •7.3.3. Исследование влияния изменения емкости на характеристики контура.
- •Вопрос 6. В чем сходство и в чем различие данных 7.3.2 и 7.3.3? Почему диапазон изменения частоты иной?
- •7.4. Требования к отчету
Работа №7 исследование резонансных явлений в простых электрических цепях
Соответствует работе № 7 классической лаборатории цепей [1].
7.1. Подготовка к работе
Цель работы: исследование резонанса и амплитудно-частотных характеристик (АЧХ) последовательного и параллельного колебательных контуров.
Резонанс
– такое состояние
![]() -цепи
в установившемся синусоидальном режиме,
при котором напряжение и ток цепи
совпадают по фазе.
-цепи
в установившемся синусоидальном режиме,
при котором напряжение и ток цепи
совпадают по фазе.
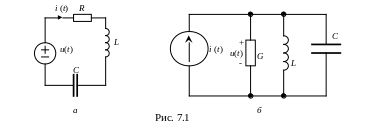
Схемы исследуемых цепей приведены на рис. 7.1. Резонанс в цепи рис. 7.1, а называют резонансом напряжений, а цепь – последовательным контуром; резонанс в цепи рис. 7.1, б – резонансом токов, а цепь – параллельным контуром. При резонансе вещественными становятся комплексное сопротивление последовательной цепи
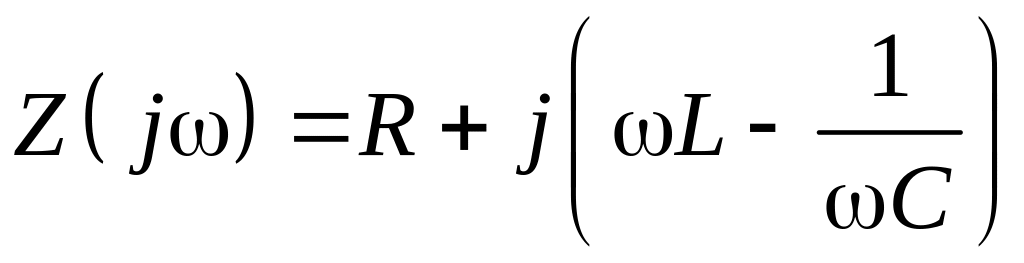
и, соответственно, комплексная проводимость параллельной цепи
![]()
Отсюда резонансная частота приведенных на рис. 7.1, а, б цепей:
![]() (7.1)
(7.1)
При резонансе модуль проводимости цепи на рис. 7.1, а становится максимальным:
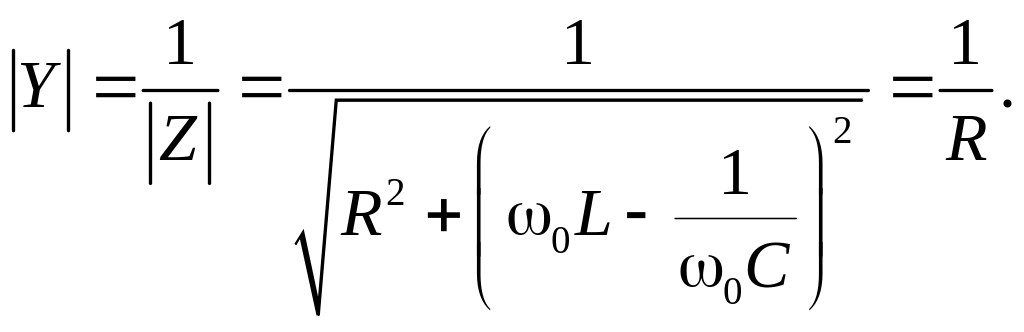 (7.2)
(7.2)
Это
значит, что при
![]() максимальным будет ток:
максимальным будет ток:
![]() (7.3)
(7.3)
Напряжения
на емкости и индуктивности в цепи на
рис. 7.1, а при резонансе компенсируют
друг друга и могут быть во много раз
больше напряжения источника. Отношение
действующего значения напряжения любого
из реактивных элементов к напряжению
источника при
называют добротностью
![]() последовательного контура:
последовательного контура:
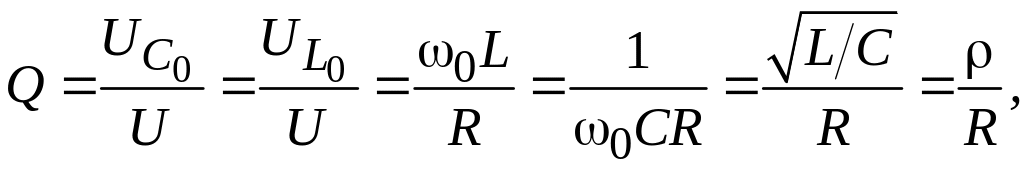 (7.4)
(7.4)
где
![]() – характеристическое сопротивление
контура.
– характеристическое сопротивление
контура.
Если
в режиме резонанса измерены напряжения
на входе
![]() и на емкости
и на емкости
![]() ,
ток
,
ток
![]() и резонансная частота
и резонансная частота
![]() ,
то из приведенных соотношений можно
определить все параметры последовательного
контура: сопротивление
,
то из приведенных соотношений можно
определить все параметры последовательного
контура: сопротивление
![]() из (7.3), добротность
и характеристическое сопротивление
из (7.4), а емкость и индуктивность из
(7.1) и (7,4):
из (7.3), добротность
и характеристическое сопротивление
из (7.4), а емкость и индуктивность из
(7.1) и (7,4):
![]() (7.5)
(7.5)
Параллельный -контур на рис. 7.1, б дуален последовательному. При резонансе токов максимальным становится модуль его комплексного сопротивления:
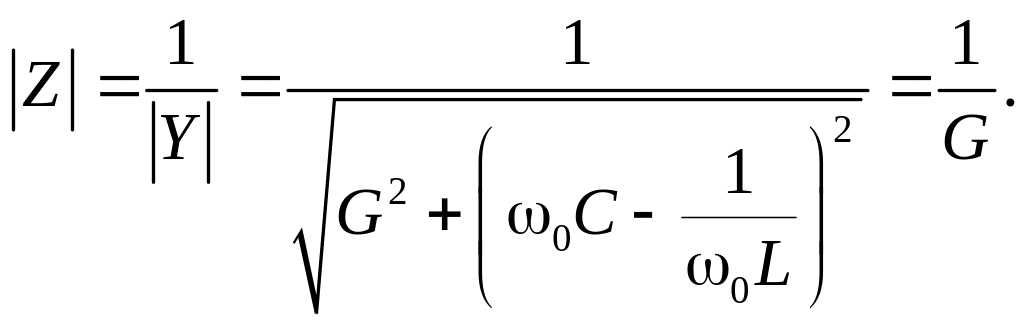 (7.6)
(7.6)
Это значит, что при максимальным будет напряжение на входе цепи:
![]() (7.7)
(7.7)
Токи, протекающие через индуктивность и емкость в цепи на рис. 7.1, б, при резонансе компенсируют друг друга и могут во много раз быть больше тока источника. Отношение действующего значения тока любого из реактивных элементов к току источника при называют добротностью параллельного контура:
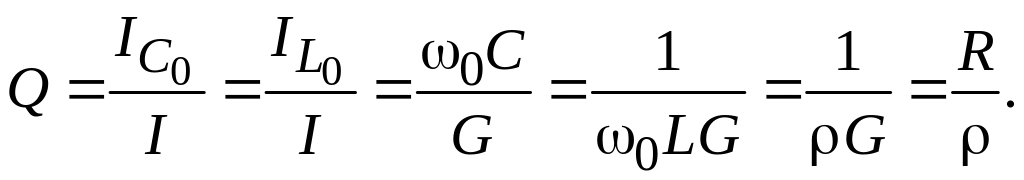 (7.8)
(7.8)
Если
в режиме резонанса измерены входной
ток
![]() и ток емкости
и ток емкости
![]() ,
напряжение
,
напряжение
![]() и резонансная частота
,
то из (7.7) можно определить
и резонансная частота
,
то из (7.7) можно определить
![]() ,
из (7.8) –
и
,
а из (7.5) –
,
из (7.8) –
и
,
а из (7.5) –
![]() и
и
![]() .
.
При отклонении частоты от резонансной реактивное сопротивление последовательного контура и реактивная проводимость параллельного не равны нулю, поэтому ток первого и напряжение второго уменьшаются.
Амплитудно-частотная характеристика (резонансная кривая) последовательного контура есть зависимость модуля проводимости (7.2) от частоты:
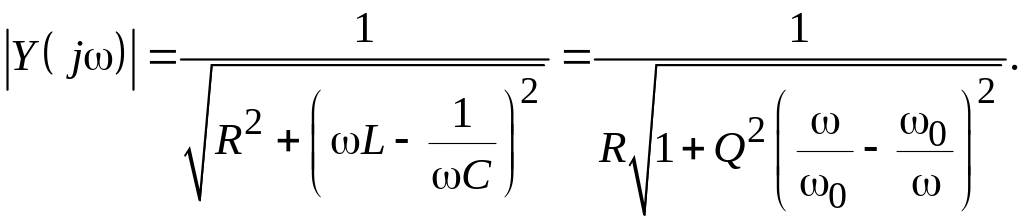 (7.9)
(7.9)
Для параллельного контура, дуально, АЧХ – это зависимость модуля сопротивления (7.6) от частоты:
 .
(7.10)
.
(7.10)
П
f
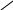
![]() представлен на рис. 7.2.
представлен на рис. 7.2.
“Острота”
резонансной кривой определяет частотную
избирательность цепи. По АЧХ можно
определить добротность контура. Она
равна отношению
к полосе пропускания
![]() ,
измеренной по уровню 0,707 от максимума
АЧХ:
,
измеренной по уровню 0,707 от максимума
АЧХ:
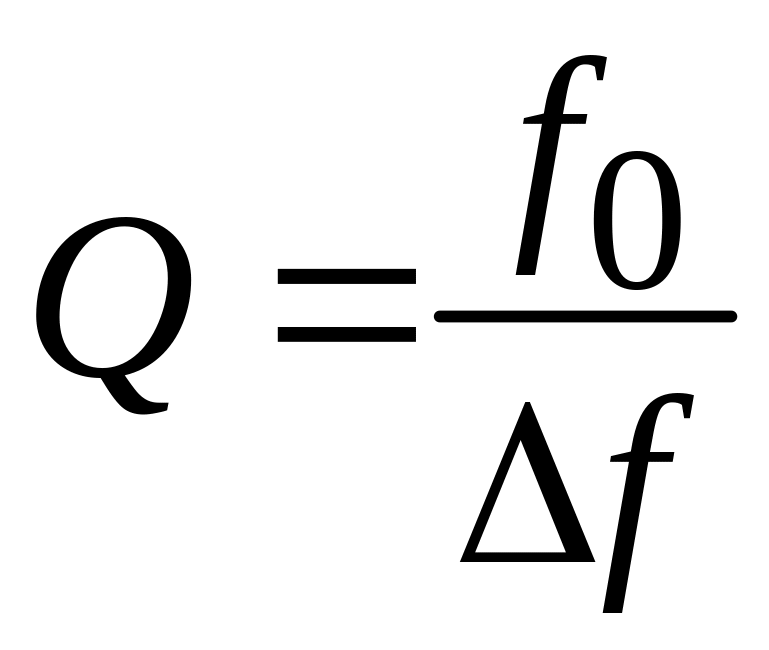 .
(7.11)
.
(7.11)
