Методические указания к решению задания:
1. Рассмотрим экономико-математическую модель зависимости суммы прибыли от объёма выручки от реализации, которая выражается линейным уравнением вида:
Y = a0 + a1X ,
где Y - прибыль, руб.;
X - выручка, руб.;
a0, a1 - параметры уравнения;
a1 - коэффициент регрессии, показывающий, на сколько рублей увеличивается прибыль при увеличении выручки на один рубль;
a0 - сумма прибыли, определяемая совокупным действием всех других факторов, кроме выручки, руб.
Решение модели заключается в нахождении параметров a0 и a1, которые обычно отыскиваются методом наименьших квадратов из системы нормальных уравнений:
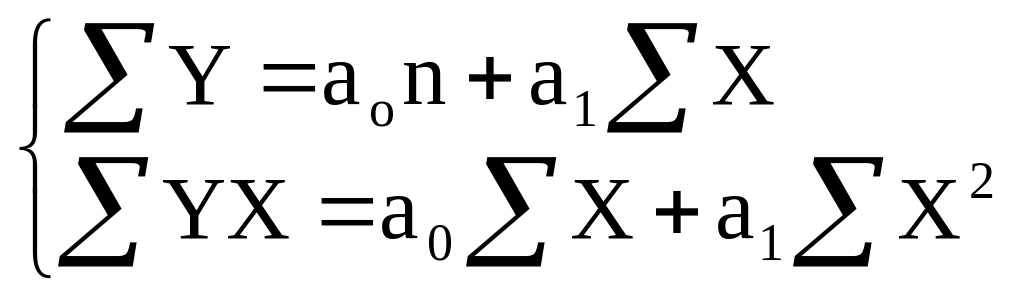
Важное значение для обоснованности модели имеет её репрезентативность. Репрезентативность наблюдений - показательность наблюдений, т. е. соответствие характеристик, полученных в результате частичного исследования объекта, характеристикам этого объекта в целом. Репрезентативность полученных показателей модели проверяется путём расчётов среднего квадратического отклонения полученных данных от фактических и коэффициента вариации.
Среднее квадратичное отклонение определяется по формуле:
,
где G – среднее квадратичное отклонение;
Y – фактическая сумма прибыли, руб.;
Yx – расчётная сумма прибыли, руб.;
n – число случаев наблюдения.
Коэффициент
вариации определяется по формуле:
,
где V – коэффициент вариации, %;
G – среднее квадратичное отклонение, руб.;
– среднеарифметическая
величина прибыли, руб.
2. Для удобства расчетов их можно представить в виде таблицы 4.
Таблица 4
Квартал |
Прибыль фактическая, Y |
Выручка от реализации, X |
YX |
X2 |
Прибыль расчетная, Yx |
Y-Yx |
(Y-Yx)2 |
I |
5,1 |
21 |
107.1 |
441 |
5.05 |
0.05 |
0.0025 |
II |
4,8 |
20 |
96 |
400 |
4.85 |
-0.05 |
0.0025 |
III |
4,6 |
19 |
87.4 |
361 |
4.65 |
-0.05 |
0.0025 |
IV |
4,5 |
18 |
81 |
324 |
4.45 |
0.05 |
0.0025 |
|
19 |
78 |
371.5 |
1526 |
19 |
0 |
0.01 |
3. Последовательность расчётов:
3.1 Находятся параметры линейного уравнения зависимости Y от X решением системы нормальных уравнений, и определяется общий вид зависимости Y от X.
Воспользуемся методом наименьших квадратов :
Составим систему уравнений:
19=
4*
+
78*
371.5=78 * + 1526 *
Решение:
=0.85
=0.2
3.2 В полученное уравнение зависимости Y от X подставляются значения X по кварталам текущего года и рассчитываются значения Yx (расчётная прибыль), а также их отклонения и квадраты этих отклонений по кварталам текущего года.
Полученное уравнение:
у = 0.85 + 0.2*х (1)
где параметр а1 = 0,2 показывает, что при увеличении выручки на 1 руб. прибыль возрастает на 0,2 руб.; параметр а0 = 0.85 показывает среднюю сумму прибыли (0.85 млн. руб.), которая определяется действиями всех других факторов, кроме выручки.
Подставив значения X (Выручка от реализации) в уравнение ( 1) , получим Прибыль расчетную, Yx (Табл.1):
у = 0.85 + 0.2*21=5.05
Рассчитаем отклонения:
Y-Yx = 5.1- 5.05=0.05
Квадраты отклонений :
(Y-Yx)2 = (0.05 ) ^2=0.0025
Проверим репрезентативность полученной модели путём расчётов среднего квадратического отклонения полученных данных от фактических и коэффициента вариации..
-среднее
квадратичное отклонение
G=
=
0.05
-
Коэффициент вариации
V=
(0.05/ 4.75)*100%=1.05%
3.3 Оценивается значимость полученных величин G и V, исходя из того, что значение G - должно существовать, а V не должно превышать 6 %
4. На основании полученных результатов делается вывод о возможности использования данной модели при планировании прибыли, и при положительном ответе составляется план по прибыли на I квартал следующего года.
Вывод:
Данная модель является репрезентативной , так как коэффициент V=1.05%<6%, Коэффициент вариации показывает, что степень отклонения расчетных показателей от фактических составляет всего лишь 1.05%, т. е. незначительная. Поэтому можно сделать вывод о возможности использования данной модели при планировании прибыли.
План по прибыли на I квартал следующего года:
Yпланов.= 0.85+ 0.2 * 33= 7.45 млн. руб.