Алгоритм максимизации ожидания (EM) отдельным модулем / ЛНГР_часть5_испр_2

2.4 Описание базовых алгоритмов

Ниже приводится подробное описание алгоритмов, рекомендуемых для включения в состав программного обеспечения пакета программ интеллектуального анализа БД.

2.4.3 Стандартный алгоритм максимизации ожидания (Expectation Maximization -EM)

Алгоритм EM [25] лежит в основе достаточно эффективной процедуры поиска кластеров, основанной на приближении обучающей выборки смесью нормальных распределений. При этом количество используемых в смеси нормальных распределений однозначно соответствует количеству кластеров. В таком случае процедура поиска кластеров полностью аналогична методу итеративной оценки параметров распределения. Алгоритм EM представляет собой итеративный метод оценки неизвестных параметров с использованием данных наблюдения . При этом нам не известны значения некоторых «побочных» переменных В частном случае задача может быть поставлена следующим образом:

. (99)

Идея алгоритма проста: поочерёдно оценивать и Следует заметить, что вместо поиска наилучшего для данной оценки на каждой итерации в EM используется распределение в пространстве .

Реализация алгоритма EM. Рассмотрим набор величин и базовые соотношения, которые используются в алгоритме EM. Пусть задана обучающая выборка

, (100)

где каждый вектор представлен совокупностью значений признаков

. (101)

Задача кластер-анализа в данном случае заключается в построении вероятностной модели обучающей выборки, где для каждого вектора обучающей выборки можно вычислить выходной вектор

, (102)

каждая компонента которого определяет (апостериорную) вероятность принадлежности данного вектора обучающей выборки кластеру . Во всех практических применениях алгоритма EM модель представляет собой смесь k m-мерных нормальных распределений, т.е.

, (103)

где значения математических ожиданий и СКО и представляют собой искомое множество параметров модели, а - константа нормализации.

Критерий оптимальности параметров модели представляет собой функцию логарифмического правдоподобия (log-likelihood). Определим набор весов вектора обучающей выборки на каждом шаге работы алгоритма как

, (104)

где и соответственно априорные и апостериорные вероятности принадлежности вектора к кластеру.

Тогда логарифмическое правдоподобие модели для каждого вектора обучающей выборки на каждом шаге алгоритма вычисляется из следующего соотношения:

. (105)

Практически используется усредненное по обучающей выборке логарифмическое правдоподобие

. (106)

Критерием остановки алгоритма служит выражение

, (107)

где - среднее логарифмическое правдоподобие на итерации алгоритма;

-некоторая малая величина (типичное значение ).

По выполнению условия (107) алгоритм останавливается и текущие значения параметров модели считаются оптимальными.

Алгоритм EM определяется как последовательное выполнение шагов E и M. Приведём упрощённое описание алгоритма.

На шаге E производится оценка текущих вероятностей принадлежности векторов обучающей выборки к кластерам. Выполняется последовательность действий :

1. для каждого вектора обучающей выборки вычисляется вероятность принадлежности к кластеру 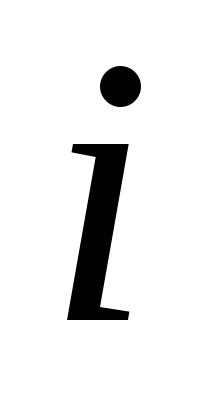при помощи выражения (103);

2) производится пересчёт весов всех векторов обучающей выборки согласно выражению (104);

3. для каждого вектора обучающей выборки вычисляется логарифмическое правдоподобие (105); усредненное его значение (106) используется далее в алгоритме;

4. производится пересчёт априорных вероятностей по формуле

. (108)

На шаге M производится перерасчёт параметров модели в два этапа:

1. для всех кластеров по всем атрибутамвыполняется предварительный расчёт параметров модели:

, (109)

, (110)

; (111)

2. по всем атрибутам для всех кластеров производится окончательный расчёт параметров модели по результатам предварительных вычислений (109), (110), (111):

, (112)

, (113)

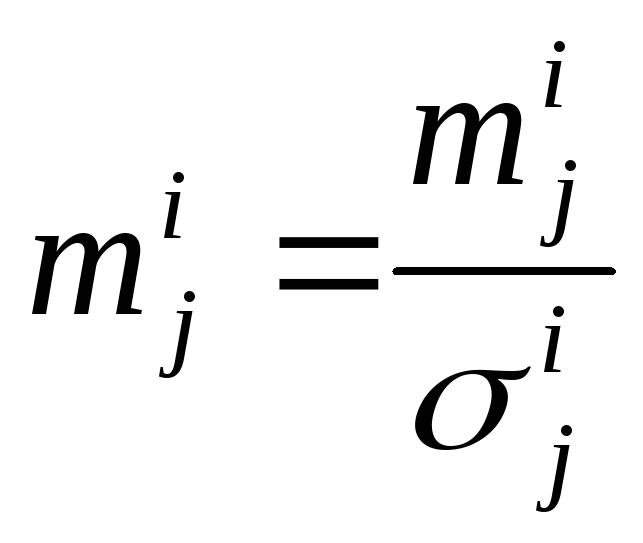. (114)

Выполнение шагов E и M производится по следующему алгоритму:

1. задание случайных начальных параметров модели;

2. выполнение шага M;

3. выполнение шага E;

4. если выполнено условие (107), то алгоритм завершает работу, иначе переход к перечислению 2.