Перетворення Галілея для координат і швидкостей.

Видатний італійський учений Г.Галілей (XVI – XVII ст.) встановив формули переходу координат матеріальної точки М(x,y,z) й часу t, заданих в одній інерціальній СВ до координат x',y',z' й часу t' в іншій ІСВ. Аналогічні формули переходу Г.Галілей встановив і для швидкостей.

Формули, що взаємопов’язують координати і швидкості матеріальної точки в двох різних інерціальних СВ, називаються перетвореннями Галілея.

Для простоти міркувань Г.Галілей одну систему відліку К вибрав умовно нерухомою (основною СВ), а іншу К' – рухомою, що рівномірно і поступально переміщується відносно К вздовж осі OX (рис. 1.7).

Рис. 1.7.

З OO'M':

(*)

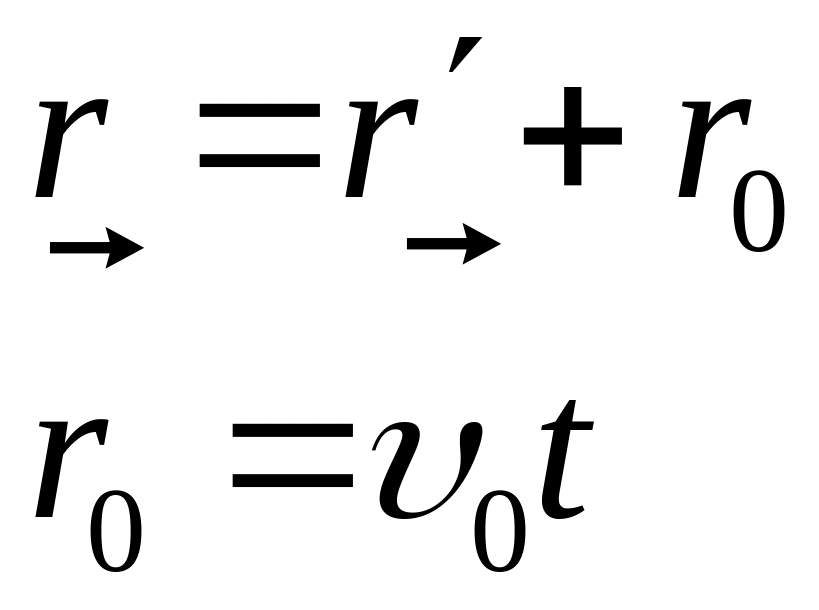
Проектуючи вектори, що входять в отримане рівняння, маємо формули, які носять назву перетворень Галілея для координат.

(1-13)

Продиференціюємо (*) за часом ; Отримаємо вираз (1-13а) має назву перетворення Галілея для швидкостей

(1-13а)

Перетворення Галілея для швидкостей носить назву класичного закону додавання швидкостей.

Швидкість точки (тіла) відносно нерухомої СВ дорівнює векторній сумі 2 швидкостей: швидкості точки відносно рухомої СВ і швидкості цієї рухомої СВ відносно нерухомої.

Висновок: координати і швидкості точки (тіла) при переході від однієї інерційної СВ до іншої змінюються; час руху залишається величиною незмінною або інваріантною.

Принцип незалежності рухів.

В загальному випадку одна і та ж матеріальна точка (тіло) може перебувати одночасно в 2 або більше рухах. Тоді має місце висновок, зроблений Г.Галілеєм на основі експерименту і називається принципом незалежності рухів: Якщо тіло (матеріальна точка) одночасно перебуває в 2 або більше рухах, то ці окремі рухи не впливають один на інший, а всі величини, що характеризують ці рухи додаються як незалежні.

Таким чином, будь-який механічний рух можна розглядати, як складний процес, який можна представити, як суму 2 незалежних рухів, тобто будь-який механічний рух можна розкласти на декілька більш простих рухів, а це значно спрощую розв’язок механічних задач.

Приклад (рис. 1.8.): а) рух тіла, кинутого горизонтально;

б) рух тіла, кинутого під кутом до горизонту.

Рис. 1.8.