Кінематика найпростіших механічних рухів.

До найпростіших механічних рухів точки відносяться рівномірний і рівноприскорений прямолінійні рухи.

Рівномірний прямолінійний рух – рух, при якому величина і напрям вектора швидкості з часом не змінюються, називається рівномірним і прямолінійним, тобто

тоді векторне рівняння рівномірного руху матиме вигляд:

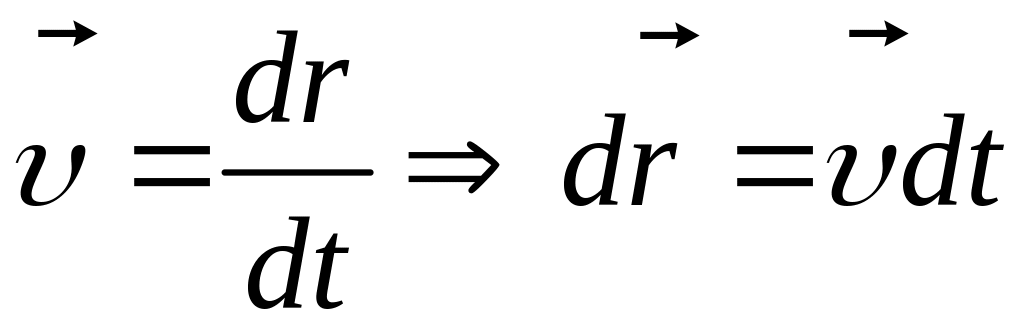
Межі інтегрування знаходимо із початкових умов.

Нехай при ; ;

;

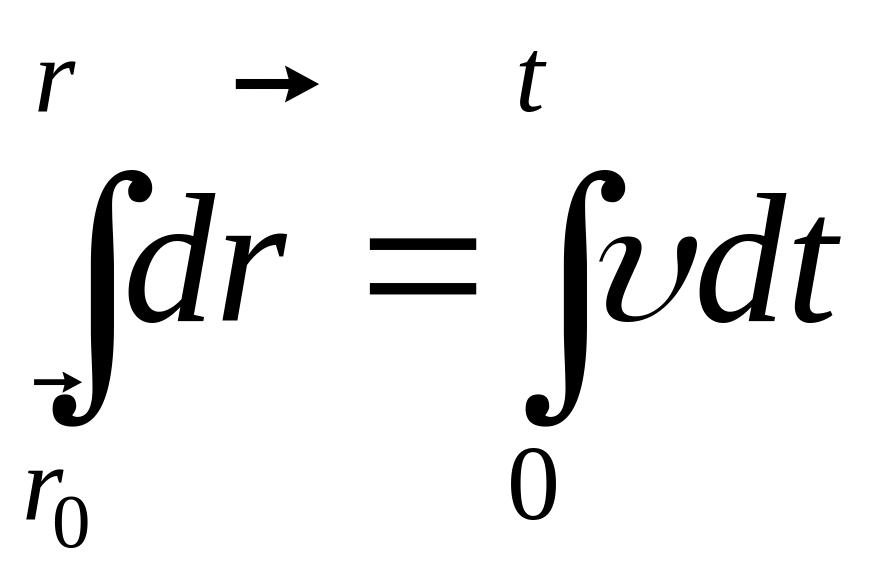
виражає закон прямолінійного рівномірного руху.

Формулювання:

Радіус-вектор матеріальної точки при рівномірному прямолінійному русі змінюється з часом згідно лінійного закону.

Закон рівномірного руху в координатній формі:

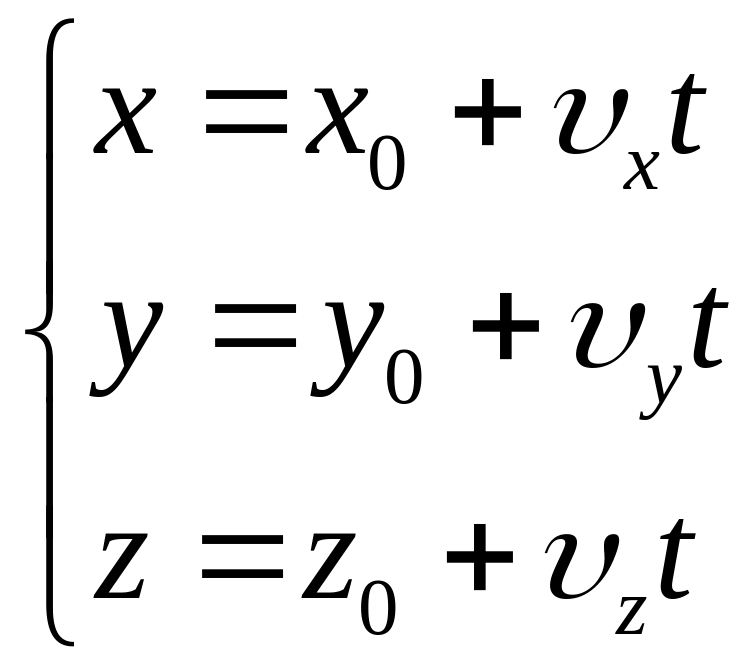(1-8)

Пройдений шлях визначається за формулами:

(1-8а)

З мал. 1 маємо:

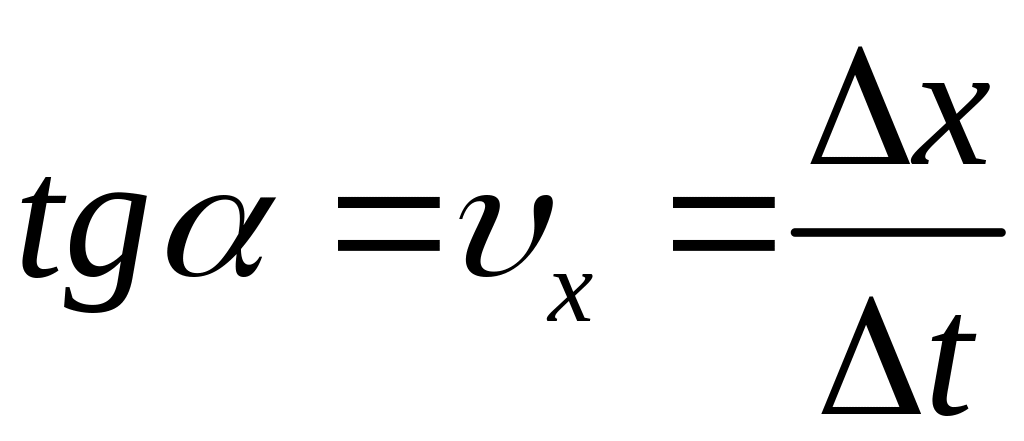
Демонстрація рівномірного прямолінійного руху за допомогою візка з капельницею.

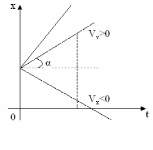
Графік рівномірного руху:

Є промінь з вершиною, що відповідає початку руху (рис. 1)

Рис. 1.4.

Рівнозмінний прямолінійний рух – це рух з постійним вектором прискорення.

, якщо – для рівноприскореного руху

– для рівносповіль-неного руху.

;

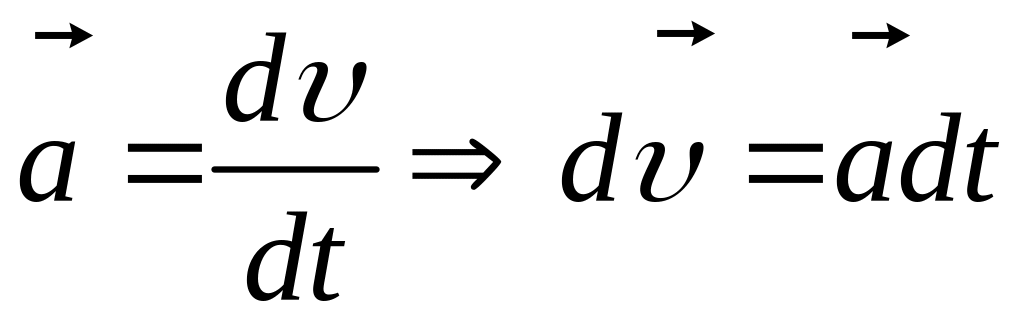При ;

;

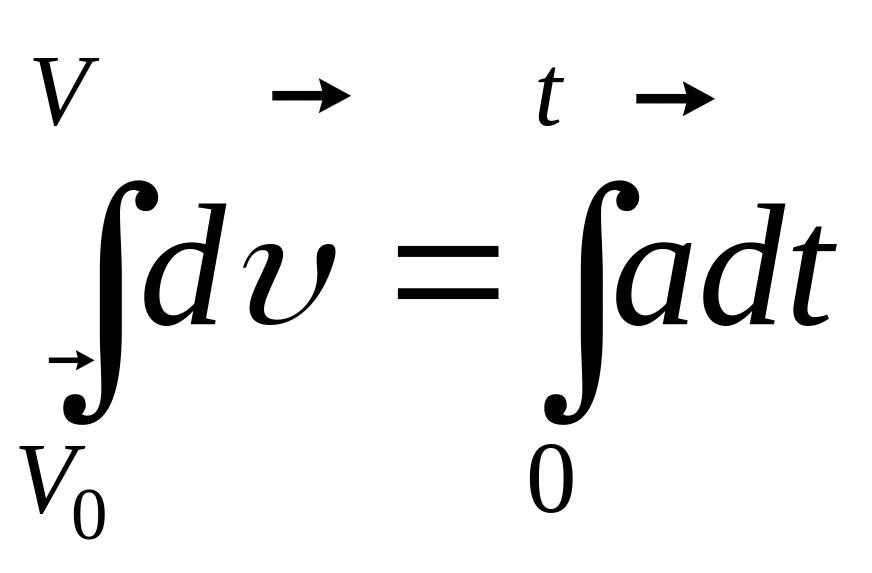(1-9)

Вектор швидкості при рівно змінному русі змінюється з часом за лінійним законом в координатній формі:

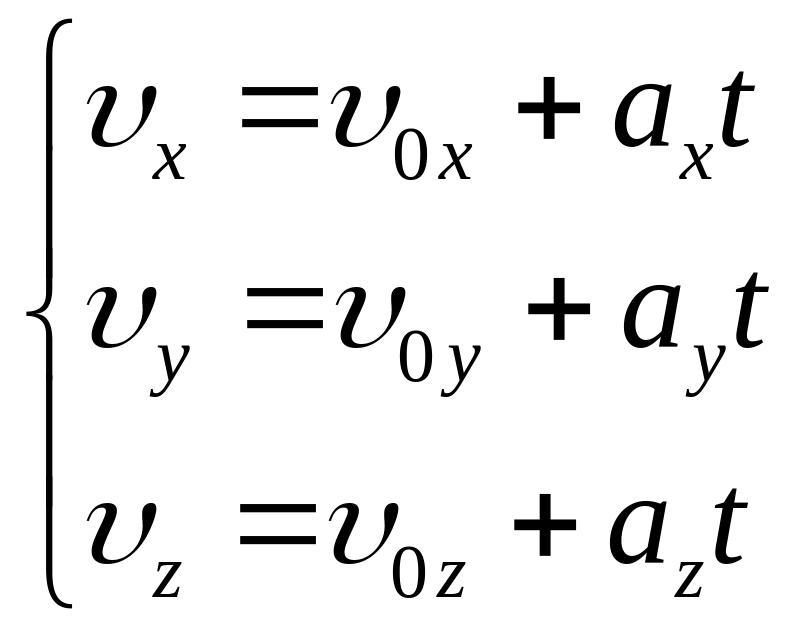(1-9а)

Ортогональні проекції швидкості при рівнозмінному русі змінюється з часом згідно лінійного закону.

Знайдемо закон рівнозмінного прямолінійного руху

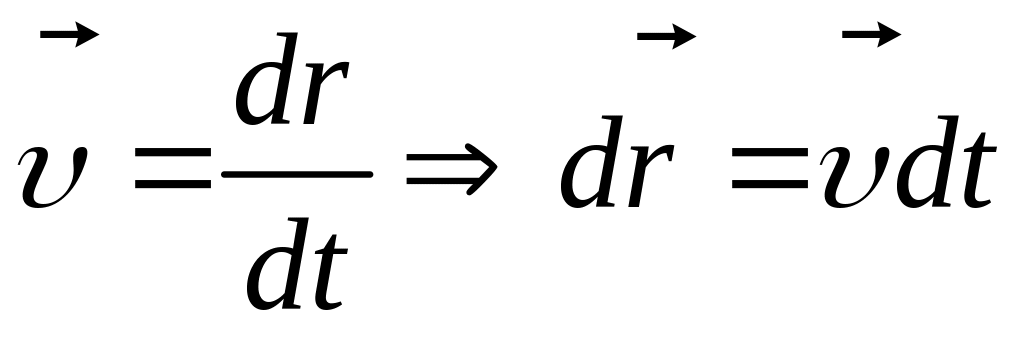
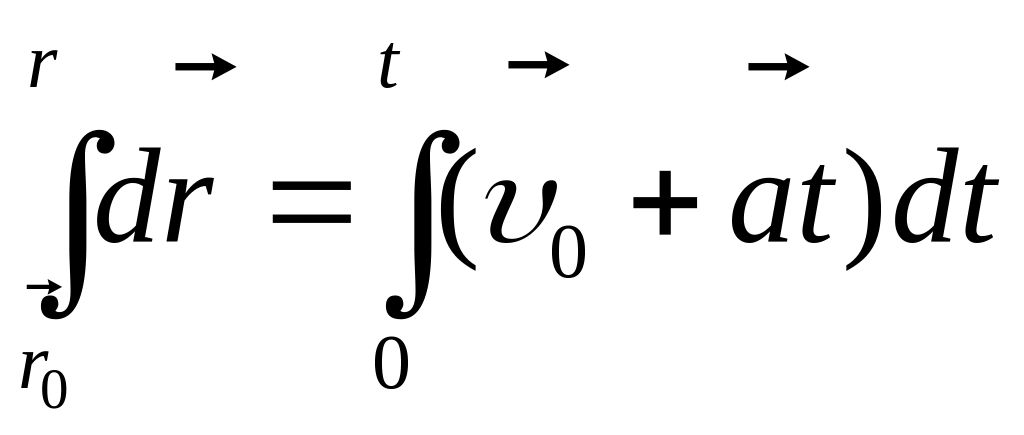
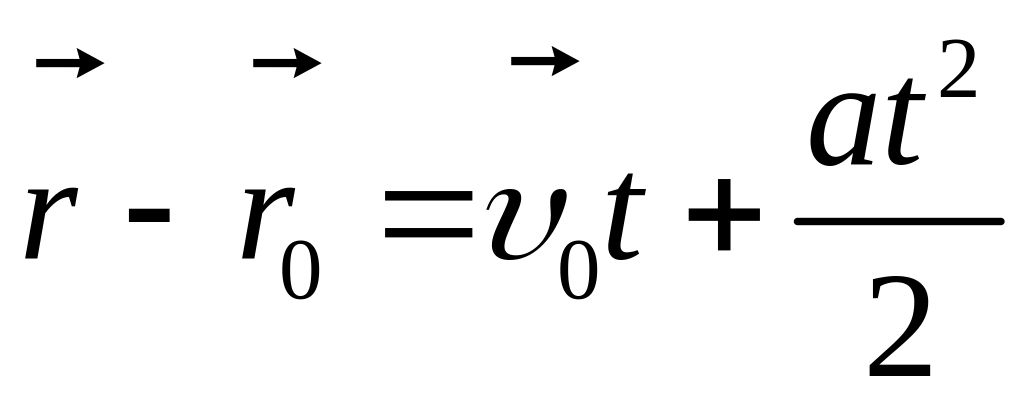
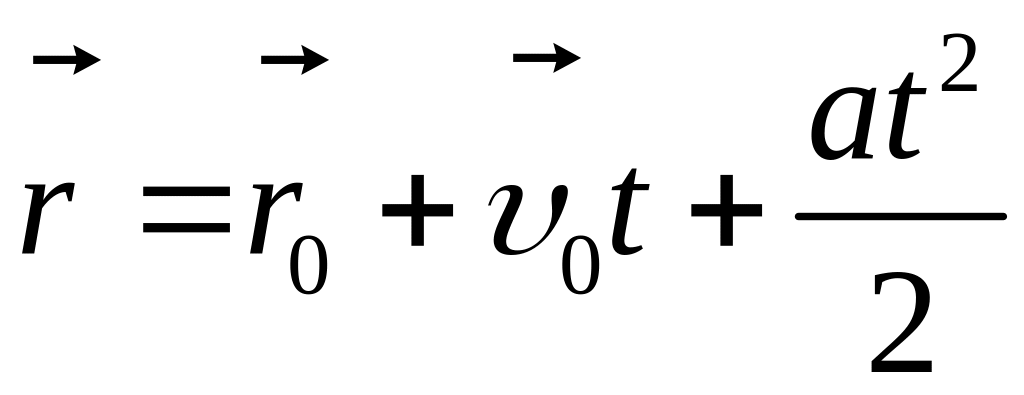(1-10)

Отримане рівняння описує закон руху у векторній формі

Формулювання: Радіус-вектор точки при рівнозмінному русі змінюється з часом за квадратичним законом.

Кінематичні рівняння рівнозмінного руху в координатній формі мають вигляд:

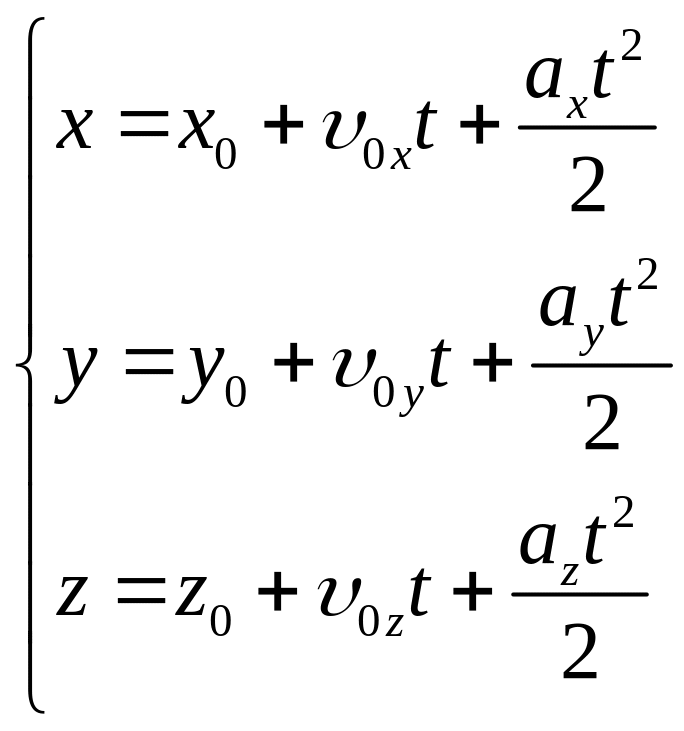(1-10а)

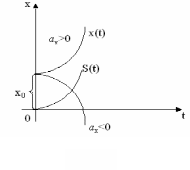
Координати матеріальної точки (її радіус-вектор) при рівнозмінному русі змінюються з часом за квадратичним (параболічним) законом.

Рис. 1.5.

Графік рівнозмінного руху має вигляд:

Вільне падіння – окремий випадок рівноприскореного прямолінійного руху.

Вільне падіння – це рух із стану спокою в безповітряному просторі (тобто, коли опором повітря нехтують).

Можна показати, що шляхи, які проходить матеріальна точка в прямолінійному рівноприскореному русі без початкової швидкості (вільне падіння) за послідовні рівні проміжки часу відносяться, як натуральний ряд непарних чисел. S₁ : S₂ : S₃ : …= 1 : 3 : 5 : …

Демонстрація рівноприскореного прямолінійного руху за допомогою візка з капельницею або демонстрація вільного падіння краплин води за допомогою стробоскопа.

Відносність механічного руху – одна з основних властивостей руху, що випливає з його означення.

Відносність механічного руху – означає, що рух одного і того ж тіла (точки), що розглядається відносно різних системи (СВ) відліку може мати різний характер, а його кінематичні параметри ( ) (характеристики) змінюються при переході від однієї системи відліку до іншої.

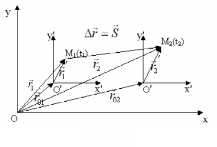
Зручно розглядати механічний рух відносно двох систем відліку.

а) СВ, умовно прийнятої за нерухому, вона називається основною;

б) рухомої СВ, що зв’язана з рухомим тілом.

Рис. 1.6.

Нехай в момент часу t₁:

t₁: т. М₁ – ; ;

t₂: т. М₂ – ; ;

За умови, що рухома CВ ( ) здійснює поступальний рух відносно нерухомої CВ (ОХY)

а) Визначимо вектор переміщення

;

;

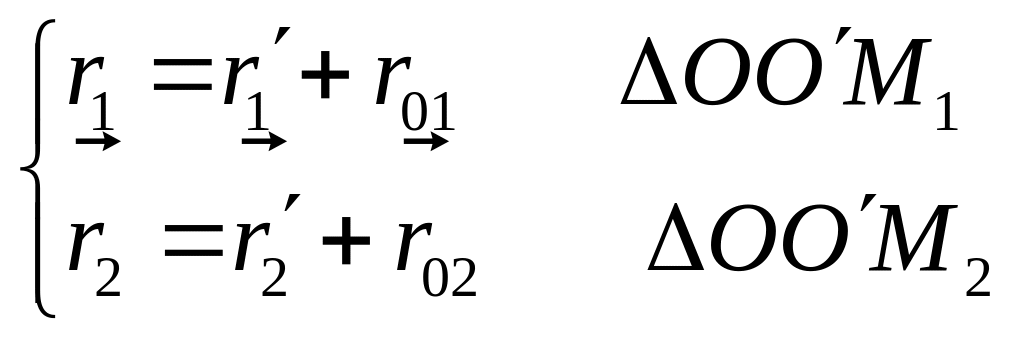
Тоді маємо: або

(1-11)

Висновок:

Вектор переміщення матеріальної точки відносно СВ, умовно прийнятої за нерухому, дорівнює векторній сумі 2 переміщень: переміщення точки відносно рухомої СВ і переміщення рухомої СВ відносно нерухомої.

б) Визначимо вектор швидкості .

Розділимо почленно (1) на проміжки часу Δt, протягом якого відбувається рух і перейдемо до границі одержаного виразу за умови, що Δt → 0.

; ;

;



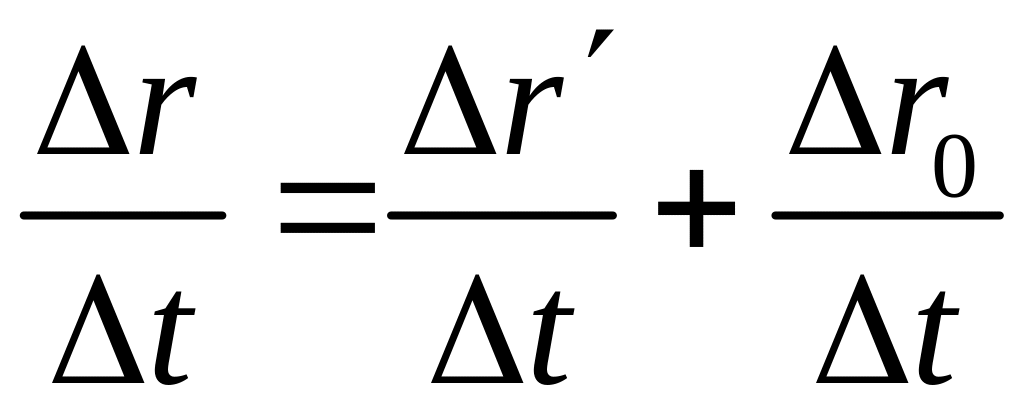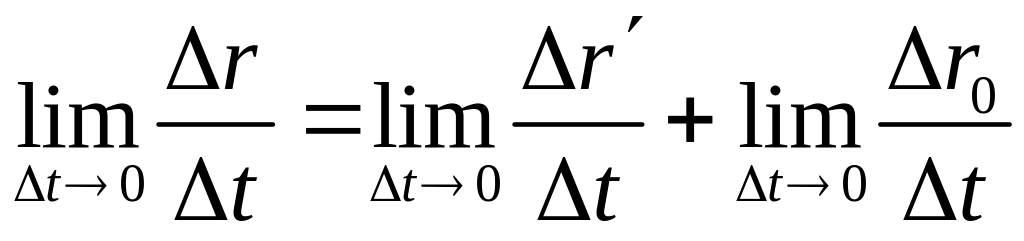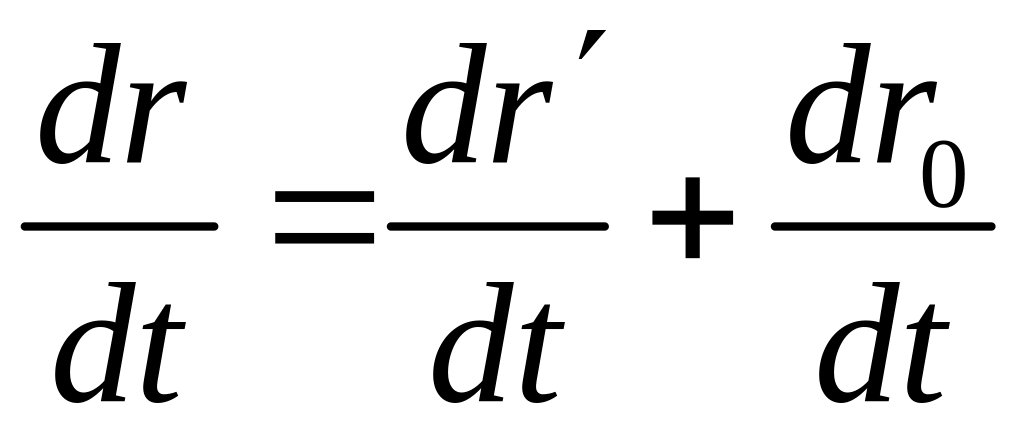
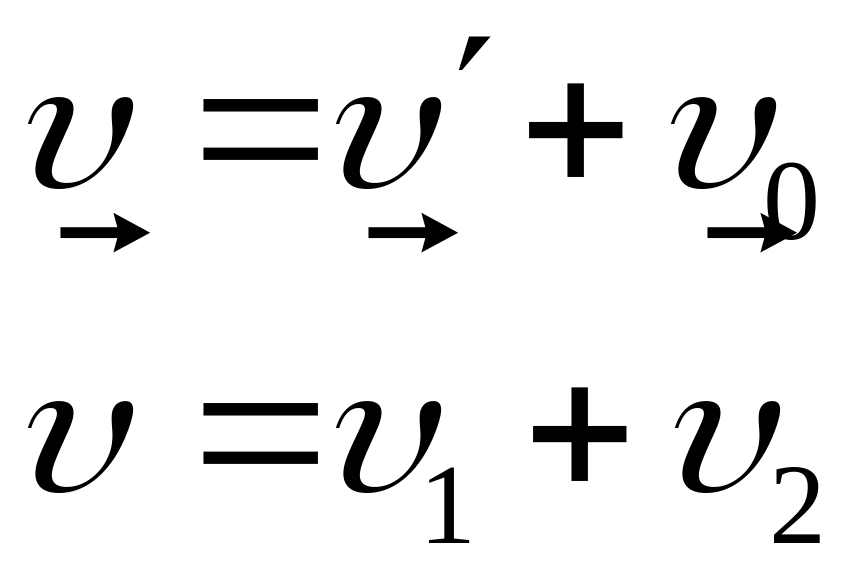(1-12)

Висновок: Швидкість тіла (точки) відносно нерухомої СВ, дорівнює векторній сумі 2 швидкостей: швидкості тіла (точки) відносно рухомої СВ і швидкості самої рухомої СВ відносно нерухомої.

Цей висновок носить назву класичного закону додавання швидкостей.

в) Визначимо, як змінюється прискорення при переході від однієї СВ до іншої. Знайдемо похідну за часом останнього виразу (формули додавання швидкостей):

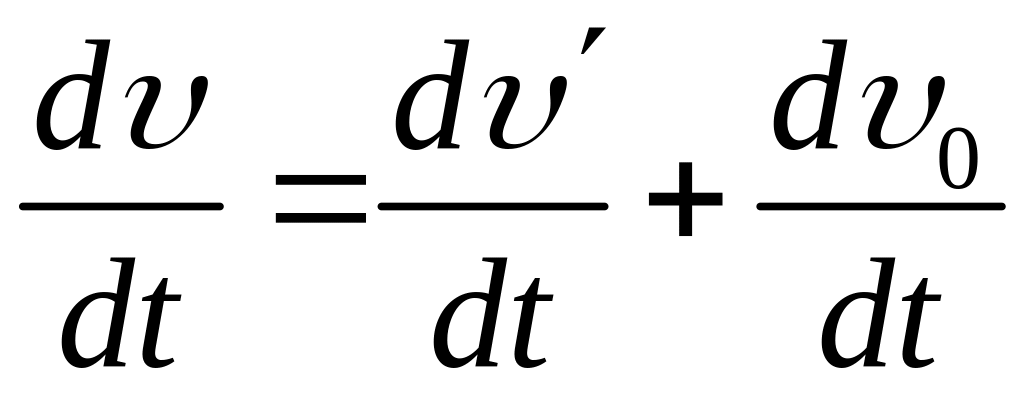
 або

(1-12а)

Висновок: У випадку нерівномірного поступального руху рухомої СВ, прискорення точки (тіла) відносно нерухомої СВ дорівнює векторній сумі 2 прискорень: прискорення точки (тіла) відносно рухомої СВ і прискорення самої рухомої СВ відносно нерухомої.

Якщо рухома СВ переміщається рівномірно прямолінійно, то  .

Тоді , тобто прискорення не змінюється при переході від нерухомої СВ до рухомої.

Цю часткову задачу вперше розглянув і розв’язав Г.Галілей, розглянувши інерціальні СВ, тобто СВ, що зв’язані з нерухомими тілами, або тілами, що рухаються рівномірно прямолінійно.

СВ, що переміщуються рівномірно і прямолінійно або знаходяться в стані спокою називаються інерціальними системами відліку.