Критические параметры

Критическими параметрами газа называются значения его макропараметров (давления, объёма и температуры) в критической точке, т.е. в таком состоянии, когда жидкая и газообразная фазы вещества неразличимы. Найдем эти параметры для газа Ван-дер-Ваальса, для чего преобразуем уравнение состояния:

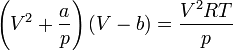
Мы получили уравнение третьей степени относительно .

В критической точке все три корня уравнения сливаются в один, поэтому предыдущее уравнение эквивалентно следующему:

Приравняв коэффициенты при соответствующих степенях , получим равенства:

Из них вычислим значения критических параметров...

...и критического коэффициента:

Приведённые параметры

Приведённые параметры определяются как отношения

Если подставить в уравнение Ван-дер-Ваальса получится приведённое уравнение состояния.

Стоит отметить, что если вещества обладают двумя одинаковыми приведёнными параметрами из трёх, то и третьи приведённые параметры у них совпадают.

Недостатки уравнения Ван-дер-Ваальса

1. Для реальных веществ

2. Для реальных веществ (скорее, )

3. Уравнение Ван-дер-Ваальса расходится с экспериментом в области двухфазных состояний.

Критическое состояние

Критическая точка — сочетание значений температуры и давления (или, что эквивалентно, молярного объёма ), при которых исчезает различие в свойствах жидкой и газообразной фаз вещества.

Критическая температура фазового перехода — значение температуры в критической точке. При температуре выше критической температуры газ невозможно сконденсировать ни при каком давлении.

В критической точке плотность жидкости и её насыщенного пара становятся равны, а поверхностное натяжение жидкости падает до нуля, потому исчезает граница раздела фаз жидкость-пар.

Для смеси веществ критическая температура не является постоянной величиной и может быть представлена пространственной кривой (зависящей от пропорции составляющих компонентов), крайними точками которой являются критические температуры чистых веществ — компонентов рассматриваемой смеси.

Критической точке на диаграмме состояния вещества соответствуют предельные точки на кривых равновесия фаз, в окрестностях точки фазовое равновесие нарушается, происходит потеря термодинамической устойчивости по плотности вещества. По одну сторону от критической точки вещество однородно (обычно при ), а по другую — разделяется на жидкость и пар.

В окрестностях точки наблюдаются критические явления: из-за роста характеристических размеров флуктуаций плотности резко усиливается рассеяние света при прохождении через вещество — при достижении размеров флуктуаций порядков сотен нанометров, т. е. длин волн света, вещество становится непрозрачным — наблюдается его критическая опалесценция. Рост флуктуаций приводит также к усилению поглощения звука и росту его дисперсии, изменению характера броуновского движения, аномалиям вязкости, теплопроводности, замедлению установления теплового равновесия и т. п.

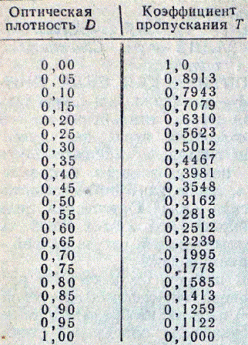
Задача №1. Коэффициент пропускания раствора т=0,3. Чему ровна его оптическая плотность?

оптическая плотность — мера поглощения света прозрачными объектами (такими, как фотоплёнка) или отражения света непрозрачными объектами (такими, как фотография).

Вычисляется как десятичный логарифм отношения потока излучения падающего на объект, к потоку излучения прошедшего через него (отразившегося), т. е. это есть логарифм от величины, обратной к коэффициенту пропускания (отражения).

К примеру D=4 означает, что свет был ослаблен в 104=10 000 раз, т. е. для человека это полностью чёрный объект, а D=0 означает, что свет прошёл (отразился) полностью.

В терминах оптической плотности задаются требования к выдержке негативов.

Прибор для измерения оптической плотности называется денситометром. В рентгеновских методах неразрушающего контроля оптическая плотность рентгеновского снимка является параметром оценки пригодности снимка к дальнейшей расшифровке. Допустимые значения оптической плотности в рентгеновских методах неразрушающего контроля регламентируются в соответствии с требованиями ГОСТ.

D=lg(1/3) (Fin и Fout и есть t)

D= 0,523 (вроде похоже)

Задача №2.Средняя мощность экспозиционной дозы облучения в рентгеновском кабинете равна 6,45*10^-12 Ки/Кг*с. Врач находиться в течении 5 часов в кабинете. Какого его доза облучения за 6 дней?

1,7*10^-2 Бк/Кг*с

1,7*60 (секунд) =102

102*60 (минут)=6120

6120*5 (часов)=30600

30600*6 (дней)=183600 (в наш период)

183600*10^-2=0.18*10⁴ Бк/Кг

0.18*10⁴ Бк/Кг

Экспозиционная доза (X). В качестве количественной меры рентгеновского и -излучения принято использовать во внесистемных единицах экспозиционную дозу, определяемую зарядом вторичных частиц (dQ), образующихся в массе вещества (dm) при полном торможении всех заряженных частиц :

X = dQ/dm

   Единица экспозиционной дозы - Рентген (Р). Рентген - это экспозиционная доза рентгеновского и -излучения, создающая в 1куб.см воздуха при температуре О°С и давлении 760 мм рт.ст. суммарный заряд ионов одного знака в одну электростатическую единицу количества электричества. Экспозиционной дозе 1 Р     соответствует 2.08·109 пар ионов (2.08·109 = 1/(4.8·10-10)). Если принять среднюю энергию образования 1 пары ионов в воздухе равной 33.85 эВ, то при экспозиционной дозе 1 Р одному кубическому сантиметру воздуха передается энергия, равная :     (2.08·109)·33.85·(1.6·10-12) = 0.113 эрг,     а одному грамму воздуха :     0.113/ возд = 0.113/0.001293 = 87.3 эрг.     Поглощение энергии ионизирующего излучения является первичным процессом, дающим начало последовательности физико-химических преобразований в облученной ткани, приводящей к наблюдаемому радиационному эффекту. Поэтому естественно сопоставить наблюдаемый эффект с количеством поглощенной энергии или поглощенной дозы.

Задача №3. Скорость течения воды в некотором сечении горизонтальной трубы V= 5cм/с. Найдите скорость течения в той части трубы, которые имеет вдвое меньший диаметр? Вдвое меньшую площадь поперечного сечения?

1.Жидкость в диапазоне реальных в практике давлений несжимаема и объёмный расход - Gv воды вошедшей в широкое сечение, при переходе на меньшее сечение остался неизменен и исходя из этого можно записать баланс объёмных расходов широкой части трубы - Gv1 и в узкой - Gv2 частях.R1 и R2 радиусы.V1 и V2 скорость течения воды. Gv1=Gv2 или Пи*R1²*V1=Пи*R2²*V2 или R1²*V1=R2²*V2, отсюда (R1/R2)²=V2/V1 или 2²=V2/V1 или V2/V1=4, отсюда V2=4*V1=4*0,05=0,2 м/с.

2.Выделим мысленно несколько сечений в трубе, площади которых обозначим S1 и S2. При стационар ном течении через любое поперечное сечение трубы за равные промежутки времени переносятся одинаковые объемы жидкости.

Пусть υ1 — скорость жидкости через сечение S1, υ2 — скорость жидкости через сечение S2. За время Δt объемы жидкостей, протекающих через эти сечения, будут равны:

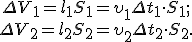
Так как жидкость несжимаема, то ΔV1 = ΔV2. Следовательно, υ1S1 = υ2S2 или υS = const для несжимаемой жидкости. Это соотношение называется уравнением неразрывности.

Из этого уравнения , т.е. скорости жидкости в двух любых сечениях обратно пропорциональны площадям сечений. Это значит, что частицы жидкости при переходе из широкой части трубы в узкую ускоряются.

V1/V2=0,5 или 0,05/V2=0,5 или V2=0,1 м/с