- •Глава 1. Функции и их свойства. 9
- •Глава 2. Влияние модуля на функции. 19
- •Глава 3. Функции вокруг нас. 21
- •Глава 1. Функции и их свойства.
- •1. Линейная функция.
- •1.2.Функция обратной пропорциональности.
- •Квадратичная функция.
- •1.5.Степенные функции.
- •1.7. Движение функций по осям координат.
- •Глава 2. Влияние модуля на функции.
- •Модуль в линейной функции.
- •2.2.Модуль и обратная пропорциональность.
1.5.Степенные функции.
Степенная
функция с натуральным показателем y= ,
где n
,
где n N
непрерывна на множестве действительных
чисел. Если n нечетное, то эта функция
строго возрастает и потому обратима.
Обратной к ней является функция y=
N
непрерывна на множестве действительных
чисел. Если n нечетное, то эта функция
строго возрастает и потому обратима.
Обратной к ней является функция y= .Степенная функция с четным показателем
необратима. Однако если сузить ее область
определения до области неотрицательных
чисел, то обратной к ней функцией также
будет y=
,
где x ≥ 0. На множестве (–∞; 0)
функцией, обратной к функции y=
(n – натуральное четное число) будет
y=
.Степенная функция с четным показателем
необратима. Однако если сузить ее область
определения до области неотрицательных
чисел, то обратной к ней функцией также
будет y=
,
где x ≥ 0. На множестве (–∞; 0)
функцией, обратной к функции y=
(n – натуральное четное число) будет
y=
 .
.
|
|
Рис 5.Степенная и обратная ей функции. |
Итак,
если x > 0, то при любом натуральном
n функция
![]() обратима,
а обратная к ней функция обозначается
как
или
обратима,
а обратная к ней функция обозначается
как
или
 .
Функция
.
Функция
 также определена и непрерывна на
множестве положительных чисел.
также определена и непрерывна на
множестве положительных чисел.
Свойства
функции y
=

D(f)=(
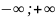 );
);Четная функция;
Убывает на луче (
 ;
возрастает на луче
;
возрастает на луче
 ;
;Ограничена снизу, не ограничена сверху;
=0, не существует;
Непрерывна;
E(f)=
 ;
;Выпукла вниз.
Свойства
функции y
=
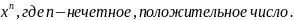
D(f)=( );
Нечетная функция;
Возрастает;
Не ограничена ни снизу, ни сверху;
Нет ни наибольшего, ни наименьшего значений;
Непрерывна;
E(f)=
 ;
;Выпукла вверх на (
 выпукла вниз на [0;
выпукла вниз на [0;
Свойства
функции y
=

D(f)=(
 )
)
 (0;
);
(0;
);Четная функция;
Убывает на открытом луче (0
 ;
возрастает на открытом луче
;
;
возрастает на открытом луче
;Ограничена снизу, не ограничена сверху;
Нет ни наибольшего, ни наименьшего значений;
Непрерывна при x
 и при x>0;
и при x>0;
E(f)= ;
Выпукла вниз и при x , и при x>0.
Свойства
функции y
=
D(f)=( ) (0; );
Нечетная функция;
Убывает на открытом луче (0 и на открытом луче ;
Не ограничена ни снизу, ни сверху;
Нет ни наибольшего, ни наименьшего значений;
Непрерывна при x и при x>0;
E(f)= ;
Выпукла вверх при x ; выпукла вниз при x>0.
1.6. Зависимость вида + = .
Графиком данного уравнения является окружность на координатной плоскости x Oy с центром в точке O(a;b) и радиусом r (r>0).
График данного уравнения нельзя назвать графиком функции, т.к. нарушается определение функции: каждому значению x соответствует единственное значение y.
1.7. Движение функций по осям координат.
Чтобы построить график функции y=f(x+l), где l – заданное положительное число, нужно сдвинуть график функции y=f(x) вдоль оси x на l единиц масштаба влево.
Чтобы построить график функции y=f(x-l), где l – заданное положительное число, нужно сдвинуть график функции y=f(x) вдоль оси x на l единиц масштаба вправо.
Чтобы построить график функции y=f(x)+m, где m – заданное положительное число, надо сдвинуть график функции y=f(x) вдоль оси y на m единиц масштаба вверх.
Чтобы построить график функции y=f(x)-m, где m - заданное положительное число, надо сдвинуть график функции y=f(x) вдоль оси y на m единиц масштаба вниз.
Алгоритм 1 построения графика функции y=f(x+l)+m:
Построить график функции y=f(x).
Осуществить параллельный перенос графика y=f(x) вдоль оси x на
 единиц масштаба влево, если l>0,
и вправо, если l<0.
единиц масштаба влево, если l>0,
и вправо, если l<0.Осуществить параллельный перенос полученного на втором шаге графика вдоль оси y на
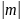 единиц масштаба вверх, если
единиц масштаба вверх, если

Алгоритм 2 построения графика функции y=f(x+l)+m:
Перейти к вспомогательной системе координат, проведя пунктиром вспомогательные прямые x=-l, y=m, т.е. выбрав в качестве начала новой системы координат точку (-l;m).
Новой системе координат привязать график функции y=f(x).
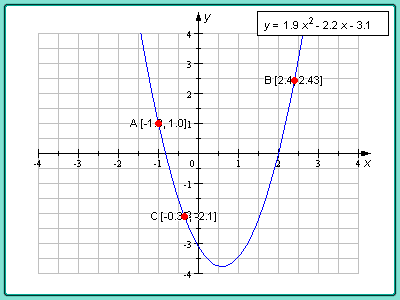
Рис
6. Функция у=1.9