2.2.1. Позиционные и непозиционные системы счисления
Системой счисления называется совокупность правил записи чисел с помощью заданного набора специальных знаков – цифр.
Системы счисления подразделяются на позиционные и непозиционные.
В настоящее время для представления чисел применяют главным образом позиционные системы счисления.
Позиционными называют системы счисления, в которых значение каждой цифры в изображении числа определяется ее положением (позицией) в ряду других цифр.
;
(2.1)
2.2.2. Двоичная и шестнадцатеричная системы счисления
Система счисления с основанием 2 называется двоичной. Цифрами двоичной системы являются 0 и 1. Интерес именно к этой системе счисления связан с тем, что любая информация в ЭВМ представляется в виде двух состояний, которые легко реализуются технически.
2.2.3. Перевод чисел из одной системы счисления в другую
Для перевода числа из любой системы счисления в десятичную систему можно воспользоваться представлением исходного числа как суммы произведений цифр данного числа и степеней основания исходной системы счисления. Алгоритм такого перевода выглядит следующим образом (действия проводятся в десятичной системе счисления):
1) цифры исходного числа нумеруются справа налево начиная с нуля – для целой части числа и слева направо начиная с -1 – для дробной части;
2) каждая цифра числа переводится в число в десятичной системе;
3) десятичное число, соответствующее каждой цифре, умножается на основание исходной системы счисления в пронумерованной степени, и результаты складываются.
Пример 2.1. Пусть требуется перевести двоичное число 111101,101(2) в десятичную систему счисления.
=
= 32 + 16 + 8 + 4 + 1 + 0,5 + 0,125 = 61,625(10).
Пример 2.2. Пусть требуется перевести шестнадцатеричное число 5A1,2С(16) в десятичную систему счисления.
5∙162 + А∙161 + 1∙160 + 2∙16–1 + С∙16–2 = 5∙256 + 10∙16 +
+ 1∙1 + 2∙0,0625 + 12∙0,00390625 = 1280 + 160 + 1 + 0,125 +
+ 0,046875 = 1441,171875(10).
Согласно этому алгоритму перевод числа, включающего в себя целую и дробную части, состоит из вычислительных процессов двух видов:
1) последовательного деления нацело целой части и образующихся целых частных на основание новой системы счисления;
2) последовательного умножения дробной части и дробных частей получающихся произведений на то же новое основание, записанное, как и в первом случае, цифрами исходной системы счисления.
При переводе целой части числа в ходе процесса последовательного деления получаются остатки, выраженные цифрами исходной системы счисления. Они представляют собой цифры a0, a1, …, an целой части числа, переведенного в новую систему счисления. Последний остаток является старшей цифрой переведенного числа. Процесс деления продолжается до тех пор, пока частное не станет равным нулю.
При переводе дробной части числа при каждом умножении получаются целые части, которые исключаются из последующих умножений. Эти целые части, изображенные цифрами исходной системы счисления, представляют собой цифры дробной части,
переведенной в новую систему счисления. Значение первой целой части является первой цифрой после запятой переведенного числа. Процесс умножения продолжаем до тех пор, пока дробная часть произведения не станет равной нулю или не выделится период.
Следует отметить, что все арифметические действия осуществляются по правилам исходной системы счисления.
Пример 2.3. Пусть требуется перевести десятичное число 30,6(10) в двоичную систему счисления.
Переводим отдельно целую и дробную части числа.
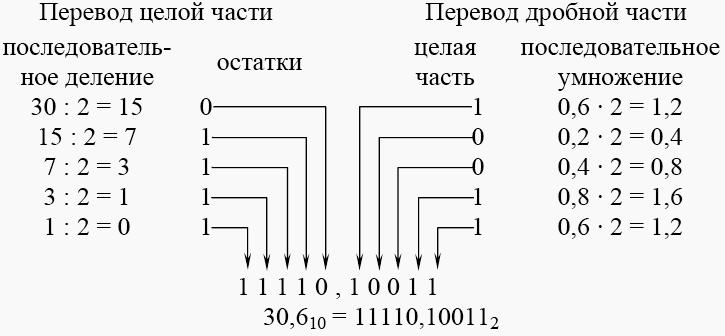
Пример 2.4. Пусть требуется перевести десятичное число 3149,76(10) в шестнадцатеричную систему счисления.
Переводим отдельно целую и дробную части числа.
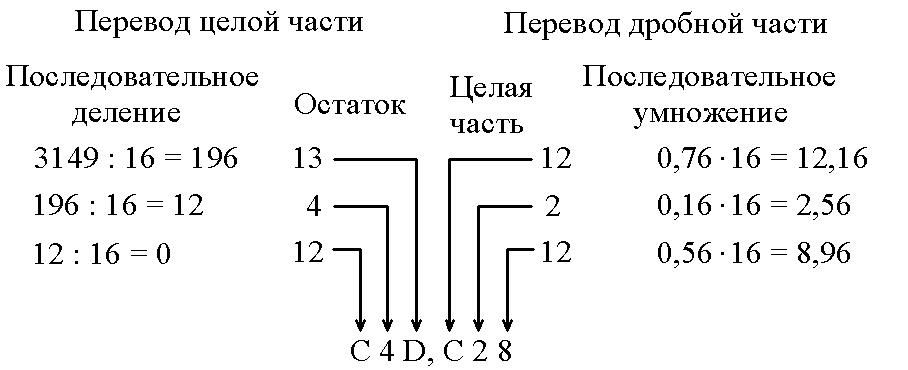
Таким образом, 3149,76(10) = C4D,C28(16).