
- •Уравнения максвела. Электромагнитные волны
- •1. Фарадеевская и максвелловская трактовки явления электромагнитной индукции. Ток смещения.
- •2. Система уравнений Максвелла в интегральной и дифференциальной формах. Электромагнитное поле.
- •3. Волновые уравнения для электромагнитного поля и их решения. Скорость распространения электромагнитных волн в средах. Основные свойства электромагнитных волн.
- •4. Энергия и поток энергии электромагнитных волн. Вектор Пойнтинга.
- •5. Изучение диполя. Диаграмма направленности.
- •Вопросы для самоконтроля.
- •Распространение света через границу двух сред
- •2. Полное внутреннее отражение. Световоды.
- •Геометрическая оптика как предельный случай волновой оптики.
- •Вопросы для самоконтроля.
- •Интерференция света
- •Интерференция света. Когерентность и монохроматичность
- •2. Пространственная когерентность. Радиус когерентности.
- •3. Оптическая длина пути. Расчет интерференционной картины о двух когерентных источников.
- •4. Полосы равной толщины и равного наклона.
- •Вопросы для самоконтроля.
- •Дифракция света
- •1. Дифракция света. Принцип Гюйгенса-Френеля.
- •2. Дифракция Фраунгофера на одной щели.
- •Вопросы для самоконтроля.
- •Поляризация света
- •1. Естественный и поляризованный свет. Виды поляризации. Степень поляризации.
- •Поляризация при отражении и преломлении. Закон Брюстера.
- •4. Поляроиды и поляризационные призмы. Поляризаторы и анализаторы.
- •5. Искусственная оптическая анизотропия. Эффект Керра.
- •6. Вращение плоскости поляризации.
- •Вопросы для самоконтроля.
- •Дисперсия света. Поглощение света.
- •Дисперсия света. Методы наблюдения дисперсии. Нормальная и
- •2. Электронная теория дисперсии.
- •Затруднения электромагнитной теории Максвелла.
- •Поглощение света, спектр поглощения. Цвета тел.
- •Вопросы для самоконтроля.
- •Спектр колебаний. Разложение фурье.
- •Спектр и спектрограмма функции.
- •Разложение Фурье. Понятие о гармониках.
- •Спектральное разложение несинусоидального периодического сигнала.
- •Вопросы для самоконтроля.
3. Волновые уравнения для электромагнитного поля и их решения. Скорость распространения электромагнитных волн в средах. Основные свойства электромагнитных волн.
Пусть имеется однородная и изотропная
среда вдали от зарядов и токов. Возбудим
в какой-либо точке пространства переменное
электрическое гармоническое поле
![]() (Предположим
(Предположим
![]() Для простоты рассматриваем этот частный
случай).
Для простоты рассматриваем этот частный
случай).
Из уравнений Максвелла при условии сделанных предположений можно получить волновые уравнения электромагнитного поля
= √ℰμℰ
μ
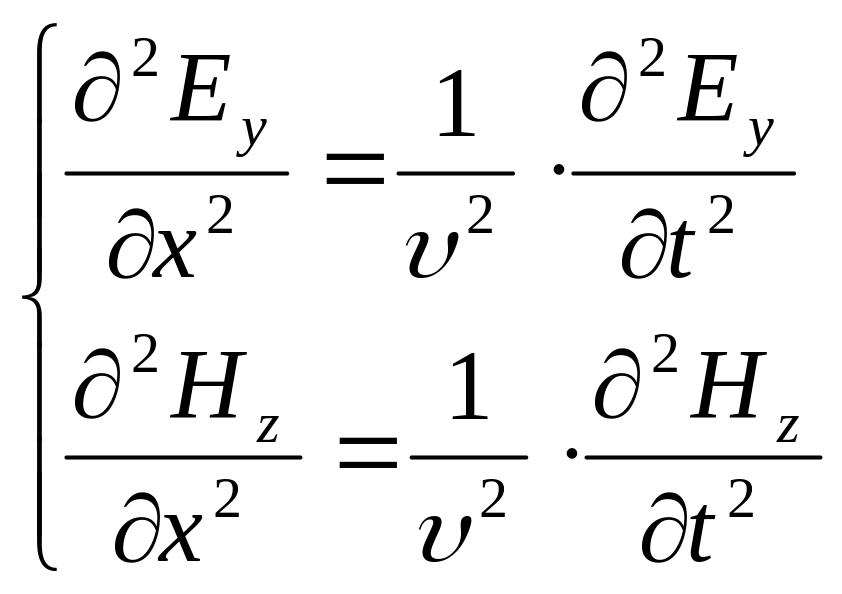
где - скорость распространения электро-
магнитной волны.
Процесс распространения электромагнитного поля в пространстве называется электромагнитной волной.
П![]() одставим
ℰ
= 8,85
одставим
ℰ
= 8,85![]() μ
=
μ
=
![]() в выражение для скорости .
Если среда – вакуум, то ℰ
= 1, μ = 1, тогда получим
= , то есть скорость
электромагнитной волны в вакууме равна
скорости света в вакууме. Это
обстоятельство приводит к выводу, что
свет - электромагнитная волна.
в выражение для скорости .
Если среда – вакуум, то ℰ
= 1, μ = 1, тогда получим
= , то есть скорость
электромагнитной волны в вакууме равна
скорости света в вакууме. Это
обстоятельство приводит к выводу, что
свет - электромагнитная волна.
Решения уравнений (30-14)
![]() (30-15)
(30-15)
Выражения (30-15) – уравнения электромагнитной волны. Их графическое
представление показано на рис. 30.5.
Электромагнитная волна является
поперечной волной, то есть колебания
векторов
и
происходят перпендикулярно направлению
распространения волны. Вектора
и
достигают максимума одновременно, но
колеблются в двух взаимно перпендикулярных
плоскостях.
Х
У
Z
Рис. 30.5










![]()
Как показывает опыт, электромагнитные волны проходят через диэлектрики и отражаются от металлов. Для них свойственны такие явления как интерференция, дифракция, поляризация, дисперсия (рассмотрим далее в разделе «Оптика»).
Итак, из решения уравнений Максвелла получаются следующие выводы:
– если в какой-либо ограниченной области пространства возникает электромагнитное поле, то оно не остается локализованным в этой области, а распространяется с конечной скоростью, зависящей от свойств среды;
– если электрическое и магнитные поля меняются по простому гармоническому закону, то электромагнитное поле распространяется в пространстве в виде плоской электромагнитной волны.
4. Энергия и поток энергии электромагнитных волн. Вектор Пойнтинга.
Поскольку и электрическое и магнитное
поля обладают определенной энергией,
то электромагнитная волна имеет
определенный запас энергии. Объемная
плотность электрического поля
![]() = ℰℰ
= ℰℰ
![]() /2,
магнитного поля
/2,
магнитного поля
![]() = μμ
= μμ
![]() /2.
Можно показать [ ], что вследствие
равноценности электрического и магнитного
полей
=
.
То есть
/2.
Можно показать [ ], что вследствие
равноценности электрического и магнитного
полей
=
.
То есть
ℰℰ /2= μμ /2.
Извлекая, квадратный корень из обеих частей, получим
√ℰℰ
![]() = √μμ
= √μμ
![]()
Плотность энергии электромагнитного поля складывается из составляющих
w = + = ℰℰ /2 + = μμ /2
![]()
![]()
Представляя ℰℰ ∙ /2 как ℰℰ ∙ ∙ ℰℰ ∙ /2 и μμ ∙ /2 как μμ ∙ ∙
![]() μμ
∙
/2,
получим
μμ
∙
/2,
получим
w = ℰℰ ∙ ∙ ℰℰ ∙ /2 + μμ ∙ ∙ μμ ∙ /2
У множим и разделим первое слагаемое на μμ ∙ , а второе на ℰℰ ∙
w = μμ ∙ ℰℰ ∙ /2 ∙ ℰℰ ∙ / μμ ∙ + ℰℰ ∙ μμ /2∙
∙ μμ ∙ / ℰℰ ∙
У читывая равенство (30-16), производим необходимые сокращения и в результате получим
w = ℰ∙ℰ ∙μ∙μ ∙ ∙
П
оскольку
1/ ℰ∙μ∙ℰ
∙μ
= - скорость
распространения электромагнитной волны
(см. (30-15)), то w =
1/ u ∙
.
Умножив найденное выражение для w
на скорость волны u,
получим модуль вектора плотности
потока энергии S
= w∙u
=
∙
.
Векторы
и
перпендикулярны и образуют с направлением
распространения волны правовинтовую
систему. Следовательно, вектор плотности
потока электромагнитной энергии можно
представить как векторное произведение
и
,
так как направление вектора
![]() совпадает с направлением переноса
энергии, а модуль этого вектора равен
.
Таким образом
совпадает с направлением переноса
энергии, а модуль этого вектора равен
.
Таким образом
![]()
(30-17)
Вектор
![]() называется вектором Пойнтинга. (Или
вектором Умова-Пойнтинга.) Общее
представление о потоке энергии в
пространстве впервые было введено
русским ученым Умовым в 1874 г. Поэтому
вектор потока энергии без конкретизации
ее физической природы называется
вектором Умова. Пойнтингом было получено
выражение (30-17).)
называется вектором Пойнтинга. (Или
вектором Умова-Пойнтинга.) Общее
представление о потоке энергии в
пространстве впервые было введено
русским ученым Умовым в 1874 г. Поэтому
вектор потока энергии без конкретизации
ее физической природы называется
вектором Умова. Пойнтингом было получено
выражение (30-17).)
Физический смысл вектора Пойнтинга – плотность потока электромагнитной энергии, распространяющейся вместе с волной, то есть количество энергии, проходящей за единицу времени через единицу площади, расположенной перпендикулярно к направлению распространения волны (рис. 30.6).




Рис. 30.6
