
- •!1.Модели представления ис.
- •!2. Особенности сертификации и стандартизации криптографических средств.
- •4) Разработка шифровальных средств и/или средств цифровой подписи, шифровальных средств для защиты электронных платежей с использованием пластиковых кредитных карточек и смарт-карт.
- •!3. Схемы, используемые при разработке алгоритмического и программного обеспечения машинного моделирования.
- •!4. Прямая и обратная теорема Шеннона.
- •!5. Основные понятия и определения теории восстановления.
- •!6. Сети с коммутацией каналов и сети с коммутацией пакетов.
- •!7. Обучение многослойной нейронной сети с помощью алгоритма обратного распространения.
- •!8. Способы устранения многозначности.
!8. Способы устранения многозначности.
Многозначность интерпретации — обычное явление в задачах распознавания. При понимании естественного языка серьезными проблемами становятся многозначность смысла слов, их подчиненности, порядка слов в предложении. Проблемы понимания смысла возникают в любой системе, взаимодействующей с пользователем на естественном языке. Распознавание графических образов также связано с решением проблемы многозначной интерпретации. При компьютерной обработке знаний многозначность необходимо устранять путем выбора правильной интерпретации, для чего разработаны специальные методы. Один из таких методов — метод релаксации, предназначенный для систематического устранения многозначности при интерпретации изображений.
Теория ограничений предлагает устранить многозадачность и выстроить приоритеты для задач. Эта простая рекомендация значительно увеличивает количество проектов, завершенных вовремя. Кроме того, за счет постоянной сфокусированности на одной задаче, она выполняется быстрее и соответственно все проекты также завершаются быстрее. А для организаций, работающих в условиях многопроектной среды, это означает увеличение прибыли.
Метод релаксации - приближенный метод решения систем линейных уравнений.
Система линейных уравнений
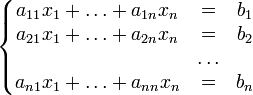 приводится
к виду
приводится
к виду
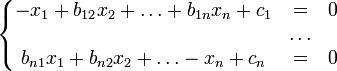
где
![]() ,
,
![]() ,
,
![]()
Находятся
невязки
Rj:
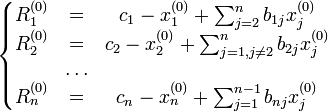
Выбирается
начальное приближениее X(0) =
0. На каждом шаге необходимо обратить в
ноль максимальную невязку:
![]() .
.
Условие
остановки:
![]() .
Ответ находится по формуле:
.
Ответ находится по формуле:
![]() .
.
