
В ариант 1.
А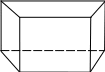 1.
A1
D
1.
A1
D
Основание призмы АВСDA1B1C1D1 – трапеция.
Какие из следующих пар прямых являются B1 C1 скрещивающимися? A
1) С1D и D1C 2) C1D и AB1 3) C1D и AB 4) AB и CD D1
B C
А2.
Укажите плоскость, параллельную прямой, D C
проходящей через точки пересечения B
д

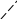
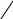

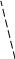
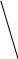
 иагоналей
граней AA1B1B
и BB1C1C
A
иагоналей
граней AA1B1B
и BB1C1C
A
параллелепипеда ABCDA1B1C1D1.
1) ADC1 2) DD1C1 3) CB1D1 4) AC1C1 D1 C1
A1 B1
А3.
О
 снование
призмы – правильный треугольник со
A1
B1
снование
призмы – правильный треугольник со
A1
B1
с тороной
6, а её боковое ребро равно 8
тороной
6, а её боковое ребро равно 8![]() и
и
наклонено к плоскости основания под углом 600. C1
Найдите объём призмы.
1) 36 2) 108 3) 108 4) 36




 A
B
A
B
K
C
А 4.
B1
C1
4.
B1
C1
Высота правильной четырёхугольной призмы
A


 BCDA1B1C1D1
равна 4
,
а сторона основания A1
BCDA1B1C1D1
равна 4
,
а сторона основания A1
– 4. Найдите расстояние между вершиной C и
т очкой
пересечения диагоналей боковой
очкой
пересечения диагоналей боковой
г


 рани
AA1B1B
C
рани
AA1B1B
C
1) 2![]() 2) 4
2) 4![]() 3) 4
4) 2
3) 4
4) 2
A D
А5.
Основание прямой призмы – прямоугольник со сторонами 4 и 3, а её высота равна 3. Найдите тангенс угла между диагональю призмы и плоскостью большей по площади боковой грани .
1)
![]() 2)
2)
![]() 3)
3)
![]() 4)
4)
![]()
В1.
Высота правильной
шестиугольной призмы равна 3, а площадь
основания -
![]() .
Найдите длину большей диагонали призмы.
.
Найдите длину большей диагонали призмы.
В2.
Высота правильной
четырёхугольной призмы ABCDA1B1C1D1
равна
![]() ,
а сторона основания -
,
а сторона основания -
![]() .
На продолжении бокового ребра BB1
за точку B1
отложен отрезок B1K,
равный ребру BB1.
Найдите площадь сечения, проходящего
через точки A,C
и K.
.
На продолжении бокового ребра BB1
за точку B1
отложен отрезок B1K,
равный ребру BB1.
Найдите площадь сечения, проходящего
через точки A,C
и K.
В3.
Сторона основания правильной четырёхугольной призмы ABCDA1B1C1D1 равна 8, а боковое ребро – 6. Точка К – середина отрезка ВС, точка О – середина отрезка СD1. Найдите объём многогранника AA1KO.
В4.
В правильной четырёхугольной призме боковое ребро равно стороне основания. Найдите угол между диагональю призмы и скрещивающейся с ней диагональю боковой грани.
