12. Примеры решения задач

Задача 1. Расстояние между пластинами плоского конденсатора составляет 5 мм. После зарядки конденсатора до разности потенциалов 500 В между пластинами конденсатора вдвинули стеклянную пластину (=7). Определите: 1)диэлектрическую восприимчивость стекла; 2) поверхностную плотность связанных зарядов на стеклянной пластине.

Дано	Решение
d=5 мм=510-3 м	Связь между диэлектрической восприимчивостью стекла и диэлектрической проницаемостью: . (1) Напряженность однородного электростатического поля в вакууме равна: . (2)
U=500 B
=7
Найти
 - ?
’-?

В диэлектрике напряженность электрического поля уменьшается в  раз, поэтому с учетом формулы (2) запишем:

. (3)

Поверхностная плотность связанных зарядов определяется поляризованностью диэлектрика, которая связана с напряженностью электростатического поля следующим образом:

,

с учетом формулы (3):

. (4)

Подставим числовые значения в формулы (1) и (4), выполним расчеты.

Ответ: ; .

Задача 2. Вблизи границы раздела стекло - вакуум (рис. 1) напряженность электрического поля в вакууме Е_о= 10 В/м, угол между вектором Е_о и нормалью n к границе раздела ₀ = 30⁰.

Найти напряженность Е₁ поля в стекле, угол ₁ между векторами Е₁ и n, а также поверхностную плотность связанных зарядов.

Дано	Решение
Ео= 10	Воспользуемся граничными условиями и , запишем выражения для нашего случая: , ; . Решая эти уравнения относительно Е1 и 1, получим: ; (1) . (2)
0 = 300 1=7
Найти Е1 -?
1-? ’- ?

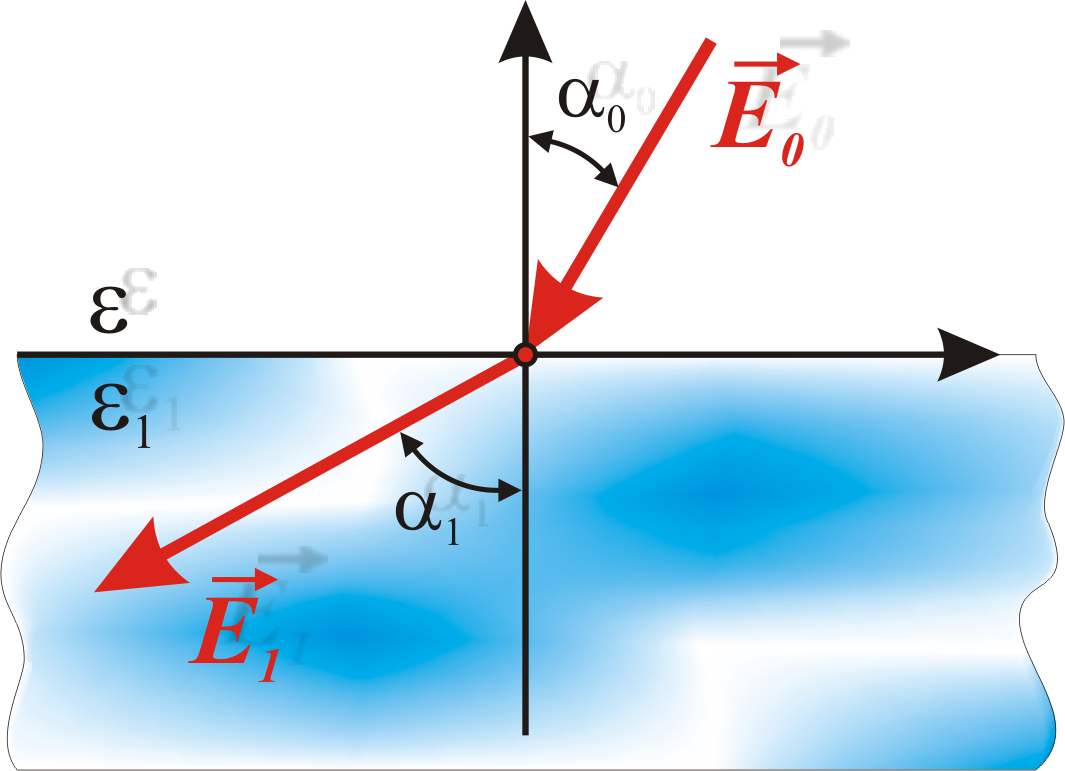
Рис.1 – Ход вектора напряженности на границе диэлектриков

Поверхностную плотность связанных зарядов найдем из условия (необходимо учесть, что поляризованность в вакууме равна нулю):

. (3)

Подставив в формулы (1), (2), (3) числовые значения, произведем вычисления.

Ответ: ; Е₁=5,16 ; ’=6,4510^-11 .

Задача 3. Пространство внутри плоского конденсатора заполнено двумя слоями диэлектриков, расположенными параллельно его обкладкам. Толщина слоев и диэлектрическая проницаемость материалов, из которых сделаны слои, соответственно равны l₁, l₂, ₁, ₂. Конденсатор заряжен до разности потенциалов U. Определить напряженности Е₁, Е₂ электрического поля в каждом из диэлектриков, а также напряженность Е₀ поля в зазоре, между обкладками и диэлектриками.

Дано	Решение
l1,	Чтобы найти величины Е1, Е2 и Е0, выясним связь, существующую между ними и разностью потенциалов U. Воспользуемся формулой , разобьем весь путь интегрирования на две части, соответствующие толщинам двух слоев диэлектриков (толщиной зазора пренебрегаем), и учитывая, что в пределах каждого слоя поле однородно, получим
l2,
1,
2
U
Найти
Е1-?
Е2-?
Е0-?

. (1)

Так как электрическое смещение D и в зазоре (=1), и в обоих слоях диэлектрика имеет одно и то же значение, то на основании формулы

запишем, сократив на ₀:

. (2)

Решая совместно уравнения (1) и (2), получим:

; ; .

Ответ: ; ; .

Задача 4. Бесконечно большая пластина из однородного диэлектрика с проницаемостью  заряжена равномерно зарядом с объемной плотностью . Толщина пластины 2d. Найти:

а) модуль напряженность электрического поля и потенциал как функции расстояния l от середины пластины (потенциал в центре пластины положить равным нулю).

б) поверхностную и объемную плотности связанного заряда.

Дано	Решение
	Найдем вначале напряженность электрического поля Еi внутри пластины. Воспользуемся теоремой Гаусса для вектора электрического смещения D.
2d
Найти
;
;
;

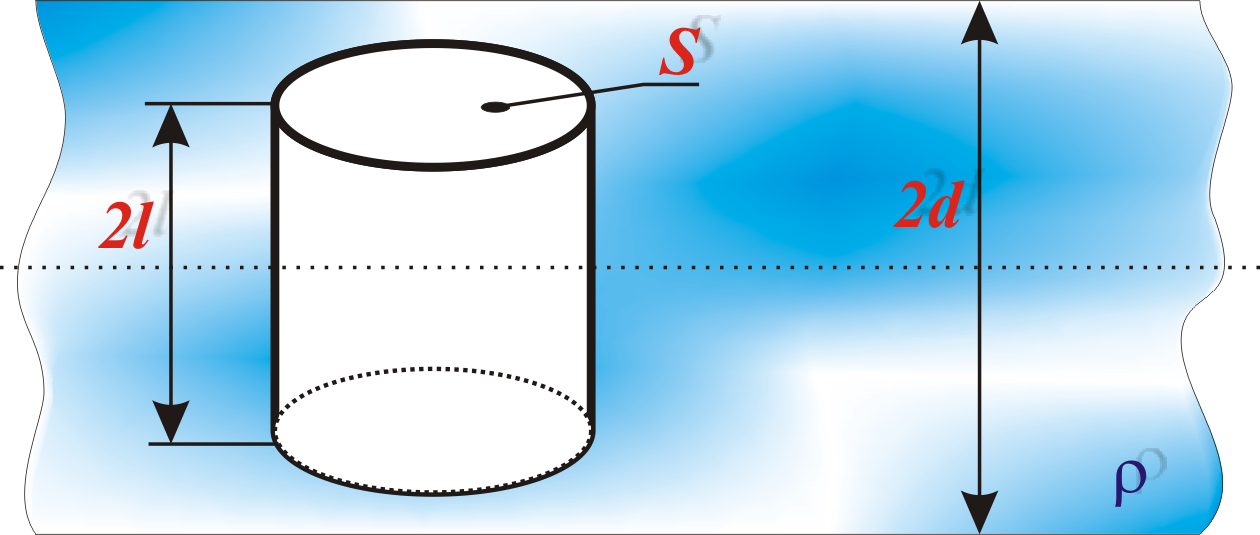
Рис.2 – Применение теоремы Гаусса для расчета D в диэлектрике

В качестве замкнутой поверхности выберем цилиндр с основаниями площади S, параллельными плоскости симметрии пластины, расположенный симметрично относительно этой плоскости, рис.2. Пусть высота цилиндра равна 2l (l<d).

Имеем:

откуда

.

С учетом получаем

.

Напряженность поля вне пластины Е_е найдем, воспользовавшись тем же принципом, только выбрав в качестве замкнутой поверхности цилиндр с l > d:

Используем теорему Остроградского-Гаусса для расчета электростатических полей:

.

Тогда

.

Отсюда

.

С учетом того, что потенциал в центре пластины равен нулю, потенциал в точке l равен

,

найдем

, .

Для определения плотностей связанного заряда найдем поляризованность внутри пластины:

.

Отсюда, используя формулу

,

найдем объемную плотность связанного заряда:

.

Поверхностная плотность связанного заряда определяется поляризованностью P_i у границы пластины: , тогда

.

Ответ: ; ;

; ;

; .

Задача 5. Свободные заряды равномерно распределены с объемной плотностью =5 по шару радиусом R=10 см из однородного, изотропного диэлектрика с проницаемостью =5. Определите напряженность электростатического поля на расстояниях r₁=5 cм и r₂=15 см от центра шара.

Дано	Решение
=5	Воспользуемся теоремой Гаусса для потока вектора электрического смещения D. . 1. Найдем D при r1  R (рис.3). , ,
R=10 см
=5
r1=5 cм
r2=15 см
Найти
Е1-?
Е2-?

откуда

.

Учитывая взаимосвязь между векторами D и E

,

перейдем в вектору Е:

.

Рис.3 – Применение теоремы Гаусса к расчету

электростатического поля диэлектрика.

2. Найдем D при r₂  R (рис.3). Согласно теореме Гаусса о потоке вектора электрического смещения:

,

откуда

.

,

поэтому

.

Проведя вычисления, получим: ; .

Ответ: 1,88 ; 8,37 .