Тепловые действия тока

1. Нагревание током. Закон Джоуля-Ленца

Исследуя на опыте нагревание проводников током, Эмилий Христианович Ленц, член Российской Академии наук (1804-1865) и Джеймс Джоуль, английский физик (1818-1889) установили, что количество тепла, выделяющееся в проводнике при прохождении через него электрического тока, прямо пропорционально сопротивлению R проводника, квадрату величины тока I и времени t, в течение которого поддерживается ток в проводнике. Этот закон, носящий название закона Джоуля-Ленца, можно выразить следующей формулой:

, (1)

где Q – выделившееся количество тепла.

Пользуясь законом Ома, можно выразить величину тока I через напряжение U на концах проводника и его сопротивление R. Подставив в формулу (1) найдем:

. (2)

Формулы (1) и (2), позволяют рассчитать количество тепла, выделяющегося в отдельных проводниках, соединенных последовательно и параллельно. При последовательном соединении во всех проводниках течет ток одной и той же величины. Поэтому для сравнения количества тепла, выделяющегося в последовательно соединенных проводниках, удобнее формула (1). Она показывает, что при последовательном соединении нескольких проводников в каждом выделяется количество тепла, прямо пропорциональное сопротивлению проводника. При параллельном соединении ток в проводниках различен, но напряжение на их концах имеет одно и то же значение. Поэтому удобно пользоваться формулой (2). Она показывает, что при параллельном соединении в каждом проводнике выделяется количество тепла обратно пропорциональное сопротивлению проводника.

2. Работа и мощность тока

При протекании тока через цепь кроме нагревания проводников, могут иметь место химические изменения в них (в проводниках второго класса), может происходить перемещение магнитной стрелки, представляющем собой простейшую форму мотора, т.е. совершается механическая работа при помощи электрического тока.

В опытах Джоуля и Ленца ток проходил через неподвижные металлические проводники, поэтому единственным результатом работы тока было нагревание этих проводников и, следовательно, вся работа, совершенная током, шла на выделение тепла.

Вычислим работу, совершаемую электрическими силами при прохождении тока через участок цепи.

Рассмотрим однородный проводник, к концам которого приложено напряжение U. За время dt через сечение проводника переносится заряд dq = I dt. Так как ток представляет собой перемещение заряда dq под действием электрического поля, то, работа тока:

dA = Udq = IUdt. (3)

Если сопротивление проводника R, то, используя закон Ома, получим

. (4)

Из (3) и (4) следует, что мощность тока

. (5)

Если сила тока выражается в амперах, напряжение — в вольтах, сопротивление — в омах, то работа тока выражается в джоулях, а мощность — в ваттах. На практике применяются также внесистемные единицы работы тока: ваттчас (Втч) и киловатт-час (кВтч). 1 Втч— работа тока мощностью в 1 Вт в течение 1 ч: 1 Втч=3600Втс=3,610³Дж; 1кВтч=10³Втч=3,610⁶ Дж.

Если ток проходит по неподвижному металлическому проводнику, то вся работа тока идет на его нагревание и, по закону сохранения энергии,

dQ = dA. (6)

Таким образом, используя выражения (6), (3) и (4), получим

dQ=IUdt =I²Rt = . (7)

Выражение (7) представляет собой закон Джоуля — Ленца, полученный теоретическим путем.

Выделим в проводнике элементарный цилиндрический объем dV=dSdl (ось цилиндра совпадает с направлением тока), сопротивление которого

.

По закону Джоуля - Ленца, за время dt в этом объеме выделится теплота.

.

Количество теплоты, выделяющееся за единицу времени в единице объема, называется удельной тепловой мощностью тока. Она равна

. (8)

Используя дифференциальную форму закона Ома и соотношение , получим

. (9)

Формулы (8) и (9) являются обобщенным выражением закона Джоуля - Ленца в дифференциальной форме, пригодным для любого проводника.

Тепловое действие тока находит широкое применение в технике, которое началось с открытия в 1873 г. русским инженером А. Н. Лодыгиным (1847—1923) лампы накаливания. На нагревании проводников электрическим током основано действие электрических муфельных печей, электрической дуги (открыта русским инженером В. В. Петровым(1761-1834)), контактной электросварки, бытовых электронагревательных приборов и т. д.

Рассмотрим принцип работы контактной сварки. Если сопротивление какого-либо участка цепи значительно больше, чем сопротивление всех остальных участков, то здесь выделяется практически все джоулево тепло. Такой случай осуществляется и в лампах накаливания и в нагревательных приборах, сопротивление которых значительно больше, чем сопротивление подводящих проводов. Таким же распределением сопротивлений пользуются при так называемой контактной электросварке, применяемой для металлов со значительными удельными сопротивлениями (никель, тантал, молибден и др.). Свариваемые пластины помещаются обычно между толстой медной пластиной и медным стержнем большого поперечного сечения. В этом случае все сопротивление участка практически сосредоточено в месте контакта свариваемых деталей: во-первых, материал этих деталей имеет большое удельное сопротивление, и, во-вторых, место соприкосновения (контакт) представляет большое сопротивление. При больших токах (употребляют сотни и тысячи ампер) детали раскаливаются добела и свариваются, в то время как медные электроды почти не нагреваются.

Примеры решения задач

Задача 1. Сила тока в проводнике сопротивлением R=120 Ом равномерно возрастает от I₀=0 A до I_max=5A за время =15 с. Определите выделившееся за это время в проводнике количество теплоты.

Дано	Решение
R=120 Ом	Запишем закон Джоуля-Ленца: , (1) Установим закон возрастания силы тока со временем. Сила тока возрастала равномерно, следовательно, изменение описывается линейной зависимостью. , (2) где k – коэффициент равный: . (3)
I0=0 A
Imax=5A
=15 с
Q - ?

Подставим формулы (2) и (3) в (1) и возьмем интеграл от полученного выражения:

.

Подставим числовые значения и произведем вычисления:

Q=15 кДж.

Ответ: 15 кДж.

Задача 2. От источника, разность потенциалов на клеммах которого U₀=10⁵ В, требуется передать мощность N=510³ кВт на расстояние l=5 км. Допустимая «потеря» напряжения в проводах n=1. Рассчитайте минимальное сечение S медного провода, пригодного для этой цели.

Дано	Решение
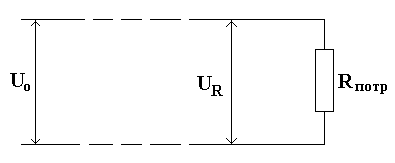
U0=105 В	Выполним чертеж (рис.1). Рис.1- Схематический чертеж к задаче Здесь U0 – разность потенциалов на клеммах источника, Rпотр – нагрузка потребителя, UR – напряжение на нагрузке. Напряжение источника частично падает на подводящих
N=5106 Вт
l=5 км
n=1
=1,710-6 Омм
S - ?

проводах и частично подается потребителю:

.

Ток на нагрузке и в проводах один и тот же, так как и нагрузка и провода соединены последовательно. Он может быть определен из соотношения:

; . (1)

«Потеря напряжения» в проводах с одной стороны может быть найдена из условия задачи, с другой стороны по закону Ома. Тогда:

. (2)

Сопротивление проводов R может быть выражено через длину и сечение одного провода:

. (3)

Длина проводов берется 2l, так как для передачи мощности на расстояние l используются два провода.

Подставив формулы (1) и (3) в (2), получим:

,

откуда

.

Подставим численные значения и произведем расчет:

S=8,510^-6 м².

Ответ: 8,510^-6 м².

Задача 3. Э.д.с. батареи Е=12 В. Наибольшая сила тока которую может дать батарея, I_max=5,0 А. Какая наибольшая мощность Р может выделиться на подключенном к батареи резисторе с переменным сопротивлением?

Дано	Решение
Е=12 В	Мощность Р тока измеряется работой, совершенной электрическими силами в единицу времени. Поскольку вся работа на внешнем участке цепи идет на нагревание резистора, то в данном случае мощность измеряется количеством теплоты, выделяемым в резисторе в единицу времени.
Imax=5,0 А
Q - ?

. (1)

По закону Ома для замкнутой цепи:

. (2)

где R и r - сопротивления внешнего и внутреннего участков цепи соответственно.

Подставим формулу (2) в (1):

. (3)

Проанализировав формулу (3), можно заметить, что при постоянных величинах Е и r мощность Р является функцией одной переменной - внешнего сопротивления R.

Для того, чтобы определить при каком R, мощность приобретает максимальное значение возьмем производную Р по внешнему сопротивлению R.

,

откуда

.

По условию максимума требуется равенство нулю первой производной:

, откуда R=r. (4)

Можно убедиться, что при этом условии мы имеем максимум, а не минимум мощности, определив знак второй производной.

Таким образом, мощность достигает максимального значения, когда внешнее сопротивление цепи равно внутреннему.

Используя условие (4) в выражении (3), получим:

. (5)

Таким образом, задача сводится к отысканию сопротивления r внутреннего участка цепи (батареи). Если учесть, что согласно закону Ома для замкнутой цепи наибольшая сила тока будет при внешнем сопротивлении равном нулю (ток короткого замыкании), то

. (6)

Подставив найденное из (6) значение внутреннего сопротивления r в формулу (5), получим

.

Подставив численные значения и произведя вычисления, получим:

Р =15 Вт.

Ответ: 15 Вт.