
3. Распределение 60 банков по величине процентной ставки X (%) и размеру выданных кредитов y (млн. Руб.) представлено в таблице.
У X |
2-5 |
5-8 |
8-11 |
11-14 |
14-17 |
Итого |
11-13 |
|
|
|
1 |
6 |
7 |
13-15 |
|
|
4 |
7 |
3 |
14 |
15-17 |
|
1 |
11 |
5 |
1 |
18 |
17-19 |
4 |
5 |
2 |
|
|
11 |
19-21 |
8 |
2 |
|
|
|
10 |
Итого |
12 |
8 |
17 |
13 |
10 |
60 |
Необходимо:
1.
Вычислить
групповые средние
![]() и
и
![]() ,
и
построить
эмпирические
линии регрессии.
,
и
построить
эмпирические
линии регрессии.
2. Предполагая, что между переменными X и Yсуществует линейная корреляционная зависимость:
а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений;
б) вычислить коэффициент корреляции; на уровне значимости
α = 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными Х и Y;
в) используя соответствующее уравнение регрессии, определить средний размер выданного банком кредита, процентная ставка которого равна 16%.
Решение:
Вычислим групповые средние и , построим эмпирические линии регрессии.
Для
каждого значения
![]() ,
т.е. для каждой строки корреляционной
таблицы вычислим групповые средние
,
т.е. для каждой строки корреляционной
таблицы вычислим групповые средние
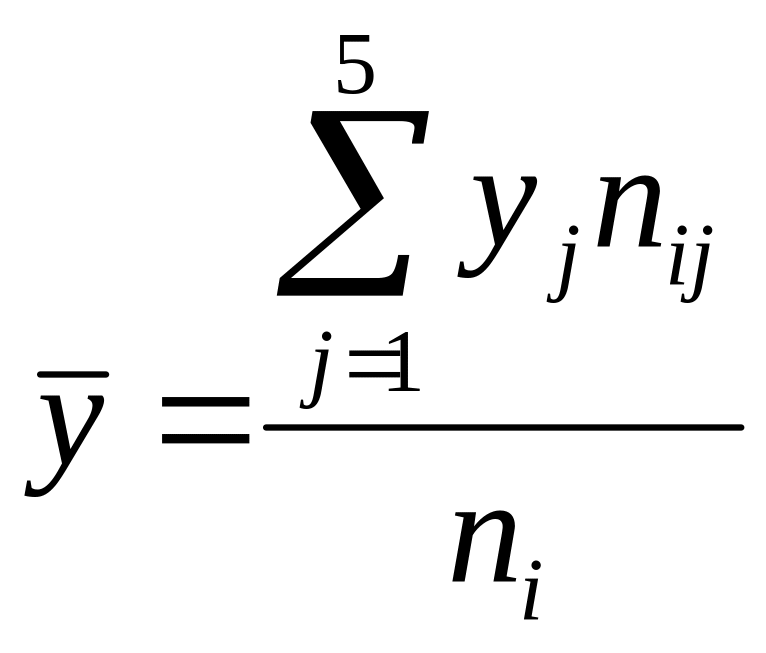 ,
где
,
где
![]() -
частоты пар (
-
частоты пар (![]() )
и
)
и
![]() .
.
Вычисленные
групповые средние
![]() поместим в последнем столбце корреляционной
таблицы и изобразим графически в виде
ломаной, называемой эмпирической линией
регрессии Y
по X.
поместим в последнем столбце корреляционной
таблицы и изобразим графически в виде
ломаной, называемой эмпирической линией
регрессии Y
по X.
Аналогично
для каждого значения
![]() по формуле
по формуле
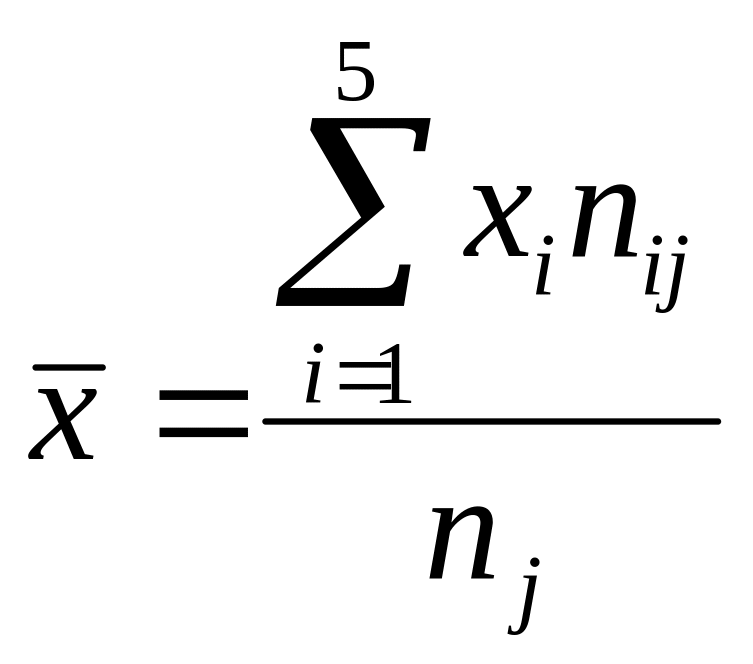 ,
где
-
частоты пар (
)
и
,
где
-
частоты пар (
)
и
![]() .
.
Вычисленные
групповые средние
![]() поместим в последней строке корреляционной
таблицы и изобразим графически в виде
ломаной, называемой эмпирической линией
регрессии X
по Y.
поместим в последней строке корреляционной
таблицы и изобразим графически в виде
ломаной, называемой эмпирической линией
регрессии X
по Y.
y x |
|
2-5 |
5-8 |
8-11 |
11-14 |
14-17 |
Итого: |
Группо вая сред няя, |
|
|
|
Сере дины интер валов |
3,5 |
6,5 |
9,5 |
12,5 |
15,5 |
||||
11-13 |
12 |
|
|
|
1 |
6 |
7 |
18,36 |
84 |
1008 |
13-15 |
14 |
|
|
4 |
7 |
3 |
14 |
22,04 |
196 |
2744 |
15-17 |
16 |
|
1 |
11 |
5 |
1 |
18 |
25,50 |
288 |
4608 |
17-19 |
18 |
4 |
5 |
2 |
|
|
11 |
30,50 |
198 |
3564 |
19-21 |
20 |
8 |
2 |
|
|
|
10 |
32,72 |
200 |
4000 |
Итого: |
12 |
8 |
17 |
13 |
10 |
60 |
|
966 |
15924 |
|
Групповая средняя,
|
50,14 |
59,67 |
72,11 |
85,57 |
96,11 |
|
|
|
|
|
|
42 |
52 |
162 |
163 |
155 |
573 |
|
|
|
|
|
147 |
338 |
1534,3 |
2031,3 |
2402,5 |
6453 |
|
|
|
|
Где,
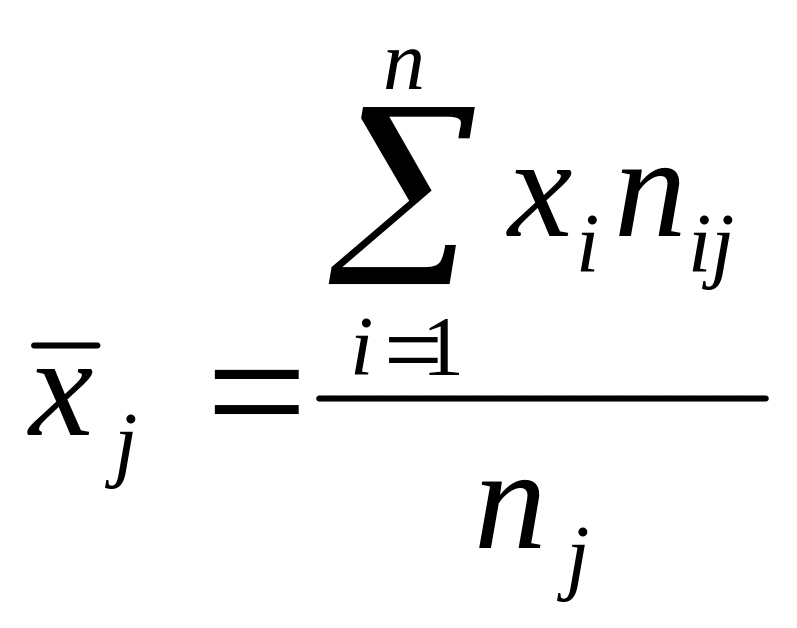 ,
,
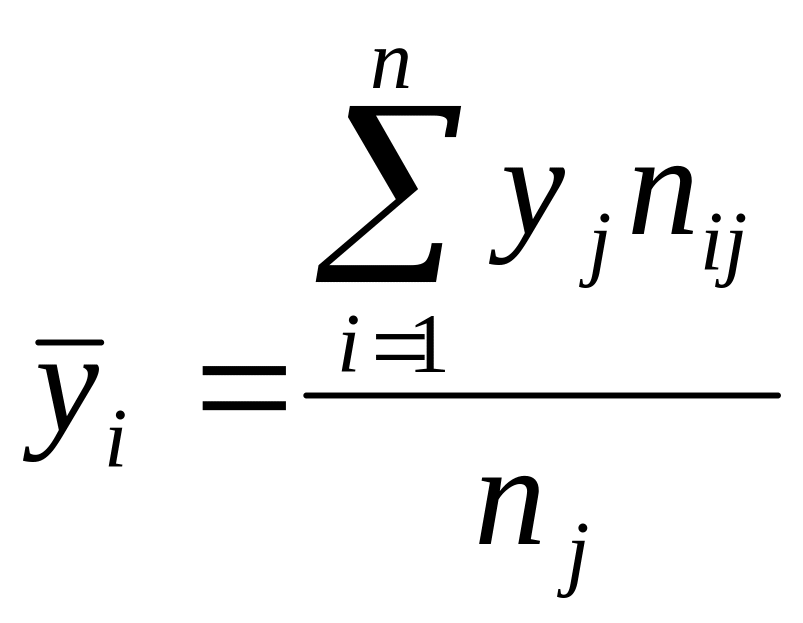 .
.
Эмпирическая линия регрессии Y по X:
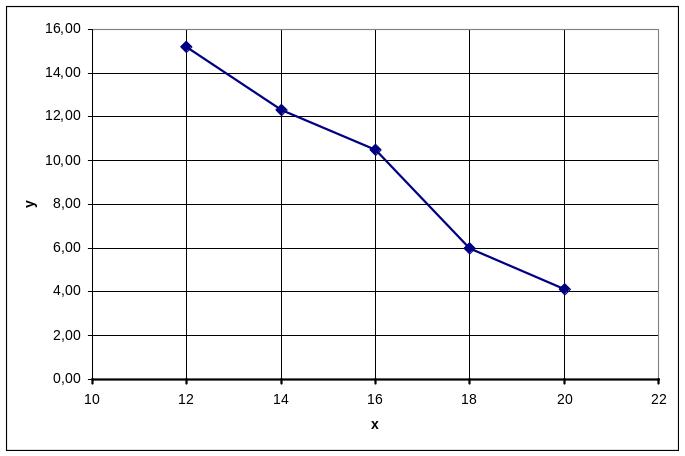
Эмпирическая линия регрессии X по Y:
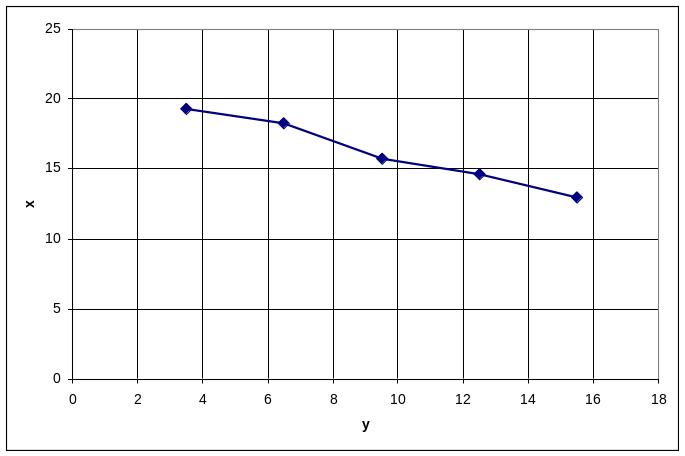
2) Предполагая, что между переменными Х и У существует линейная корреляционная зависимость: а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений;
Вычислим необходимые суммы:
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]()
Итак,
уравнение регрессии Y
по X:
![]() .
.
![]() ;
;
![]() .
.
Итак,
уравнение регрессии X
по Y:
![]() .
.
![]() ;
;
![]() .
.
Из первого уравнения регрессии Y по X следует, что при увеличении процентной ставки на 1 % размер выданных кредитов уменьшается на 1,422 млн. руб.
Из второго уравнения регрессии X по Y следует, что при увеличении выданных кредитов на 1 млн. руб. уменьшается процентная ставка на 0,539%.
Построим графики уравнений регрессии на одном чертеже с эмпирическими линиями регрессии:
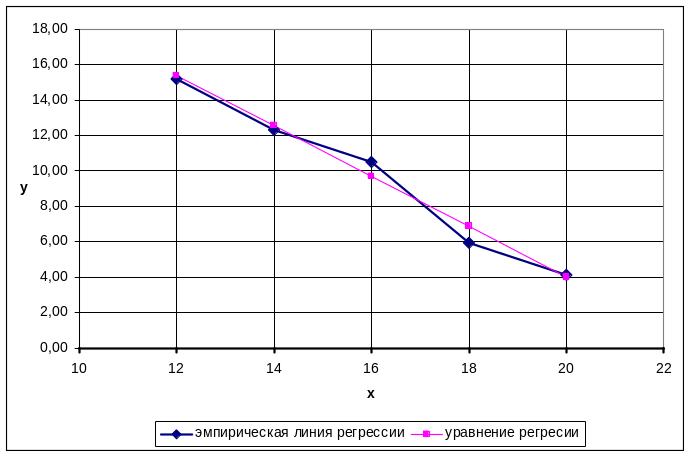
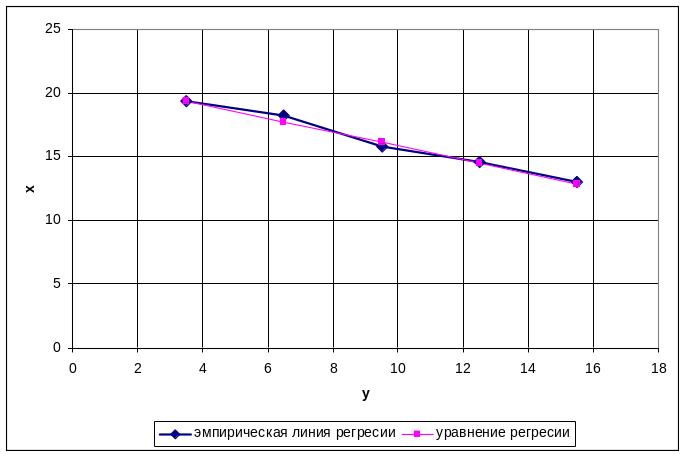
б) вычислить коэффициент корреляции, на уровне = 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными Х и У.
Вычислим коэффициент корреляции по формуле:
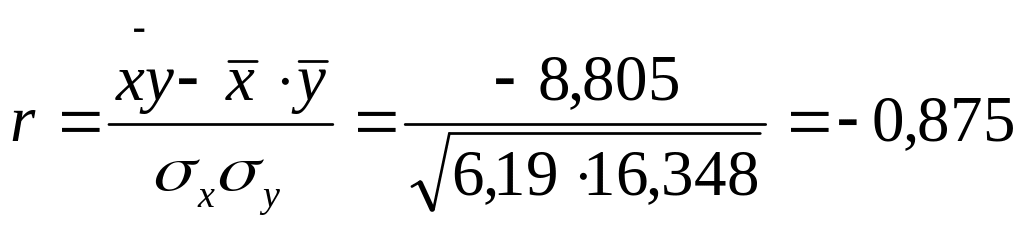 .
.
Связь
между переменными Х и У обратная, т.к.
![]() и достаточно
тесная (
и достаточно
тесная (![]() достаточно близок к 1).
достаточно близок к 1).
На уровне значимости = 0,05 оценить значимость коэффициента корреляции.
Нулевая
гипотеза
![]() ;
конкурирующая гипотеза
;
конкурирующая гипотеза
![]() .
.
Наблюдаемое значение критерия:
![]() .
.
По
уровню значимости
= 0,05 и числу степеней свободы
![]() находим по таблице
находим по таблице
![]() .
.
Поскольку
![]() - нулевую гипотезу отвергаем. Другими
словами, выборочный коэффициент
корреляции значимо отличается от нуля.
- нулевую гипотезу отвергаем. Другими
словами, выборочный коэффициент
корреляции значимо отличается от нуля.
в) используя соответствующее уравнение регрессии, определить средний размер выданного банком кредита, процентная ставка которого равна 16%.
Подставим
в уравнение регрессии
;
![]()
![]() млн. руб. –
средний размер выданного банком кредита.
млн. руб. –
средний размер выданного банком кредита.
