
Задача № 5
Плотность
вероятности нормально распределённой
случайной величины
имеет вид:
![]() .
Найти:
.
Найти:
а) математическое ожидание и среднее квадратическое отклонение случайной величины ;
б) вероятность
![]() ;
;
в) вероятность того, что отклонение случайной величины от её математического ожидания не превысит 2,5 (по абсолютной величине).
Решение.
а) Функция плотности вероятности
нормально распределённой случайной
величины
с математическим ожиданием
![]() и средним квадратическим отклонением
и средним квадратическим отклонением
![]() имеет вид:
имеет вид:
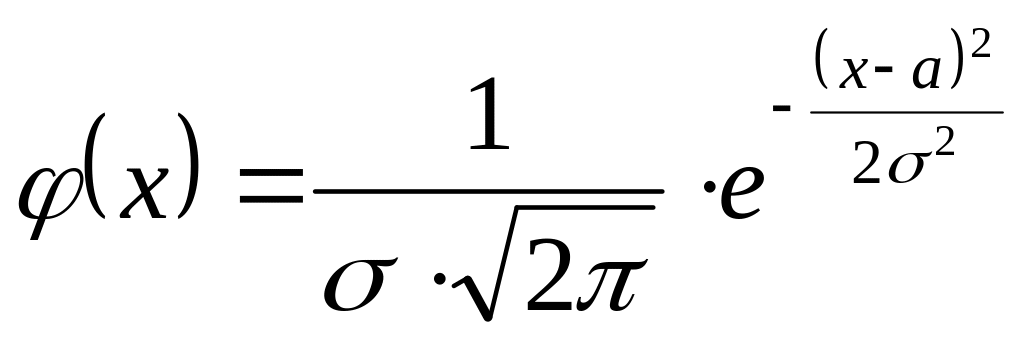 .
.
В нашем случае функция плотности
вероятности
,
следовательно, заданная случайная
величина
имеет нормальное распределение с
параметрами
![]() и
и
![]() .
Таким образом, для заданной случайной
величины
математическое ожидание
.
Таким образом, для заданной случайной
величины
математическое ожидание
![]() ,
а среднее квадратическое отклонение
,
а среднее квадратическое отклонение
![]() .
.
б) Найдём
вероятность того, что
примет значение в промежутке от
![]() до 0.
до 0.
Вероятность попадания в заданный
интервал
![]() нормально распределённой случайной
величины
вычисляется по формуле:
нормально распределённой случайной
величины
вычисляется по формуле:
![]() ,
,
где
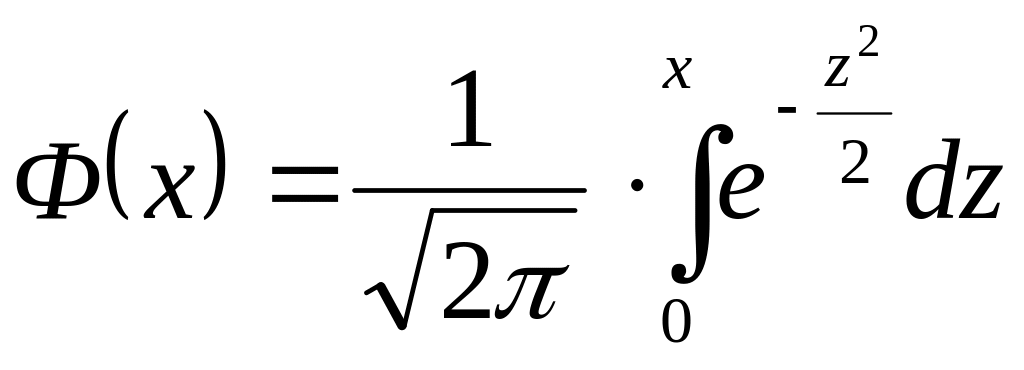 – функция Лапласа,
– функция Лапласа,
![]() – математическое ожидание случайной
величины
;
– математическое ожидание случайной
величины
;
![]() – среднее квадратическое отклонение.
– среднее квадратическое отклонение.
![]() .
.
По таблице значений функции Лапласа
находим:
![]() ,
,
![]() .
.
Значит вероятность того, что примет значение в промежутке от до 0:
![]() .
.
в) Вероятность заданного отклонения нормально распределённой случайной величины
вычисляется по формуле:
![]() ,
где
,
где
![]() – функция Лапласа.
– функция Лапласа.
Значит, вероятность того, что
отклонится (по модулю) от математического
ожидания
![]() не боле, чем на
не боле, чем на
![]() :
:
![]() .
.
По таблице значений функции Лапласа
находим:
![]() .
.
Следовательно, вероятность того, что
отклонение случайной величины
от её математического ожидания не
превысит 2,5 (по абсолютной величине)
![]() .
.
Ответ:
а)
![]() ,
,
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Контрольная работа №4 Вариант 6 продаётся!
Цена 500р. (качество работы – 100%, аналогично качеству данной кр. №3)
Для покупки обращайтесь к администрации
ВЗФЭИ-АРХИВа по адресу:
vzfeiextra@ya.ru
Способы оплаты:


Наличными в офисе (г.Воронеж)
