3) Проверим свойство математического ожидания . Вычислим математическое ожидание случайной величины .

			…
			…

Математическое ожидание дискретной случайной величины , закон распределения которой имеет вид , вычисляется по формуле .

В нашем случае .

Аналогично, ;

.

Значит , то есть выполнено равенство .

				8	24	48
	0,15	0,12	0,03	0,07	0,28	0,35

Ответ: ; ;

.

Задача № 5

Плотность вероятности случайной величины имеет вид:

Найти: а) функцию распределения ;

б) математическое ожидание и дисперсию ;

в) вероятность .

Построить графики функций и .

С помощью неравенства Маркова оценить вероятности того, что случайная величина примет значения: а) больше 6; б) не больше 5/3.

Найти те же вероятности с помощью функции распределения и объяснить различие результатов.

Решение.

1. Найдём функцию распределения 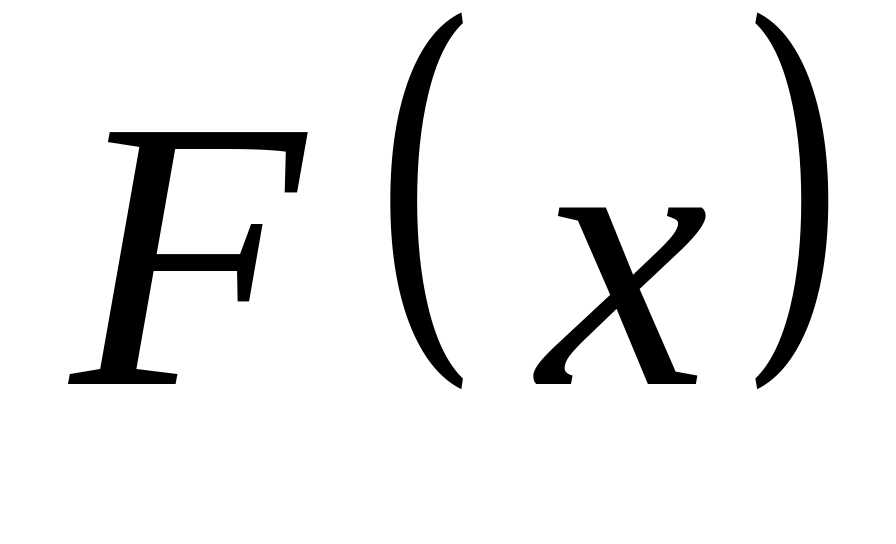случайной величины . Для этого воспользуемся формулой 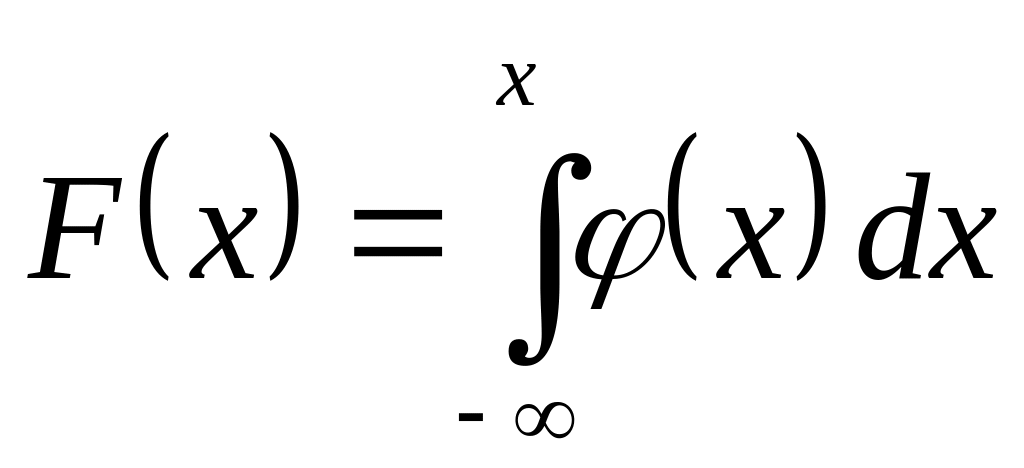, связывающей функцию распределения вероятностей с плотностью распределения вероятностей .

Для и .

Для

.

Для

.

Следовательно, функция распределения случайной величины имеет вид

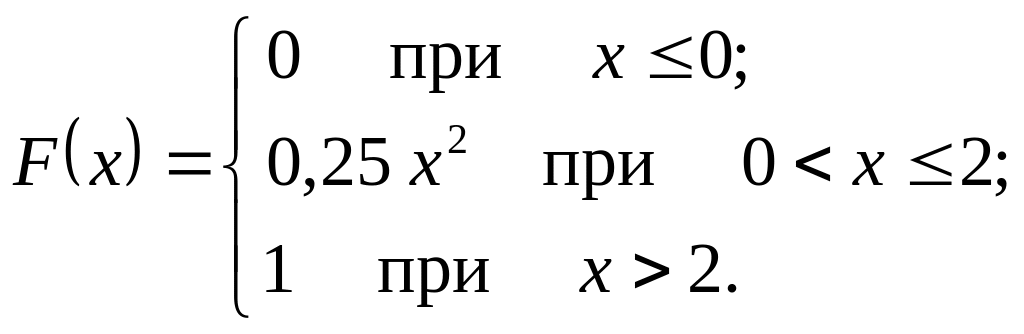
2. Математическое ожидание

.

Дисперсия .

.

Значит .

3. Определим вероятность того, что случайная величина примет значение из интервала 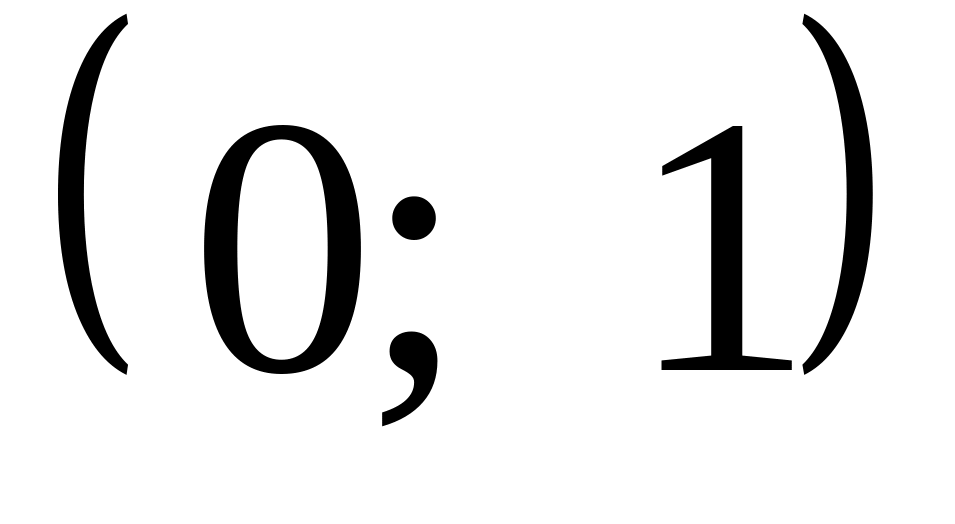с помощью функции распределения вероятностей :

.

4. Построим графики функций и .

График функции плотности распределения вероятностей случайной величины :

										3
										2
										1
		-4		-3		-2		-1		О		1		2		3		4		5			Х

График функции 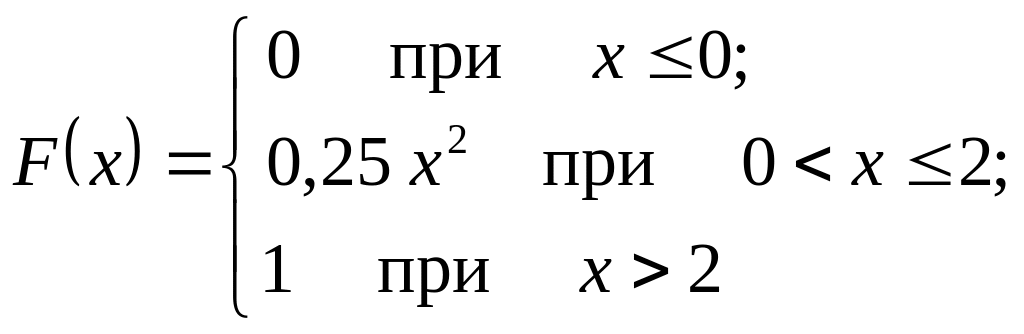распределения вероятностей случайной величины :

										3
										2
										1
		-4		-3		-2		-1		О		1		2		3		4		5		Х
										-1
										-2

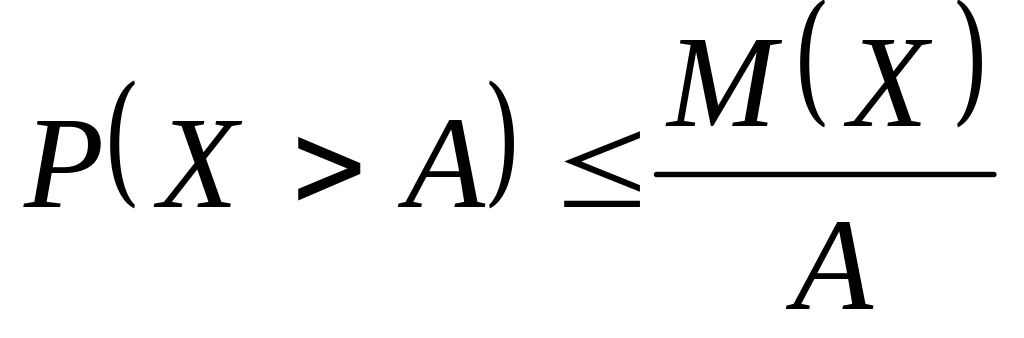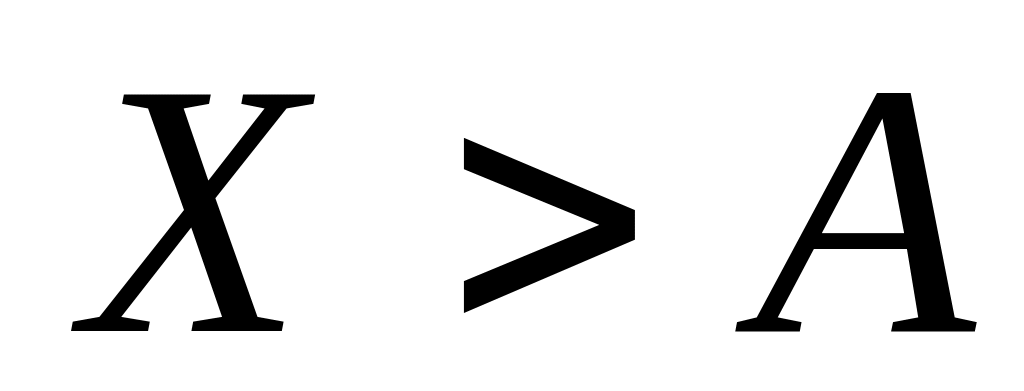5. Воспользуемся неравенством Маркова: если случайная величина принимает только неотрицательные значения и имеет математическое ожидание, то для любого положительного числа верно неравенство . Так как события и противоположные, можно получить другую форму неравенства Маркова: .

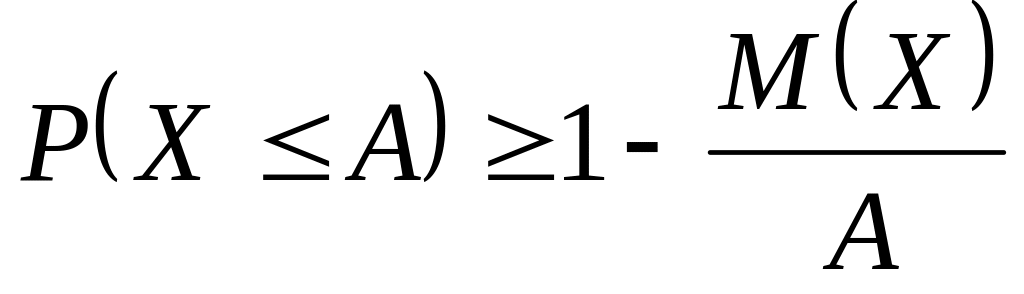а) Вероятность того, что случайная величина примет значение больше 6:

.

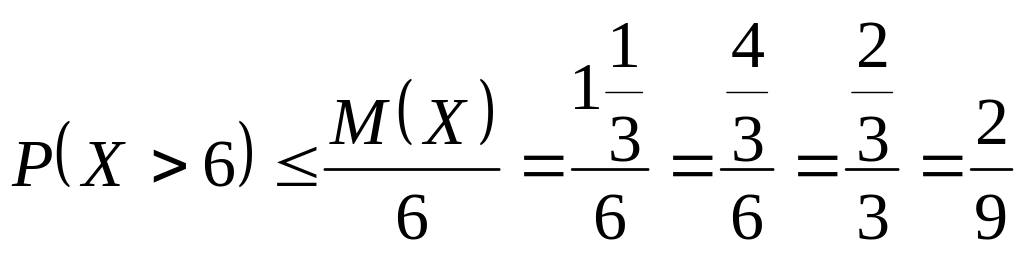б) Вероятность того, что случайная величина примет значение не больше 5/3 .

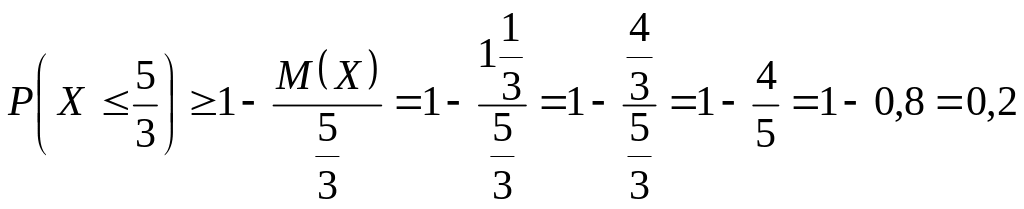Найдём те же вероятности с помощью функции распределения вероятностей :

;

.

Различие результатов обусловлено тем, что в первом случае мы получили оценку вероятности с помощью неравенства Маркова, а во втором случае вычислили точную вероятность с помощью функции распределения вероятностей.

Ответ: ; ; ;

; ; ; .

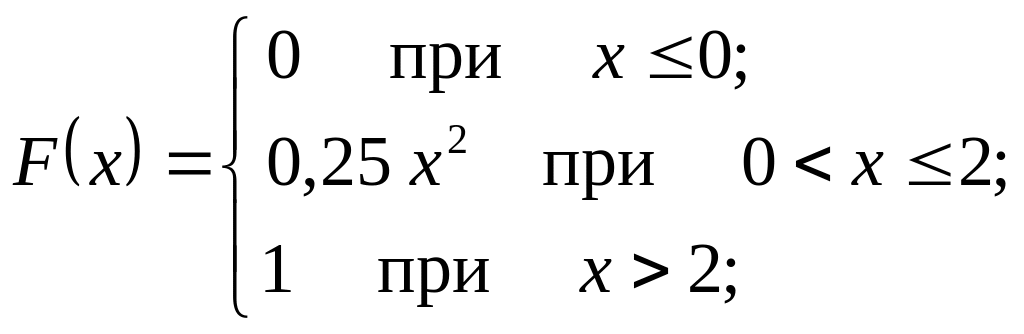
© ООО «ВЗФЭИ-АРХИВ.РФ», 2010 Страница 11